Tetrachords
According to the system of Aristoxenus and his followers—Cleonides, Bacchius, Gaudentius, Alypius, Bryennius, and Aristides Quintilianus[1]—the paradigmatic tetrachord was bounded by the fixed tones hypate and mese, which are a perfect fourth apart and do not vary from one genus to another. Between these are two movable notes, called parhypate and lichanos. The upper tone, lichanos, can vary over the range of a whole tone, whereas the lower note, parhypate, is restricted to the span of a quarter tone. However, their variation in position must always be proportional. This interval between the fixed hypate and movable parhypate cannot ever be larger than the interval between the two movable tones.[2] When the composite of the two smaller intervals is less than the remaining (incomposite) interval, the three-note group is called pyknon (meaning "compressed").
The positioning of these two notes defined three genera: the diatonic, chromatic (also called chroma, "colour"), and enharmonic (also called ἁρμονία [harmonia]). The first two of these were subject to further variation, called shades—χρόαι (chroai)—or species—εἶδη (eidē). For Aristoxenus himself, these shades were dynamic: that is, they were not fixed in an ordered scale, and the shades were flexible along a continuum within certain limits. Instead, they described characteristic functional progressions of intervals, which he called "roads" (ὁδοί), possessing different ascending and descending patterns while nevertheless remaining recognisable. For his successors, however, the genera became fixed intervallic successions, and their shades became precisely defined subcategories.[3][4] Furthermore, in sharp contrast to the Pythagoreans, Aristoxenos deliberately avoids numerical ratios. Instead, he defines a whole tone as the difference between a perfect fifth and a perfect fourth, and then divides that tone into semitones, third-tones, and quarter tones, to correspond to the diatonic, chromatic, and enharmonic genera, respectively.[5]
Diatonic
Aristoxenus describes the diatonic genus (Ancient Greek: διατονικὸν γένος) as the oldest and most natural of the genera.[6] It is the division of the tetrachord from which the modern diatonic scale evolved. The distinguishing characteristic of the diatonic genus is that its largest interval is about the size of a major second. The other two intervals vary according to the tunings of the various shades.
Etymology
The English word diatonic is ultimately from the Ancient Greek: διατονικός, romanized: diatonikós, itself from διάτονος, diátonos, of disputed etymology.
Most plausibly, it refers to the intervals being "stretched out" in that tuning, in contrast to the other two tunings, whose lower two intervals were referred to as πυκνόν, pyknón, from πυκνός, pyknós, 'dense, compressed'. This takes τόνος, tónos, to mean "interval of a tone"; see Liddell and Scott's Greek Lexicon Archived 2011-03-05 at the Wayback Machine and Barsky (second interpretation), below.
Alternatively, it could mean (as OED claims) "through the tones", interpreting διά, diá as "through". See also Barsky: "There are two possible ways of translating the Greek term 'diatonic': (1) 'running through tones', i.e. through the whole tones; or (2) a 'tensed' tetrachord filled up with the widest intervals".[7] The second interpretation would be justified by consideration of the pitches in the diatonic tetrachord, which are more equally distributed ("stretched out") than in the chromatic and enharmonic tetrachords, and are also the result of tighter stretching of the two variable strings. It is perhaps also sounder on linguistic morphological grounds.[8] Compare diameter as "across/width distance".
A completely separate explanation of the origins of the term diatonic appeals to the generation of the diatonic scale from "two tones": "Because the musical scale is based entirely on octaves and fifths, that is, two notes, it is called the 'diatonic scale' ".[9] But this ignores the fact that it is the element di- that means "two", not the element dia-, which has "through" among its meanings (see Liddell and Scott). There is a Greek term δίτονος, dítonos, which is applied to an interval equivalent to two tones. It yields the English words ditone and ditonic (see Pythagorean comma), but it is quite distinct from διάτονος.
The Byzantine theorist George Pachymeres consider the term derived from διατείνω, diateíno, meaning "to stretch to the end", because "...the voice is most stretched by it" (Medieval Greek: "... σφοδρότερον ἡ φωνὴ κατ’ αὐτὸ διατείνεται").[10][11]
Yet another derivation assumes the sense "through the tones" for διάτονος, but interprets tone as meaning individual note of the scale: "The word diatonic means 'through the tones' (i.e., through the tones of the key)" (Gehrkens, 1914, see Diatonic and chromatic § Diatonic includes the harmonic and melodic minor scales; see also the Prout citation, at the same location). This is not in accord with any accepted Greek meaning, and in Greek theory it would fail to exclude the other tetrachords.
The fact that τόνος itself has at least four distinct meanings in Greek theory of music contributes to the uncertainty of the exact meaning and derivation of διατονικός, even among ancient writers: τόνος may refer to a pitch, an interval, a "key" or register of the voice, or a mode.[12]
Shades or tunings
The diatonic tetrachord can be "tuned" using several shades or tunings. Aristoxenus (and Cleonides, following his example; see also Ptolemy's tunings) describes two shades of the diatonic, which he calls συντονόν (syntonón, from συντονός) and μαλακόν (malakón, from μαλακός).[13] Syntonón and malakón can be translated as "tense" ("taut") and "relaxed" ("lax, loose"), corresponding to the tension in the strings. These are often translated as "intense" and "soft", as in Harry Partch's influential Genesis of a Music, or alternatively as "sharp" (higher in pitch) and "soft" ("flat", lower in pitch). The structures of some of the most common tunings are the following:
The traditional Pythagorean tuning of the diatonic, also known as Ptolemy's ditonic diatonic, has two identical 9:8 tones (see major tone) in succession, making the other interval a Pythagorean limma (256:243):
hypate parhypate lichanos mese 4:3 81:64 9:8 1:1 | 256:243 | 9:8 | 9:8 | -498 -408 -204 0 cents
However, the most common tuning in practice from about the 4th century BC to the 2nd century AD appears to have been Archytas's diatonic, or Ptolemy's "tonic diatonic", which has an 8:7 tone (see septimal whole tone) and the superparticular 28:27 instead of the complex 256:243 for the lowest interval:
hypate parhypate lichanos mese 4:3 9:7 9:8 1:1 | 28:27 | 8:7 | 9:8 | -498 -435 -204 0 cents
Didymus described the following tuning, similar to Ptolemy's later tense diatonic, but reversing the order of the 10:9 and 9:8, namely:
hypate parhypate lichanos mese 4:3 5:4 9:8 1:1 | 16:15 | 10:9 | 9:8 | -498 -386 -204 0 cents
Ptolemy, following Aristoxenus, also described "tense" and "relaxed" ("intense" and "soft") tunings. His "tense diatonic", as used in Ptolemy's intense diatonic scale, is:
hypate parhypate lichanos mese 4:3 5:4 10:9 1:1 | 16:15 | 9:8 | 10:9 | -498 -386 -182 0 cents
Ptolemy's "relaxed diatonic" ("soft diatonic") was:
hypate parhypate lichanos mese 4:3 80:63 8:7 1:1 | 21:20 | 10:9 | 8:7 | -498 -413 -231 0 cents
Ptolemy described his "equable" or "even diatonic" as sounding foreign or rustic, and its neutral seconds are reminiscent of scales used in Arabic music.[citation needed] It is based on an equal division of string lengths (thus presumably simple to build and "rustic"), which implies a harmonic series of pitch frequencies:
hypate parhypate lichanos mese 4:3 11:9 10:9 1:1 | 12:11 | 11:10 | 10:9 | -498 -347 -182 0 cents
Byzantine music
In Byzantine music most of the modes of the octoechos are based on the diatonic genus, apart from the second mode (both authentic and plagal) which is based on the chromatic genus. Byzantine music theory distinguishes between two tunings of the diatonic genus, the so-called "hard diatonic" on which the third mode and two of the grave modes are based, and the "soft diatonic" on which the first mode (both authentic and plagal) and the fourth mode (both authentic and plagal) are based. The hard tuning of the diatonic genus in Byzantine music may also be referred to as the enharmonic genus; an unfortunate name that persisted, since it can be confused with the ancient enharmonic genus.
Chromatic
Aristoxenus describes the chromatic genus (Greek: χρωματικὸν γένος or χρωματική) as a more recent development than the diatonic.[6] It is characterized by an upper interval of a minor third. The pyknon (πυκνόν), consisting of the two movable members of the tetrachord, is divided into two adjacent semitones.
The scale generated by the chromatic genus is not like the modern twelve-tone chromatic scale. The modern (18th-century) well-tempered chromatic scale has twelve pitches to the octave, and consists of semitones of various sizes; the equal temperament common today, on the other hand, also has twelve pitches to the octave, but the semitones are all of the same size. In contrast, the ancient Greek chromatic scale had seven pitches (i.e. heptatonic) to the octave (assuming alternating conjunct and disjunct tetrachords), and had incomposite minor thirds as well as semitones and whole tones.
The (Dorian) scale generated from the chromatic genus is composed of two chromatic tetrachords:

- E−F−G♭−A || B−C−D♭−E
whereas in modern music theory, a "chromatic scale" is:
- E−F−G♭−G−A♭−A−B♭−B−C−D♭−D−E♭−E
Shades
The number and nature of the shades of the chromatic genus vary amongst the Greek theorists. The major division is between the Aristoxenians and the Pythagoreans. Aristoxenus and Cleonides agree there are three, called soft, hemiolic, and tonic. Ptolemy, representing a Pythagorean view, held that there are five.[13]
Tunings
Theon of Smyrna gives an incomplete account of Thrasyllus of Mendes' formulation of the greater perfect system, from which the diatonic and enharmonic genera can be deduced.
For the chromatic genus, however, all that is given is a 32:27 proportion of mese to lichanos. This leaves 9:8 for the pyknon, but there is no information at all about the position of the chromatic parhypate and therefore of the division of the pyknon into two semitones, though it may have been the limma of 256:243, as Boethius does later.[14] Someone has referred to this speculative reconstructions as the traditional Pythagorean tuning of the chromatic genus[citation needed]:
hypate parhypate lichanos mese 4:3 81:64 32:27 1:1 | 256:243 | 2187:2048 | 32:27 | -498 -408 -294 0 cents
Archytas used the simpler and more consonant 9:7, which he used in all three of his genera. His chromatic division is:[15]
hypate parhypate lichanos mese 4:3 9:7 32:27 1:1 | 28:27 | 243:224 | 32:27 | -498 -435 -294 0 cents
According to Ptolemy's calculations, Didymus's chromatic has only 5-limit intervals, with the smallest possible numerators and denominators.[16] The successive intervals are all superparticular ratios:
hypate parhypate lichanos mese 4:3 5:4 6:5 1:1 | 16:15 | 25:24 | 6:5 | -498 -386 -316 0 cents
Byzantine music
In Byzantine music the chromatic genus is the genus on which the second mode and second plagal mode are based. The "extra" mode nenano is also based on this genus.[citation needed]
Enharmonic
Aristoxenus describes the enharmonic genus (Ancient Greek: [γένος] ἐναρμόνιον; Latin: enarmonium, [genus] enarmonicum, harmonia) as the "highest and most difficult for the senses".[6] Historically it has been the most mysterious and controversial of the three genera. Its characteristic interval is a ditone (or major third in modern terminology), leaving the pyknon to be divided by two intervals smaller than a semitone called dieses (approximately quarter tones, though they could be calculated in a variety of ways). Because it is not easily represented by Pythagorean tuning or meantone temperament, there was much fascination with it in the Renaissance.
In the modern tuning system of twelve-tone equal temperament, enharmonic refers to tones that are identical, but spelled differently. In other tuning systems, enharmonic notes, such as C♯ and D♭, may be close but not identical, differing by a comma (an interval smaller than a semitone, like a diesis).
Notation
Modern notation for enharmonic notes requires two special symbols for raised and lowered quarter tones or half-semitones or quarter steps. Some symbols used for a quarter-tone flat are a downward-pointing arrow ↓, or a flat combined with an upward-pointing arrow ↑. Similarly, for a quarter-tone sharp, an upward-pointing arrow may be used, or else a sharp with a downward-pointing arrow. Three-quarter flat and sharp symbols are formed similarly.[17] A further modern notation involves reversed flat signs for quarter-flat, so that an enharmonic tetrachord may be represented:
- D E
 F
F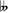 G ,
G ,
or
- A B
 C
C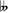 D .
D .
The double-flat symbol (![]() ) is used for modern notation of the third tone in the tetrachord to follow modern convention of keeping scale notes as a letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F
) is used for modern notation of the third tone in the tetrachord to follow modern convention of keeping scale notes as a letter sequence, and to remind the reader that the third tone in an enharmonic tetrachord (say F![]() , shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the expected E♭ instead of F
, shown above) was not tuned quite the same as the second note in a diatonic or chromatic scale (the expected E♭ instead of F![]() ).
).
Scale
Like the diatonic scale, the ancient Greek enharmonic scale also had seven notes to the octave (assuming alternating conjunct and disjunct tetrachords), not 24 as one might imagine by analogy to the modern chromatic scale.[18][page needed] A scale generated from two disjunct enharmonic tetrachords is:
- D E
 F
F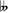 G ‖ A B
G ‖ A B C
C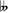 D
D
or, in music notation starting on E: ![]() ,
with the corresponding conjunct tetrachords forming
,
with the corresponding conjunct tetrachords forming
- A B
 C
C | D | E
| D | E F
F G
G
or, transposed to E like the previous example:  .
.
Tunings
The precise ancient Pythagorean tuning of the enharmonic genus is not known.[19] Aristoxenus believed that the pyknon evolved from an originally pentatonic trichord in which a perfect fourth was divided by a single "infix"—an additional note dividing the fourth into a semitone plus a major third (e.g., E, F, A, where F is the infix dividing the fourth E–A). Such a division of a fourth necessarily produces a scale of the type called pentatonic, because compounding two such segments into an octave produces a scale with just five steps. This became an enharmonic tetrachord by the division of the semitone into two quarter tones (E, E↑, F, A).[20]
Archytas[21][22] used 9:7 in all three of his genera;[19] here it is the mediant of 4:3 and 5:4, as (4+5):(3+4) = 9:7:
hypate parhypate lichanos mese 4:3 9:7 5:4 1:1 | 28:27 |36:35| 5:4 | -498 -435 -386 0 cents
Didymus uses the same major third (5:4) but divides the pyknon with the arithmetic mean of the string lengths[21] (if one wishes to think in terms of frequencies, rather than string lengths or interval distance down from the tonic, as the example below does, splitting the interval between the frequencies 4:3 and 5:4 by their harmonic mean 31:24 will result in the same sequence of intervals as below):[19][failed verification]
hypate parhypate lichanos mese 4:3 31:24 5:4 1:1 |32:31 |31:30 | 5:4 | -498 -443 -386 0 cents
This method splits the 16:15 half-step pyknon into two nearly equal intervals, the difference in size between 31:30 and 32:31 being less than 2 cents.