A quarter tone is a pitch halfway between the usual notes of a chromatic scale or an interval about half as wide (orally, or logarithmically) as a semitone, which itself is half a whole tone. Quarter tones divide the octave by 50 cents each, and have 24 different pitches.

Quarter tones have their roots in the music of the Middle East and more specifically in Persian traditional music.[1] However, the first evidenced proposal of the equally-tempered quarter tone scale, or 24 equal temperament, was made by 19th-century music theorists Heinrich Richter in 1823[2] and Mikhail Mishaqa about 1840.[3] Composers who have written music using this scale include: Pierre Boulez, Julián Carrillo, Mildred Couper, George Enescu, Alberto Ginastera, Gérard Grisey, Alois Hába, Ljubica Marić, Charles Ives, Tristan Murail, Krzysztof Penderecki, Giacinto Scelsi, Ammar El Sherei, Karlheinz Stockhausen, Tui St. George Tucker, Ivan Wyschnegradsky, Iannis Xenakis, and Seppe Gebruers (See List of quarter tone pieces.)
Types
[edit]Equal-tempered tuning systems
[edit]
 –G–A
–G–A ) as good possibility for a "fundamental" chord in the quarter-tone scale, akin not to the tonic but to the major chord of traditional tonality.[4]
) as good possibility for a "fundamental" chord in the quarter-tone scale, akin not to the tonic but to the major chord of traditional tonality.[4]
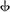 =A
=A , 19 quarter tones. It approximates the harmonic seventh, B
, 19 quarter tones. It approximates the harmonic seventh, B ♭. Maneri-Sims notation: B
♭. Maneri-Sims notation: B ♭
♭The term quarter tone can refer to a number of different intervals, all very close in size. For example, some 17th- and 18th-century theorists used the term to describe the distance between a sharp and enharmonically distinct flat in mean-tone temperaments (e.g., D♯–E♭).[2] In the quarter-tone scale, also called 24-tone equal temperament (24-TET), the quarter tone is 50 cents, or a frequency ratio of 24√2 or approximately 1.0293, and divides the octave into 24 equal steps (equal temperament). In this scale the quarter tone is the smallest step. A semitone is thus made of two steps, and three steps make a three-quarter tone or neutral second, half of a minor third. The 8-TET scale is composed of three-quarter tones. Four steps make a whole tone.
Quarter tones and intervals close to them also occur in a number of other equally tempered tuning systems. 22-TET contains an interval of 54.55 cents, slightly wider than a quarter-tone, whereas 53-TET has an interval of 45.28 cents, slightly smaller. 72-TET also has equally tempered quarter-tones, and indeed contains three quarter-tone scales, since 72 is divisible by 24. The smallest interval in 31 equal temperament (the "diesis" of 38.71 cents) is half a chromatic semitone, one-third of a diatonic semitone and one-fifth of a whole tone, so it may function as a quarter tone, a fifth-tone or a sixth-tone.
Just intonation tuning systems
[edit]In just intonation the quarter tone can be represented by the septimal quarter tone, 36:35 (48.77 cents), or by the undecimal quarter tone (i.e. the thirty-third harmonic), 33:32 (53.27 cents), approximately half the semitone of 16:15 or 25:24. The ratio of 36:35 is only 1.23 cents narrower than a 24-TET quarter tone. This just ratio is also the difference between a minor third (6:5) and septimal minor third (7:6).
Composer Ben Johnston, to accommodate the just septimal quarter tone, uses a small "7" (![]() ) as an accidental to indicate a note is lowered 49 cents, or an upside down "7" (
) as an accidental to indicate a note is lowered 49 cents, or an upside down "7" (![]() ) to indicate a note is raised 49 cents,[5] or a ratio of 36:35.[6] Johnston uses an upward and downward arrow to indicate a note is raised or lowered by a ratio of 33:32, or 53 cents.[6] The Maneri-Sims notation system designed for 72-et uses the accidentals
) to indicate a note is raised 49 cents,[5] or a ratio of 36:35.[6] Johnston uses an upward and downward arrow to indicate a note is raised or lowered by a ratio of 33:32, or 53 cents.[6] The Maneri-Sims notation system designed for 72-et uses the accidentals ![]() and
and ![]() for a quarter tone (36:35 or 48.77 cents) up and down.
for a quarter tone (36:35 or 48.77 cents) up and down.
Playing quarter tones
[edit]
Any tunable musical instrument can be used to perform quarter tones, if two players and two identical instruments, with one tuned a quarter tone higher, are used. As this requires neither a special instrument nor special techniques, much quarter toned music is written for pairs of pianos, violins, harps, etc. The retuning of the instrument, and then returning it to its former pitch, is easy for violins, harder for harps, and slow and relatively expensive for pianos.
The following deals with the ability of single instruments to produce quarter tones. In Western instruments, this means "in addition to the usual 12-tone system". Because many musical instruments manufactured today (2018) are designed for the 12-tone scale, not all are usable for playing quarter tones. Sometimes special playing techniques must be used.
Conventional musical instruments that cannot play quarter tones (except by using special techniques—see below) include:
- Most standard or unmodified non-electronic keyboard instruments, such as pianos, organs, and accordions
- Fretted string instruments such as guitars, bass guitars, and ukuleles (though on these it is possible to play quarter tones by pitch-bending, with special tunings, or with customized necks)
- Pitched percussion instruments, if standard techniques are used, and if the instruments are not tunable
- Western wind instruments that use keys or valves
- Woodwind instruments, such as clarinets, saxophones, flutes, and oboes (though with many of these, it is still possible using non-standard techniques such as special fingerings or by the player manipulating their embouchure, to play at least some quarter tones, if not a whole scale)
- Valved brass instruments (trumpet, tuba) (though, as with woodwinds, embouchure manipulation, as well as harmonic tones that fall closer to quarter-tones than half-tones, make quarter-tone scales possible; the horn technique of adjusting pitch with the right hand in the bell makes this instrument an exception)
- Harmonica (although note bending is a common technique)
Conventional musical instruments that can play quarter tones include
- Electronic instruments:
- Synthesizers, using either special keyboard controllers or continuous-pitch controllers such as fingerboard controllers, or when controlled by a sequencer capable of outputting quarter-tone control signals.
- Theremins and other continuously pitched instruments
- Fretless string instruments, such as the violin family, fretless guitars, fretless electric basses, ouds, and members of the huqin family of instruments.
- String instruments with movable frets (such as the sitar)
- Specially fretted string instruments (such as the Turkish bağlama).
- Fretted string instruments specially tuned to quarter tones
- Pedal steel guitar
- Wind instruments whose main means of tone-control is a slide, such as trombones, the tromboon invented by P. D. Q. Bach, the slide trumpet and the slide whistle
- Specially keyed woodwind instruments. A quarter tone clarinet was built by Fritz Schüller (1883–1977) of Markneukirchen, and a quarter tone mechanism for flutes by Eva Kingma.[7]
- Valved brass instruments with extra, quarter-tone valves, and natural brass instruments that play through the 11th and 13th partials of the harmonic series
- Voice
- Kazoo
- Pitched percussion instruments, when tuning permits (e.g., timpani), or using special techniques
Other instruments can be used to play quarter tones when using audio signal processing effects such as pitch shifting.
Quarter-tone pianos have been built, which consist essentially of two pianos with two keyboards stacked one above the other in a single case, one tuned a quarter tone higher than the other.[citation needed]
Music of the Middle East
[edit]Many Persian dastgah and Arabic maqamat contain intervals of three-quarter tone size; a short list of these follows.[8]
- Bayati (بیاتی): D E
 F G A B♭ C D
F G A B♭ C D
- Rast (راست):
- Saba (صبا): D E
 F G♭ A B♭ C D
F G♭ A B♭ C D
- Sigah (سه گاه): E
 F G A B
F G A B C D E
C D E
- ‘Ajam (عجم)
- Hoseyni
The Islamic philosopher and scientist Al-Farabi described a number of intervals in his work in music, including a number of quarter tones.
Assyrian/Syriac Church Music Scale:[9]
- Qadmoyo (Bayati)
- Trayono (Hussayni)
- Tlithoyo (Segah)
- Rbiʿoyo (Rast)
- Hmishoyo
- Shtithoyo (ʿAjam)
- Shbiʿoyo
- Tminoyo
Quarter-tone scale
[edit]Known as gadwal in Arabic,[8] the quarter-tone scale was developed in the Middle East in the eighteenth century and many of the first detailed writings in the nineteenth century Syria describe the scale as being of 24 equal tones.[10] The invention of the scale is attributed to Mishaqa who wrote a book devoted to the topic[11] but made clear that his teacher, Sheikh Muhammad al-Attar (1764–1828), was one among many already familiar with the concept.[12]

The quarter tone scale may be primarily a theoretical construct in Arabic music. The quarter tone gives musicians a "conceptual map" they can use to discuss and compare intervals by number of quarter tones, and this may be one of the reasons it accompanies a renewed interest in theory, with instruction in music theory a mainstream requirement since that period.[10]
Previously, pitches of a mode were chosen from a scale consisting of seventeen tones, developed by Safi al-Din al-Urmawi in the thirteenth century.[12]

Composer Charles Ives chose the chord C–D![]() –F–G
–F–G![]() –B♭ as good possibility for a "secondary" chord in the quarter-tone scale, akin to the minor chord of traditional tonality. He considered that it may be built upon any degree of the quarter tone scale[4] Here is the secondary "minor" and its "first inversion":
–B♭ as good possibility for a "secondary" chord in the quarter-tone scale, akin to the minor chord of traditional tonality. He considered that it may be built upon any degree of the quarter tone scale[4] Here is the secondary "minor" and its "first inversion":
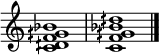
In popular Western music
[edit]
The bass descent of Nancy Sinatra's version of "These Boots Are Made for Walkin'" includes quarter tone descents.[13] Several quarter-tone albums have been recorded by Jute Gyte, a one-man avantgarde black metal band from Missouri, USA.[14][15] Another quartertone metal album was issued by the Swedish band Massive Audio Nerve.[16] Australian psychedelic rock band King Gizzard & the Lizard Wizard's albums Flying Microtonal Banana, K.G., and L.W. heavily emphasize quarter-tones and used a custom-built guitar in 24 TET tuning.[17] Jazz violinist / violist Mat Maneri, in conjunction with his father Joe Maneri, made a crossover fusion album, Pentagon (2005),[18] that featured experiments in hip hop with quarter tone pianos, as well as electric organ and mellotron textures, along with distorted trombone, in a post-Bitches Brew type of mixed jazz / rock.[19]
Later, Seppe Gebruers started playing and improvising with two pianos tuned a quarter-tone apart. In 2019 he started a research project at the Royal Conservatory of Ghent, titled 'Unexplored possibilities of contemporary improvisation and the influence of microtonality in the creation process'.[20] With two pianos tuned a quarter tone apart Gebruers recorded 'The Room: Time & Space' (2018) in a trio formation with drummer Paul Lovens and bassist Hugo Anthunes. In his solo project 'Playing with standards' (album release January 2023), Gebruers plays with famous songs including jazz standards. With Paul Lytton and Nils Vermeulen he forms a 'Playing with standards' trio.
Ancient Greek tetrachords
[edit]The enharmonic genus of the Greek tetrachord consisted of a ditone or an approximate major third, and a semitone, which was divided into two microtones. Aristoxenos, Didymos and others presented the semitone as being divided into two approximate quarter tone intervals of about the same size, while other ancient Greek theorists described the microtones resulting from dividing the semitone of the enharmonic genus as unequal in size (i.e., one smaller than a quarter tone and one larger).[21][22]

Interval size in equal temperament
[edit]Here are the sizes of some common intervals in a 24-note equally tempered scale, with the interval names proposed by Alois Hába (neutral third, etc.) and Ivan Wyschnegradsky (major fourth, etc.):
Interval name Size
(steps)Size
(cents)MIDI Just ratio Just
(cents)MIDI Error
(cents)octave 24 1200 2:1 1200.00 0.00 semidiminished octave 23 1150 35:18 1151.23 −1.23 supermajor seventh 23 1150 27:14 1137.04 +12.96 major seventh 22 1100 15:8 1088.27 +11.73 neutral seventh, major tone 21 1050 11:6 1049.36 +0.64 neutral seventh, minor tone 21 1050 20:11 1035.00 +15.00 large just minor seventh 20 1000 9:5 1017.60 −17.60 small just minor seventh 20 1000 16:9 996.09 +3.91 supermajor sixth/subminor seventh 19 950 7:4 968.83 −18.83 major sixth 18 900 5:3 884.36 +15.64 neutral sixth 17 850 18:11 852.59 −2.59 minor sixth 16 800 8:5 813.69 −13.69 subminor sixth 15 750 14:9 764.92 −14.92 perfect fifth 14 700 3:2 701.96 −1.96 minor fifth 13 650 16:11 648.68 +1.32 lesser septimal tritone 12 600 7:5 582.51 +17.49 major fourth 11 550 11:8 551.32 −1.32 perfect fourth 10 500 4:3 498.04 +1.96 tridecimal major third 9 450 13:10 454.21 −4.21 septimal major third 9 450 9:7 435.08 +14.92 major third 8 400 5:4 386.31 +13.69 undecimal neutral third 7 350 11:9 347.41 +2.59 minor third 6 300 6:5 315.64 −15.64 septimal minor third 5 250 7:6 266.87 −16.87 tridecimal five-quarter tone 5 250 15:13 247.74 +2.26 septimal whole tone 5 250 8:7 231.17 +18.83 major second, major tone 4 200 9:8 203.91 −3.91 major second, minor tone 4 200 10:9 182.40 +17.60 neutral second, greater undecimal 3 150 11:10 165.00 −15.00 neutral second, lesser undecimal 3 150 12:11 150.64 −0.64 15:14 semitone 2 100 15:14 119.44 −19.44 diatonic semitone, just 2 100 16:15 111.73 −11.73 21:20 semitone 2 100 21:20 84.47 +15.53 28:27 semitone 1 50 28:27 62.96 −12.96 33:32 semitone 1 50 33:32 53.27 −3.27 unison 0 0 1:1 0.00 0.00
Moving from 12-TET to 24-TET allows the better approximation of a number of intervals. Intervals matched particularly closely include the neutral second, neutral third, and (11:8) ratio, or the 11th harmonic. The septimal minor third and septimal major third are approximated rather poorly; the (13:10) and (15:13) ratios, involving the 13th harmonic, are matched very closely. Overall, 24-TET can be viewed as matching the 11th and 13th harmonics more closely than the 7th.
See also
[edit]References
[edit]- ^ Hormoz Farhat (2004). The Dastgah Concept in Persian Music. Cambridge University Press. ISBN 0-521-54206-5
- ^ a b Julian Rushton, "Quarter-Tone", The New Grove Dictionary of Music and Musicians, second edition, edited by Stanley Sadie and John Tyrrell (London: Macmillan, 2001).
- ^ Touma, Habib Hassan (1996). The Music of the Arabs, p. 16. Translator: Laurie Schwartz. Portland, Oregon: Amadeus Press. ISBN 0-931340-88-8.
- ^ a b Boatwright, Howard (1965). "Ives' Quarter-Tone Impressions", Perspectives of New Music 3, no. 2 (Spring–Summer): pp. 22–31; citations on pp. 27–28; reprinted in Perspectives on American Composers, edited by Benjamin Boretz and Edward T. Cone, pp. 3–12, New York: W. W. Norton, 1971, citation on pp. 8–9. "These two chords outlined above might be termed major and minor."
- ^ Douglas Keislar; Easley Blackwood; John Eaton; Lou Harrison; Ben Johnston; Joel Mandelbaum; William Schottstaedt. p.193. "Six American Composers on Nonstandard Tunnings", Perspectives of New Music, vol. 29, no. 1. (Winter 1991), pp. 176–211.
- ^ a b Fonville, John (Summer, 1991). "Ben Johnston's Extended Just Intonation: A Guide for Interpreters", p. 114, Perspectives of New Music, vol. 29, no. 2, pp. 106–137.
- ^ Kingma System
- ^ a b Spector, Johanna (May 1970). "Classical ʿUd Music in Egypt with Special Reference to Maqamat". Ethnomusicology. 14 (2): 243–257. doi:10.2307/849799. JSTOR 849799.
- ^ Asaad, Gabriel (1990). Syria's Music Throughout History
- ^ a b Marcus, Scott (Spring–Summer 1993). "The interface between theory and practice: Intonation in Arab music". Asian Music. 24 (2): 39–58. doi:10.2307/834466. JSTOR 834466.
- ^ Mishaqa, Mikhiiʾil (c. 1840). al-Risāla al-shihābiyya fi 'l-ṣināʿa al-mūsīqiyya [Essay on the Art of Music for the Emir Shihāb] (in Arabic).
- ^ a b Maalouf, Shireen (October–December 2003). "Mikhiiʾil Mishiiqa: Virtual founder of the twenty-four equal quartertone scale". Journal of the American Oriental Society. 123 (4): 835–840. doi:10.2307/3589971. JSTOR 3589971.
- ^ Everett, Walter (2009). The Foundations of Rock. Oxford University Press. p. 32. ISBN 9780195310238.
- ^ Tremblay, Dæv (3 September 2014). "Jute Gyte – Ressentiment". canthisbecalledmusic.com (album review).
- ^ Gyte, Jute. Discontinuities. jutegyte.bandcamp.com (music album). (commerical site).
- ^ "Massive Audio Nerve's album Cancer Vulgaris in July". blabbermouth.net.
- ^ Huguenor, Mike (21 August 2017). "King Gizzard & the Lizard Wizard talk new album Flying Microtonal Banana". Guitar World (guitarworld.com) (interview). Retrieved 2021-01-27.
- ^ Maneri, M.; Maneri, J. (2005). Pentagon (music album).
- ^ Maneri, Mat (1 December 2005). "Pentagon by Will Layman". PopMatters (album review).
- ^ "Seppe Gebruers - Playing with Standards".
- ^
Chalmers, John H., Jr. (1993). Divisions of the Tetrachord. Hanover, NH: Frog Peak Music. Chapter 5, page 49. ISBN 0-945996-04-7.
((cite book)): CS1 maint: multiple names: authors list (link) - ^ West, Martin L. (1992). Ancient Greek Music. Oxford, UK: Oxford University Press. ISBN 0-19-814975-1.
Further reading
[edit]- Bartolozzi, Bruno (1967). New Sounds for Woodwind. London, UK / New York, NY: Oxford University Press.
- Bousted, Donald (Fall 2002). "Microtonality, the recorder and the quarter-tone recorder manual". The Recorder Magazine. Vol. 22, no. 3. pp. 99–102.
- Bousted, Donald (Fall 2005). "Next step quarter-tone resources: Melody". The Recorder Magazine. Vol. 25, no. 3. pp. 88–91.
- Caravan, Ronald R. (1979). Preliminary Exercises and Etudes in Contemporary Techniques for Clarinet: Introductory material for the study of multiphonics, quarter tones, and timbre variation. Oswego, NY: Ethos Publications.
- Ellis, Don (1975). Quarter Tones: A text with musical examples, exercises, and etudes. Plainview, NY: Harold Branch.
- MacDonald, John (1822). A Treatise on the Harmonic System Arising from the Vibrations of the Aliquot Divisions of Strings. London, UK: T. Preston.
- Möllendorff, Willi; Monzo, Joe (2001). Music with Quarter-Tones: Experiences at the bichromatic harmonium. U.S.: J. Monzo.
- Rees, Carla (2007). "Eva Kingma and the quarter-tone flute". Pan: The Flute Magazine. 26 (4): 23–29.
- Rewoldt, Todd (2000). "Altissimo quarter-tones for the alto saxophone". Saxophone Symposium. 25: 56–69.
External links
[edit]- "quarter-tone / 24-edo", TonalSoft.com
| Twelve- semitone (post-Bach Western) |
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Other tuning systems |
| ||||||||||||||
| Other intervals |
| ||||||||||||||
| Composers |
| ||||||
|---|---|---|---|---|---|---|---|
| Inventors | |||||||
| Tunings and scales |
| ||||||
| Concepts and techniques | |||||||
| Groups and publications | |||||||
| Compositions | |||||||
| Other topics | |||||||
| Measurement | |||||||
|---|---|---|---|---|---|---|---|
| Just intonation | |||||||
| Temperaments |
| ||||||
| Traditional non-Western | |||||||
| Non-octave |
| ||||||




