
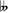 vs. C♯.
vs. C♯.In music theory and tuning, the kleisma (κλείσμα), or semicomma majeur,[1] is a minute and barely perceptible comma type interval important to musical temperaments. It is the difference between six justly tuned minor thirds (each with a frequency ratio of 6/5) and one justly tuned tritave or perfect twelfth (with a frequency ratio of 3/1, formed by a 2/1 octave plus a 3/2 perfect fifth). It is equal to a frequency ratio of 15625/15552 = 2−6 3−5 56, or approximately 8.1 cents (). It can be also defined as the difference between five justly tuned minor thirds and one justly tuned major tenth (of size 5/2, formed by a 2/1 octave plus a 5/4 major third) or as the difference between a chromatic semitone (25/24) and a greater diesis (648/625).
The interval was named by Shohé Tanaka after the Greek for "closure",[2] who noted that it was tempered out to a unison by 53 equal temperament.[3] It is also tempered out in 19, 34, and 72 equal temperament.
12 and 24 equal temperament, however, inflate the kleisma up to an entire semitone instead of tempering it out, as six minor thirds are equal to 18 semitones, while a perfect twelfth is 19 semitones. The same is true for the difference between five minor thirds (15 semitones) and one major tenth (16 semitones).
The interval was described but not used by Rameau in 1726.[2]
Larry Hanson[4] independently discovered this interval which also manifested in a unique mapping using a generalized keyboard capable of accommodating all the above temperaments as well as just intonation constant structures (periodicity blocks) with these numbers of scale degrees
The kleisma is also an interval important to the Bohlen–Pierce scale.
References
[edit]- ^ Haluska, Jan (2003). The Mathematical Theory of Tone Systems, p.xxviii. ISBN 978-0-8247-4714-5.
- ^ a b Just Intonation Network (1993). 1/1: The Quarterly Journal of the Just Intonation Network, Volume 8, p.19.
- ^ Studien im Gebiete der reinen Stimmung, in: Vierteljahrsschrift für Musikwissenschaft, Band 6, Nr. 1, Breitkopf und Härtel, Leipzig 1890, pp. 1-90 (Goole-Scan)
- ^ Hanson, Larry (1989). "Development of a 53-Tone Keyboard Layout", Xenharmonikon XII.
| Twelve- semitone (post-Bach Western) |
| ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Other tuning systems |
| ||||||||||||||
| Other intervals |
| ||||||||||||||