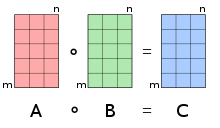
In mathematics, the Hadamard product (also known as the element-wise product, entrywise product^{[1]: ch. 5} or Schur product^[2]) is a binary operation that takes in two matrices of the same dimensions and returns a matrix of the multiplied corresponding elements. This operation can be thought as a "naive matrix multiplication" and is different from the matrix product. It is attributed to, and named after, either French-Jewish mathematician Jacques Hadamard or German-Jewish mathematician Issai Schur.

The Hadamard product is associative and distributive. Unlike the matrix product, it is also commutative.^[3]

Definition

For two matrices A and B of the same dimension m × n, the Hadamard product ${\displaystyle A\circ B}$ (or ${\displaystyle A\odot B}$^[4][5][6]) is a matrix of the same dimension as the operands, with elements given by^[3]

${\displaystyle (A\circ B)_{ij}=(A\odot B)_{ij}=(A)_{ij}(B)_{ij}.}$

For matrices of different dimensions (m × n and p × q, where m ≠ p or n ≠ q), the Hadamard product is undefined.

For example, the Hadamard product for two arbitrary 2 × 3 matrices is:

${\displaystyle {\begin{bmatrix}2&3&1\\0&8&-2\end{bmatrix))\circ {\begin{bmatrix}3&1&4\\7&9&5\end{bmatrix))={\begin{bmatrix}2\times 3&3\times 1&1\times 4\\0\times 7&8\times 9&-2\times 5\end{bmatrix))={\begin{bmatrix}6&3&4\\0&72&-10\end{bmatrix))}$

Properties

• The Hadamard product is commutative (when working with a commutative ring), associative and distributive over addition. That is, if A, B, and C are matrices of the same size, and k is a scalar:
  $${\displaystyle {\begin{aligned}A\circ B&=B\circ A,\\A\circ (B\circ C)&=(A\circ B)\circ C,\\A\circ (B+C)&=A\circ B+A\circ C,\\\left(kA\right)\circ B&=A\circ \left(kB\right)=k\left(A\circ B\right),\\A\circ 0&=0\circ A=0.\end{aligned))}$$

  
• The identity matrix under Hadamard multiplication of two m × n matrices is an m × n matrix where all elements are equal to 1. This is different from the identity matrix under regular matrix multiplication, where only the elements of the main diagonal are equal to 1. Furthermore, a matrix has an inverse under Hadamard multiplication if and only if none of the elements are equal to zero.^[7]
• For vectors x and y, and corresponding diagonal matrices D_x and D_y with these vectors as their main diagonals, the following identity holds:^[1]: 479
  $${\displaystyle \mathbf {x} ^{*}(A\circ B)\mathbf {y} =\operatorname {tr} \left({D}_{\mathbf {x} }^{*}A{D}_{\mathbf {y} }{B}^{\mathsf {T))\right),}$$

  
  where x^* denotes the conjugate transpose of x. In particular, using vectors of ones, this shows that the sum of all elements in the Hadamard product is the trace of AB^T where superscript T denotes the matrix transpose, that is, ${\displaystyle \operatorname {tr} \left(AB^{\mathsf {T))\right)=\mathbf {1} ^{\mathsf {T))\left(A\circ B\right)\mathbf {1} }$. A related result for square A and B, is that the row-sums of their Hadamard product are the diagonal elements of AB^T:^[8]
  $${\displaystyle \sum _{i}(A\circ B)_{ij}=\left(B^{\mathsf {T))A\right)_{jj}=\left(AB^{\mathsf {T))\right)_{ii}.}$$

  
  Similarly,
  $${\displaystyle \left(\mathbf {y} \mathbf {x} ^{*}\right)\circ A={D}_{\mathbf {y} }A{D}_{\mathbf {x} }^{*))$$

  
  Furthermore, a Hadamard matrix-vector product can be expressed as:
  $${\displaystyle (A\circ B)\mathbf {y} =\operatorname {diag} \left(AD_{\mathbf {y} }B^{\mathsf {T))\right)}$$

  
  where ${\displaystyle \operatorname {diag} (M)}$ is the vector formed from the diagonals of matrix M.
• The Hadamard product is a principal submatrix of the Kronecker product.^[9][10]
• The Hadamard product satisfies the rank inequality
  $${\displaystyle \operatorname {rank} (A\circ B)\leq \operatorname {rank} (A)\operatorname {rank} (B)}$$

  
• If A and B are positive-definite matrices, then the following inequality involving the Hadamard product holds:^[11]
  $${\displaystyle \prod _{i=k}^{n}\lambda _{i}(A\circ B)\geq \prod _{i=k}^{n}\lambda _{i}(AB),\quad k=1,\ldots ,n,}$$

  
  where λ_i(A) is the ith largest eigenvalue of A.
• If D and E are diagonal matrices, then^[12]
  $${\displaystyle {\begin{aligned}D(A\circ B)E&=(DAE)\circ B=(DA)\circ (BE)\\&=(AE)\circ (DB)=A\circ (DBE).\end{aligned))}$$

  
• The Hadamard product of two vectors ${\displaystyle \mathbf {a} }$ and ${\displaystyle \mathbf {b} }$ is the same as matrix multiplication of one vector by the corresponding diagonal matrix of the other vector:
  $${\displaystyle \mathbf {a} \circ \mathbf {b} =D_{\mathbf {a} }\mathbf {b} =D_{\mathbf {b} }\mathbf {a} }$$

  
• The vector to diagonal matrix ${\displaystyle \operatorname {diag} }$ operator may be expressed using the Hadamard product as:
  $${\displaystyle \operatorname {diag} (\mathbf {a} )=(\mathbf {a} \mathbf {1} ^{T})\circ I}$$

  
  where ${\displaystyle \mathbf {1} }$ is a constant vector with elements ${\displaystyle 1}$ and ${\displaystyle I}$ is the identity matrix.

The mixed-product property

$${\displaystyle (A\otimes B)\circ (C\otimes D)=(A\circ C)\otimes (B\circ D),}$$

${\displaystyle \otimes }$

${\displaystyle A}$

${\displaystyle C}$

${\displaystyle B}$

${\displaystyle D}$

$${\displaystyle (A\bullet B)\circ (C\bullet D)=(A\circ C)\bullet (B\circ D),}$$

${\displaystyle \bullet }$

$${\displaystyle (A\bullet B)(C\ast D)=(AC)\circ (BD),}$$

${\displaystyle \ast }$

Schur product theorem

The Hadamard product of two positive-semidefinite matrices is positive-semidefinite.^[3][8] This is known as the Schur product theorem,^[7] after Russian mathematician Issai Schur. For two positive-semidefinite matrices A and B, it is also known that the determinant of their Hadamard product is greater than or equal to the product of their respective determinants:^[8]

$${\displaystyle \det({A}\circ {B})\geq \det({A})\det({B}).}$$

In programming languages

Hadamard multiplication is built into certain programming languages under various names. In MATLAB, GNU Octave, GAUSS and HP Prime, it is known as array multiplication, or in Julia broadcast multiplication, with the symbol .*.^[14] In Fortran, R,^[15] APL, J and Wolfram Language (Mathematica), it is done through simple multiplication operator * or ×, whereas the matrix product is done through the function matmul, %*%, +.×, +/ .* and the . operators, respectively. In Python with the NumPy numerical library, multiplication of array objects as a*b produces the Hadamard product, and multiplication as a@b produces the matrix product. With the SymPy symbolic library, multiplication of array objects as both a*b and a@b will produce the matrix product, the Hadamard product can be obtained with a.multiply_elementwise(b).^[16] In C++, the Eigen library provides a cwiseProduct member function for the Matrix class (a.cwiseProduct(b)), while the Armadillo library uses the operator % to make compact expressions (a % b; a * b is a matrix product). R package matrixcalc introduces function hadamard.prod() for Hadamard Product of numeric matrices or vectors.

Applications

The Hadamard product appears in lossy compression algorithms such as JPEG. The decoding step involves an entry-for-entry product, in other words the Hadamard product.^{[citation needed]}

In image processing, the Hadamard operator can be used for enhancing, suppressing or masking image regions. One matrix represents the original image, the other acts as weight or masking matrix.

It is used in the machine learning literature, for example, to describe the architecture of recurrent neural networks as GRUs or LSTMs.^[17]

It is also used to study the statistical properties of random vectors and matrices. ^[18][19]

Analogous operations

Other Hadamard operations are also seen in the mathematical literature,^[20] namely the Hadamard root and Hadamard power (which are in effect the same thing because of fractional indices), defined for a matrix such that:

For

$${\displaystyle {\begin{aligned}{B}&={A}^{\circ 2}\\B_{ij}&={A_{ij))^{2}\end{aligned))}$$

and for

$${\displaystyle {\begin{aligned}{B}&={A}^{\circ {\frac {1}{2))}\\B_{ij}&={A_{ij))^{\frac {1}{2))\end{aligned))}$$

The Hadamard inverse reads:^[20]

$${\displaystyle {\begin{aligned}{B}&={A}^{\circ -1}\\B_{ij}&={A_{ij))^{-1}\end{aligned))}$$

A Hadamard division is defined as:^[21][22]

$${\displaystyle {\begin{aligned}{C}&={A}\oslash {B}\\C_{ij}&={\frac {A_{ij)){B_{ij))}\end{aligned))}$$

The penetrating face product

According to the definition of V. Slyusar the penetrating face product of the p×g matrix ${\displaystyle {A))$ and n-dimensional matrix ${\displaystyle {B))$ (n > 1) with p×g blocks (${\displaystyle {B}=[B_{n}]}$) is a matrix of size ${\displaystyle {B))$ of the form:^[23]

$${\displaystyle {A}[\circ ]{B}=\left[{\begin{array}{c | c | c | c }{A}\circ {B}_{1}&{A}\circ {B}_{2}&\cdots &{A}\circ {B}_{n}\end{array))\right].}$$

Example

If

$${\displaystyle {A}={\begin{bmatrix}1&2&3\\4&5&6\\7&8&9\end{bmatrix)),\quad {B}=\left[{\begin{array}{c | c | c }{B}_{1}&{B}_{2}&{B}_{3}\end{array))\right]=\left[{\begin{array}{c c c | c c c | c c c }1&4&7&2&8&14&3&12&21\\8&20&5&10&25&40&12&30&6\\2&8&3&2&4&2&7&3&9\end{array))\right]}$$

then

$${\displaystyle {A}[\circ ]{B}=\left[{\begin{array}{c c c | c c c | c c c }1&8&21&2&16&42&3&24&63\\32&100&30&40&125&240&48&150&36\\14&64&27&14&32&18&49&24&81\end{array))\right].}$$

Main properties

${\displaystyle {A}[\circ ]{B}={B}[\circ ]{A};}$^[23]

${\displaystyle {M}\bullet {M}={M}[\circ ]\left({M}\otimes \mathbf {1} ^{\textsf {T))\right),}$

where ${\displaystyle \bullet }$ denotes the face-splitting product of matrices,

${\displaystyle \mathbf {c} \bullet {M}=\mathbf {c} [\circ ]{M},}$ where ${\displaystyle \mathbf {c} }$ is a vector.

Applications

The penetrating face product is used in the tensor-matrix theory of digital antenna arrays.^[23] This operation can also be used in artificial neural network models, specifically convolutional layers.^[24]