Rotational frequency
SI unit	Hz
Dimension	${\displaystyle {\mathsf {T))^{-1))$

Part of a series on
Classical mechanics
${\displaystyle {\textbf {F))={\frac {d}{dt))(m{\textbf {v)))}$ Second law of motion
History Timeline Textbooks
Branches Applied Celestial Continuum Dynamics Kinematics Kinetics Statics Statistical
Fundamentals Acceleration Angular momentum Couple D'Alembert's principle Energy kinetic potential Force Frame of reference Inertial frame of reference Impulse Inertia / Moment of inertia Mass Mechanical power Mechanical work Moment Momentum Space Speed Time Torque Velocity Virtual work
Formulations Newton's laws of motion Analytical mechanics Lagrangian mechanics Hamiltonian mechanics Routhian mechanics Hamilton–Jacobi equation Appell's equation of motion Koopman–von Neumann mechanics
Core topics Damping Displacement Equations of motion Euler's laws of motion Fictitious force Friction Harmonic oscillator Inertial / Non-inertial reference frame Mechanics of planar particle motion Motion (linear) Newton's law of universal gravitation Newton's laws of motion Relative velocity Rigid body dynamics Euler's equations Simple harmonic motion Vibration
Rotation Circular motion Rotating reference frame Centripetal force Centrifugal force reactive Coriolis force Pendulum Tangential speed Rotational frequency Angular acceleration / displacement / frequency / velocity
Scientists Kepler Galileo Huygens Newton Horrocks Halley Maupertuis Daniel Bernoulli Johann Bernoulli Euler d'Alembert Clairaut Lagrange Laplace Hamilton Poisson Cauchy Routh Liouville Appell Gibbs Koopman von Neumann
Physics portal  Category
v t e

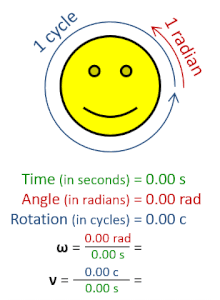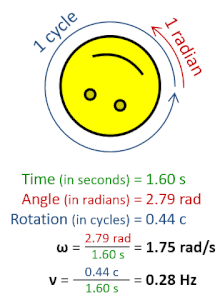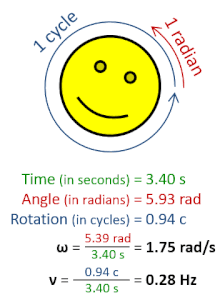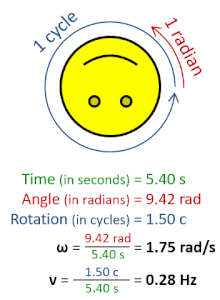
Rotational frequency (also known as rotational speed or rate of rotation) of an object rotating around an axis is the frequency of rotation of the object. Its unit is revolution per minute (rpm), cycle per second (cps), etc.^[1] The symbol for rotational frequency is ${\displaystyle \nu }$ (the Greek lowercase letter nu). Rotational velocity is the vector quantity whose magnitude equals the scalar rotational speed.

Tangential speed ${\displaystyle v}$, rotational frequency ${\displaystyle \nu }$, and radial distance ${\displaystyle r}$, are related by the following equation:^[2]

$${\displaystyle {\begin{aligned}v&=2\pi r\nu \\v&=r\omega .\end{aligned))}$$

An algebraic rearrangement of this equation allows us to solve for rotational frequency:

$${\displaystyle {\begin{aligned}\nu &=v/2\pi r\\\omega &=v/r.\end{aligned))}$$

Thus, the tangential speed will be directly proportional to ${\displaystyle r}$ when all parts of a system simultaneously have the same ${\displaystyle \omega }$, as for a wheel, disk, or rigid wand. The direct proportionality of ${\displaystyle v}$ to ${\displaystyle r}$ is not valid for the planets, because the planets have different rotational frequencies.

Rotational frequency can measure, for example, how fast a motor is running. Rotational speed is sometimes used to mean angular frequency rather than the quantity defined in this article. Angular frequency gives the change in angle per time unit, which is given with the unit radian per second in the SI system. Since 2π radians or 360 degrees correspond to a cycle, we can convert angular frequency to rotational frequency by

$${\displaystyle \nu =\omega /2\pi ,}$$

• ${\displaystyle \nu \,}$ is rotational frequency, with unit cycles per second
• ${\displaystyle \omega \,}$ is angular frequency, with unit radian per second or degree per second

For example, a stepper motor might turn exactly one complete revolution each second. Its angular frequency is 360 degrees per second (360°/s), or 2π radians per second (2π rad/s), while the rotational frequency is 60 rpm.

Rotational frequency is not to be confused with tangential speed, despite some relation between the two concepts. Imagine a merry-go-round with a constant rate of rotation. No matter how close or far you stand from the axis of rotation, your rotational frequency will remain constant. However, your tangential speed does not remain constant. If you stand two meters from the axis of rotation, your tangential speed will be double the amount if you were standing only one meter from the axis of rotation.