| Displacement | |
|---|---|
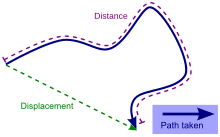 Displacement versus distance travelled along a path | |
Common symbols | d |
| SI unit | metre |
| In SI base units | m |
| Dimension | L |
| Part of a series on |
| Classical mechanics |
|---|
In geometry and mechanics, a displacement is a vector whose length is the shortest distance from the initial to the final position of a point P undergoing motion.[1] It quantifies both the distance and direction of the net or total motion along a straight line from the initial position to the final position of the point trajectory. A displacement may be identified with the translation that maps the initial position to the final position. Displacement is the shift in location when an object in motion changes from one position to another.[2]
A displacement may also be described as a relative position (resulting from the motion), that is, as the final position xf of a point relative to its initial position xi. The corresponding displacement vector can be defined as the difference between the final and initial positions:
In considering motions of objects over time, the instantaneous velocity of the object is the rate of change of the displacement as a function of time. The instantaneous speed, then, is distinct from velocity, or the time rate of change of the distance travelled along a specific path. The velocity may be equivalently defined as the time rate of change of the position vector. If one considers a moving initial position, or equivalently a moving origin (e.g. an initial position or origin which is fixed to a train wagon, which in turn moves on its rail track), the velocity of P (e.g. a point representing the position of a passenger walking on the train) may be referred to as a relative velocity; this is opposed to an absolute velocity, which is computed with respect to a point and coordinate axes which are considered to be at rest (a inertial frame of reference such as, for instance, a point fixed on the floor of the train station and the usual vertical and horizontal directions).
For motion over a given interval of time, the displacement divided by the length of the time interval defines the average velocity, which is a vector, and differs thus from the average speed, which is a scalar quantity.







