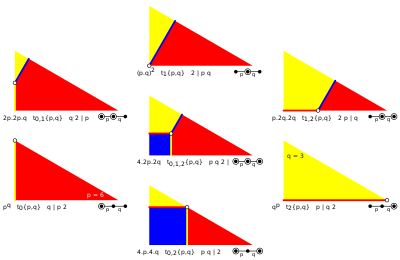
Symmetric subdivision in hyperbolic geometry
Examples of uniform tilings
Spherical
Euclidean
Hyperbolic
{5,3} {6,3} {7,3} {∞,3}
Regular tilings
t{5,3} t{6,3} t{7,3}
Truncated tilings have 2p.2p.q vertex figures from regular {p,q}.
r{5,3} r{6,3} r{7,3}
Quasiregular tilings
rr{5,3} rr{6,3} rr{7,3} rr{∞,3}
Semiregular tilings
tr{5,3} tr{6,3} tr{7,3} tr{∞,3}
Omnitruncated tilings
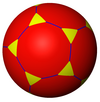
Construction of Archimedean Solids and Tessellations
Symmetry
Triangular dihedral symmetry Tetrahedral Octahedral Icosahedral p6m symmetry [3,7] symmetry [3,8] symmetry
Starting solid
Symbol
Triangular hosohedron Triangular dihedron Tetrahedron Cube Octahedron Dodecahedron Icosahedron Hexagonal tiling Triangular tiling Heptagonal tiling Order-7 triangular tiling Octagonal tiling Order-8 triangular tiling
Truncation (t)t{p,q}
triangular prism truncated triangular dihedron(Half of the "edges" count as degenerate digon faces . The other half are normal edges.)
truncated tetrahedron truncated cube truncated octahedron truncated dodecahedron truncated icosahedron Truncated hexagonal tiling Truncated triangular tiling Truncated heptagonal tiling Truncated order-7 triangular tiling Truncated octagonal tiling Truncated order-8 triangular tiling
Rectification (r)r{p,q}
tridihedron(All of the "edges" count as degenerate digon faces .)
tetratetrahedron cuboctahedron icosidodecahedron Trihexagonal tiling Triheptagonal tiling Trioctagonal tiling
Bitruncation (2t)2t{p,q}
truncated triangular dihedron(Half of the "edges" count as degenerate digon faces . The other half are normal edges.)
triangular prism
truncated tetrahedron
truncated octahedron
truncated cube
truncated icosahedron
truncated dodecahedron
truncated triangular tiling
truncated hexagonal tiling
Truncated order-7 triangular tiling
Truncated heptagonal tiling
Truncated order-8 triangular tiling
Truncated octagonal tiling
Birectification (2r)Dual (d)2r{p,q}
triangular dihedron
triangular hosohedron
tetrahedron
octahedron
cube
icosahedron
dodecahedron
triangular tiling
hexagonal tiling
Order-7 triangular tiling
Heptagonal tiling
Order-8 triangular tiling
Octagonal tiling
Cantellation (rr)Expansion (e)rr{p,q}
triangular prism (The "edge" between each pair of tetragons counts as a degenerate digon face . The other edges (the ones between a trigon and a tetragon) are normal edges.) rhombitetratetrahedron rhombicuboctahedron rhombicosidodecahedron rhombitrihexagonal tiling Rhombitriheptagonal tiling Rhombitrioctagonal tiling
Snub rectified (sr)Snub (s)
sr{p,q}
triangular antiprism (Three yellow-yellow "edges", no two of which share any vertices, count as degenerate digon faces . The other edges are normal edges.) snub tetratetrahedron snub cuboctahedron snub icosidodecahedron snub trihexagonal tiling Snub triheptagonal tiling Snub trioctagonal tiling
Cantitruncation (tr)tr{p,q}
hexagonal prism truncated tetratetrahedron truncated cuboctahedron truncated icosidodecahedron truncated trihexagonal tiling Truncated triheptagonal tiling Truncated trioctagonal tiling
In hyperbolic geometry , a uniform hyperbolic tiling (or regular, quasiregular or semiregular hyperbolic tiling) is an edge-to-edge filling of the hyperbolic plane which has regular polygons as faces and is vertex-transitive (transitive on its vertices , isogonal, i.e. there is an isometry mapping any vertex onto any other). It follows that all vertices are congruent , and the tiling has a high degree of rotational and translational symmetry .
Uniform tilings can be identified by their vertex configuration , a sequence of numbers representing the number of sides of the polygons around each vertex. For example, 7.7.7 represents the heptagonal tiling which has 3 heptagons around each vertex. It is also regular since all the polygons are the same size, so it can also be given the Schläfli symbol {7,3}.
Uniform tilings may be regular (if also face- and edge-transitive), quasi-regular (if edge-transitive but not face-transitive) or semi-regular (if neither edge- nor face-transitive). For right triangles (p q 2), there are two regular tilings, represented by Schläfli symbol {p ,q } and {q ,p }.
Wythoff construction
Example Wythoff construction with right triangles (r = 2) and the 7 generator points. Lines to the active mirrors are colored red, yellow, and blue with the 3 nodes opposite them as associated by the Wythoff symbol. There are an infinite number of uniform tilings based on the Schwarz triangles (p q r ) where 1 / p 1 / q 1 / r p , q , r are each orders of reflection symmetry at three points of the fundamental domain triangle – the symmetry group is a hyperbolic triangle group .
Each symmetry family contains 7 uniform tilings, defined by a Wythoff symbol or Coxeter-Dynkin diagram , 7 representing combinations of 3 active mirrors. An 8th represents an alternation operation, deleting alternate vertices from the highest form with all mirrors active.
Families with r = 2 contain regular hyperbolic tilings , defined by a Coxeter group such as [7,3], [8,3], [9,3], ... [5,4], [6,4], ....
Hyperbolic families with r = 3 or higher are given by (p q r ) and include (4 3 3), (5 3 3), (6 3 3) ... (4 4 3), (5 4 3), ... (4 4 4)....
Hyperbolic triangles (p q r ) define compact uniform hyperbolic tilings. In the limit any of p , q or r can be replaced by ∞ which defines a paracompact hyperbolic triangle and creates uniform tilings with either infinite faces (called apeirogons ) that converge to a single ideal point, or infinite vertex figure with infinitely many edges diverging from the same ideal point.
More symmetry families can be constructed from fundamental domains that are not triangles.
Selected families of uniform tilings are shown below (using the Poincaré disk model for the hyperbolic plane). Three of them – (7 3 2), (5 4 2), and (4 3 3) – and no others, are minimal in the sense that if any of their defining numbers is replaced by a smaller integer the resulting pattern is either Euclidean or spherical rather than hyperbolic; conversely, any of the numbers can be increased (even to infinity) to generate other hyperbolic patterns.
Each uniform tiling generates a dual uniform tiling , with many of them also given below.
Right triangle domains
There are infinitely many (p q 2) triangle group families. This article shows the regular tiling up to p , q = 8, and uniform tilings in 12 families: (7 3 2), (8 3 2), (5 4 2), (6 4 2), (7 4 2), (8 4 2), (5 5 2), (6 5 2) (6 6 2), (7 7 2), (8 6 2), and (8 8 2).
Regular hyperbolic tilings
The simplest set of hyperbolic tilings are regular tilings {p ,q }, which exist in a matrix with the regular polyhedra and Euclidean tilings. The regular tiling {p ,q } has a dual tiling {q ,p } across the diagonal axis of the table. Self-dual tilings {2,2}, {3,3} , {4,4} , {5,5} , etc. pass down the diagonal of the table.
Regular hyperbolic tiling table
Spherical (improper /Platonic) /Euclidean /hyperbolic (Poincaré disc: compact /paracompact /noncompact ) tessellations with their Schläfli symbol
p \ q
2
3
4
5
6
7
8
...
∞
...
iπ/λ
2
{2 ,2} {2,3} {2,4} {2,5} {2,6} {2,7} {2,8} {2,∞}
3
{3,2} tetrahedron )octahedron )icosahedron )deltille ){3,7} {3,8} {3,∞}
4
{4,2} cube )quadrille ){4,5} {4,6} {4,7} {4,8} {4,∞}
5
{5,2} dodecahedron ){5,4} {5,5} {5,6} {5,8} {5,∞}
6
{6,2} hextille ){6,4} {6,5} {6,6} {6,8} {6,∞}
7
{7,2} {7,3} {7,4} {7,7} {7,iπ/λ}
8
{8,2} {8,3} {8,4} {8,6} {8,8} {8,iπ/λ}
...
∞
{∞,2} {∞,3} {∞,4} {∞,5} {∞,6} {∞,∞}
...
iπ/λ
{iπ/λ,7}
{iπ/λ,8}
{iπ/λ, iπ/λ}
(7 3 2)
The (7 3 2) triangle group , Coxeter group [7,3], orbifold (*732) contains these uniform tilings:
Uniform heptagonal/triangular tilings
Symmetry: [7,3], (*732)
[7,3]+ , (732)
{7,3} t{7,3} r{7,3} t{3,7} {3,7} rr{7,3} tr{7,3} sr{7,3}
Uniform duals
V73 V3.14.14
V3.7.3.7
V6.6.7
V37 V3.4.7.4
V4.6.14 V3.3.3.3.7
(8 3 2)
The (8 3 2) triangle group , Coxeter group [8,3], orbifold (*832) contains these uniform tilings:
Uniform octagonal/triangular tilings
Symmetry: [8,3], (*832)
[8,3]+
[1+ ,8,3]
[8,3+ ]
{8,3}
t{8,3}
r{8,3}
t{3,8}
{3,8}
rr{8,3} 2 {3,8}
tr{8,3}
sr{8,3}
h{8,3}
h2 {8,3}
s{3,8}
Uniform duals
V83
V3.16.16
V3.8.3.8
V6.6.8
V38
V3.4.8.4
V4.6.16
V34 .8
V(3.4)3
V8.6.6
V35 .4
(5 4 2)
The (5 4 2) triangle group , Coxeter group [5,4], orbifold (*542) contains these uniform tilings:
Uniform pentagonal/square tilings
Symmetry: [5,4], (*542)
[5,4]+ , (542)
[5+ ,4], (5*2)
[5,4,1+ ], (*552)
{5,4}
t{5,4}
r{5,4}
2t{5,4}=t{4,5}
2r{5,4}={4,5}
rr{5,4}
tr{5,4}
sr{5,4}
s{5,4}
h{4,5}
Uniform duals
V54
V4.10.10
V4.5.4.5
V5.8.8
V45
V4.4.5.4
V4.8.10
V3.3.4.3.5
V3.3.5.3.5
V55
(6 4 2)
The (6 4 2) triangle group , Coxeter group [6,4], orbifold (*642) contains these uniform tilings. Because all the elements are even, each uniform dual tiling one represents the fundamental domain of a reflective symmetry: *3333, *662, *3232, *443, *222222, *3222, and *642 respectively. As well, all 7 uniform tiling can be alternated, and those have duals as well.
Uniform tetrahexagonal tilings
Symmetry : [6,4], (*642 )
{6,4}
t{6,4}
r{6,4}
t{4,6}
{4,6}
rr{6,4}
tr{6,4}
Uniform duals
V64
V4.12.12
V(4.6)2
V6.8.8
V46
V4.4.4.6
V4.8.12
Alternations
[1+ ,6,4]
[6+ ,4]
[6,1+ ,4]
[6,4+ ]
[6,4,1+ ]
[(6,4,2+ )]
[6,4]+
h{6,4}
s{6,4}
hr{6,4}
s{4,6}
h{4,6}
hrr{6,4}
sr{6,4}
(7 4 2)
The (7 4 2) triangle group , Coxeter group [7,4], orbifold (*742) contains these uniform tilings:
Uniform heptagonal/square tilings
Symmetry: [7,4], (*742)
[7,4]+ , (742)
[7+ ,4], (7*2)
[7,4,1+ ], (*772)
{7,4}
t{7,4}
r{7,4}
2t{7,4}=t{4,7}
2r{7,4}={4,7}
rr{7,4}
tr{7,4}
sr{7,4}
s{7,4}
h{4,7}
Uniform duals
V74
V4.14.14
V4.7.4.7
V7.8.8
V47
V4.4.7.4
V4.8.14
V3.3.4.3.7
V3.3.7.3.7
V77
(8 4 2)
The (8 4 2) triangle group , Coxeter group [8,4], orbifold (*842) contains these uniform tilings. Because all the elements are even, each uniform dual tiling one represents the fundamental domain of a reflective symmetry: *4444, *882, *4242, *444, *22222222, *4222, and *842 respectively. As well, all 7 uniform tiling can be alternated, and those have duals as well.
Uniform octagonal/square tilings
[8,4], (*842)
{8,4}
t{8,4} r{8,4}
2t{8,4}=t{4,8}
2r{8,4}={4,8}
rr{8,4}
tr{8,4}
Uniform duals
V84
V4.16.16
V(4.8)2
V8.8.8
V48
V4.4.4.8
V4.8.16
Alternations
[1+ ,8,4]
[8+ ,4]
[8,1+ ,4]
[8,4+ ]
[8,4,1+ ]
[(8,4,2+ )]
[8,4]+
h{8,4}
s{8,4}
hr{8,4}
s{4,8}
h{4,8}
hrr{8,4}
sr{8,4}
Alternation duals
V(4.4)4
V3.(3.8)2
V(4.4.4)2
V(3.4)3
V88
V4.44
V3.3.4.3.8
(5 5 2)
The (5 5 2) triangle group , Coxeter group [5,5], orbifold (*552) contains these uniform tilings:
Uniform pentapentagonal tilings
Symmetry: [5,5], (*552)
[5,5]+ , (552)
Order-5 pentagonal tiling {5,5}
Truncated order-5 pentagonal tiling t{5,5}
Order-4 pentagonal tiling r{5,5}
Truncated order-5 pentagonal tiling 2t{5,5} = t{5,5}
Order-5 pentagonal tiling 2r{5,5} = {5,5}
Tetrapentagonal tiling rr{5,5}
Truncated order-4 pentagonal tiling tr{5,5}
Snub pentapentagonal tiling sr{5,5}
Uniform duals
Order-5 pentagonal tiling V5.5.5.5.5
V5.10.10
Order-5 square tiling V5.5.5.5
V5.10.10
Order-5 pentagonal tiling V5.5.5.5.5
V4.5.4.5
V4.10.10
V3.3.5.3.5
(6 5 2)
The (6 5 2) triangle group , Coxeter group [6,5], orbifold (*652) contains these uniform tilings:
Uniform hexagonal/pentagonal tilings
Symmetry: [6,5], (*652)
[6,5]+ , (652)
[6,5+ ], (5*3)
[1+ ,6,5], (*553)
{6,5}
t{6,5}
r{6,5}
2t{6,5}=t{5,6}
2r{6,5}={5,6}
rr{6,5}
tr{6,5}
sr{6,5}
s{5,6}
h{6,5}
Uniform duals
V65
V5.12.12
V5.6.5.6
V6.10.10
V56
V4.5.4.6
V4.10.12
V3.3.5.3.6
V3.3.3.5.3.5
V(3.5)5
(6 6 2)
The (6 6 2) triangle group , Coxeter group [6,6], orbifold (*662) contains these uniform tilings:
Uniform hexahexagonal tilings
Symmetry: [6,6], (*662)
{6,6} t{6,6} 2 {4,6}
r{6,6} t{6,6} 2 {4,6}
{6,6} rr{6,6} tr{6,6}
Uniform duals
V66
V6.12.12
V6.6.6.6
V6.12.12
V66
V4.6.4.6
V4.12.12
Alternations
[1+ ,6,6]
[6+ ,6]
[6,1+ ,6]
[6,6+ ]
[6,6,1+ ]
[(6,6,2+ )]
[6,6]+
h{6,6}
s{6,6}
hr{6,6}
s{6,6}
h{6,6}
hrr{6,6}
sr{6,6}
(8 6 2)
The (8 6 2) triangle group , Coxeter group [8,6], orbifold (*862) contains these uniform tilings.
Uniform octagonal/hexagonal tilings
Symmetry : [8,6], (*862)
{8,6}
t{8,6} r{8,6}
2t{8,6}=t{6,8}
2r{8,6}={6,8}
rr{8,6}
tr{8,6}
Uniform duals
V86
V6.16.16
V(6.8)2
V8.12.12
V68
V4.6.4.8
V4.12.16
Alternations
[1+ ,8,6]
[8+ ,6]
[8,1+ ,6]
[8,6+ ]
[8,6,1+ ]
[(8,6,2+ )]
[8,6]+
h{8,6}
s{8,6}
hr{8,6}
s{6,8}
h{6,8}
hrr{8,6}
sr{8,6}
Alternation duals
V(4.6)6
V3.3.8.3.8.3
V(3.4.4.4)2
V3.4.3.4.3.6
V(3.8)8
V3.45
V3.3.6.3.8
(7 7 2)
The (7 7 2) triangle group , Coxeter group [7,7], orbifold (*772) contains these uniform tilings:
Uniform heptaheptagonal tilings
Symmetry: [7,7], (*772)
[7,7]+ , (772)
{7,7}
t{7,7} r{7,7}
2t{7,7}=t{7,7}
2r{7,7}={7,7}
rr{7,7}
tr{7,7}
sr{7,7}
Uniform duals
V77
V7.14.14
V7.7.7.7
V7.14.14
V77
V4.7.4.7
V4.14.14
V3.3.7.3.7
(8 8 2)
The (8 8 2) triangle group , Coxeter group [8,8], orbifold (*882) contains these uniform tilings:
Uniform octaoctagonal tilings
Symmetry: [8,8], (*882)
{8,8}
t{8,8} r{8,8}
2t{8,8}=t{8,8}
2r{8,8}={8,8}
rr{8,8}
tr{8,8}
Uniform duals
V88
V8.16.16
V8.8.8.8
V8.16.16
V88
V4.8.4.8
V4.16.16
Alternations
[1+ ,8,8]
[8+ ,8]
[8,1+ ,8]
[8,8+ ]
[8,8,1+ ]
[(8,8,2+ )]
[8,8]+
h{8,8}
s{8,8}
hr{8,8}
s{8,8}
h{8,8}
hrr{8,8}
sr{8,8}
Alternation duals
V(4.8)8
V3.4.3.8.3.8
V(4.4)4
V3.4.3.8.3.8
V(4.8)8
V46
V3.3.8.3.8
General triangle domains
There are infinitely many general triangle group families (p q r ). This article shows uniform tilings in 9 families: (4 3 3), (4 4 3), (4 4 4), (5 3 3), (5 4 3), (5 4 4), (6 3 3), (6 4 3), and (6 4 4).
(4 3 3)
The (4 3 3) triangle group , Coxeter group [(4,3,3)], orbifold (*433) contains these uniform tilings. Without right angles in the fundamental triangle, the Wythoff constructions are slightly different. For instance in the (4,3,3) triangle family , the snub form has six polygons around a vertex and its dual has hexagons rather than pentagons. In general the vertex figure of a snub tiling in a triangle (p ,q ,r ) is p. 3.q.3.r.3, being 4.3.3.3.3.3 in this case below.
Uniform (4,3,3) tilings
Symmetry: [(4,3,3)], (*433)
[(4,3,3)]+ , (433)
h{8,3} 0 (4,3,3)
r{3,8}1 /2 0,1 (4,3,3)
h{8,3} 1 (4,3,3)
h2 {8,3} 1,2 (4,3,3)
{3,8}1 /2 2 (4,3,3)
h2 {8,3} 0,2 (4,3,3)
t{3,8}1 /2 0,1,2 (4,3,3)
s{3,8}1 /2
Uniform duals
V(3.4)3
V3.8.3.8
V(3.4)3
V3.6.4.6
V(3.3)4
V3.6.4.6
V6.6.8
V3.3.3.3.3.4
(4 4 3)
The (4 4 3) triangle group , Coxeter group [(4,4,3)], orbifold (*443) contains these uniform tilings.
Uniform (4,4,3) tilings
Symmetry: [(4,4,3)] (*443)
[(4,4,3)]+
[(4,4,3+ )]
[(4,1+ ,4,3)]
h{6,4} 0 (4,4,3)
h2 {6,4} 0,1 (4,4,3)
{4,6}1 /2 1 (4,4,3)
h2 {6,4}1,2 (4,4,3)
h{6,4}2 (4,4,3)
r{6,4}1 /2 0,2 (4,4,3)
t{4,6}1 /2 0,1,2 (4,4,3)
s{4,6}1 /2 hr{4,6}1 /2
h{4,6}1 /2 q{4,6} 1 (4,3,4)
Uniform duals
V(3.4)4
V3.8.4.8
V(4.4)3
V3.8.4.8
V(3.4)4
V4.6.4.6
V6.8.8
V3.3.3.4.3.4
V(4.4.3)2
V66
V4.3.4.6.6
(4 4 4)
The (4 4 4) triangle group , Coxeter group [(4,4,4)], orbifold (*444) contains these uniform tilings.
Uniform (4,4,4) tilings
Symmetry: [(4,4,4)], (*444)
[(4,4,4)]+
[(1+ ,4,4,4)]
[(4+ ,4,4)]
t0 (4,4,4) t0,1 (4,4,4) 2 {8,4}
t1 (4,4,4) 1 /2
t1,2 (4,4,4) 2 {8,4}
t2 (4,4,4) t0,2 (4,4,4) 1 /2
t0,1,2 (4,4,4) 1 /2
s(4,4,4) 1 /2
h(4,4,4) 1 /2
hr(4,4,4) 1 /2
Uniform duals
V(4.4)4
V4.8.4.8
V(4.4)4
V4.8.4.8
V(4.4)4
V4.8.4.8
V8.8.8
V3.4.3.4.3.4
V88
V(4,4)3
(5 3 3)
The (5 3 3) triangle group , Coxeter group [(5,3,3)], orbifold (*533) contains these uniform tilings.
Uniform (5,3,3) tilings
Symmetry: [(5,3,3)], (*533)
[(5,3,3)]+ , (533)
h{10,3}0 (5,3,3)
r{3,10}1 /2 0,1 (5,3,3)
h{10,3}1 (5,3,3)
h2 {10,3}1,2 (5,3,3)
{3,10}1 /2 2 (5,3,3)
h2 {10,3}0,2 (5,3,3)
t{3,10}1 /2 0,1,2 (5,3,3)
s{3,10}1 /2 0,1,2 (5,3,3)
Uniform duals
V(3.5)3
V3.10.3.10
V(3.5)3
V3.6.5.6
V(3.3)5
V3.6.5.6
V6.6.10
V3.3.3.3.3.5
(5 4 3)
The (5 4 3) triangle group , Coxeter group [(5,4,3)], orbifold (*543) contains these uniform tilings.
(5,4,3) uniform tilings
Symmetry: [(5,4,3)], (*543)
[(5,4,3)]+ , (543)
t0 (5,4,3)
t0,1 (5,4,3)
t1 (5,4,3)
t1,2 (5,4,3)
t2 (5,4,3)
t0,2 (5,4,3)
t0,1,2 (5,4,3)
s(5,4,3)
Uniform duals
V(3.5)4
V3.10.4.10
V(4.5)3
V3.8.5.8
V(3.4)5
V4.6.5.6
V6.8.10
V3.5.3.4.3.3
(5 4 4)
The (5 4 4) triangle group , Coxeter group [(5,4,4)], orbifold (*544) contains these uniform tilings.
Uniform (5,4,4) tilings
Symmetry: [(5,4,4)]
[(5,4,4)]+
[(5+ ,4,4)]
[(5,4,1+ ,4)]
t0 (5,4,4)
t0,1 (5,4,4)1 /2
t1 (5,4,4)
t1,2 (5,4,4)2 {10,4}
t2 (5,4,4)1 /2
t0,2 (5,4,4)2 {10,4}
t0,1,2 (5,4,4)1 /2
s(4,5,4)1 /2
h(4,5,4)1 /2
hr(4,5,4)1 /2
Uniform duals
V(4.5)4
V4.10.4.10
V(4.5)4
V4.8.5.8
V(4.4)5
V4.8.5.8
V8.8.10
V3.4.3.4.3.5
V1010
V(4.4.5)2
(6 3 3)
The (6 3 3) triangle group , Coxeter group [(6,3,3)], orbifold (*633) contains these uniform tilings.
Uniform (6,3,3) tilings
Symmetry: [(6,3,3)], (*633)
[(6,3,3)]+ , (633)
t0 {(6,3,3)}
t0,1 {(6,3,3)}1 /2
t1 {(6,3,3)}
t1,2 {(6,3,3)}2 {12,3}
t2 {(6,3,3)}1 /2
t0,2 {(6,3,3)}2 {12,3}
t0,1,2 {(6,3,3)}1 /2
s{(6,3,3)}1 /2
Uniform duals
V(3.6)3
V3.12.3.12
V(3.6)3
V3.6.6.6
V(3.3)6
V3.6.6.6
V6.6.12
V3.3.3.3.3.6
(6 4 3)
The (6 4 3) triangle group , Coxeter group [(6,4,3)], orbifold (*643) contains these uniform tilings.
(6,4,3) uniform tilings
Symmetry: [(6,4,3)]
[(6,4,3)]+
[(6,1+ ,4,3)]
[(6,4,3+ )]
t0 {(6,4,3)}
t0,1 {(6,4,3)}
t1 {(6,4,3)}
t1,2 {(6,4,3)}
t2 {(6,4,3)}
t0,2 {(6,4,3)}
t0,1,2 {(6,4,3)}
s{(6,4,3)}
h{(6,4,3)}
hr{(6,4,3)}
Uniform duals
V(3.6)4
V3.12.4.12
V(4.6)3
V3.8.6.8
V(3.4)6
V4.6.6.6
V6.8.12
V3.6.3.4.3.3
V(3.6.6)3
V4.(3.4)3
(6 4 4)
The (6 4 4) triangle group , Coxeter group [(6,4,4)], orbifold (*644) contains these uniform tilings.
6-4-4 uniform tilings
Symmetry : [(6,4,4)], (*644)
(644)
(6,4,4)
t0,1 (6,4,4)1 /2
t1 (6,4,4)
t1,2 (6,4,4)2 {12,4}
t2 (6,4,4)1 /2
t0,2 (6,4,4)2 {12,4}
t0,1,2 (6,4,4)1 /2
s(6,4,4)1 /2
Uniform duals
V(4.6)4
V(4.12)2
V(4.6)4
V4.8.6.8
V412
V4.8.6.8
V8.8.12
V4.6.4.6.6.6
Summary of tilings with finite triangular fundamental domains
For a table of all uniform hyperbolic tilings with fundamental domains (p q r ), where 2 ≤ p ,q ,r ≤ 8.
See Template:Finite triangular hyperbolic tilings table
Ideal triangle domains
There are infinitely many triangle group families including infinite orders. This article shows uniform tilings in 9 families: (∞ 3 2), (∞ 4 2), (∞ ∞ 2), (∞ 3 3), (∞ 4 3), (∞ 4 4), (∞ ∞ 3), (∞ ∞ 4), and (∞ ∞ ∞).
(∞ 3 2)
The ideal (∞ 3 2) triangle group , Coxeter group [∞,3], orbifold (*∞32) contains these uniform tilings:
Paracompact uniform tilings in [∞,3] family
Symmetry: [∞,3], (*∞32)
[∞,3]+
[1+ ,∞,3]
[∞,3+ ]
{∞,3}
t{∞,3}
r{∞,3}
t{3,∞}
{3,∞}
rr{∞,3}
tr{∞,3}
sr{∞,3}
h{∞,3}
h2 {∞,3}
s{3,∞}
Uniform duals
V∞3
V3.∞.∞
V(3.∞)2
V6.6.∞
V3∞
V4.3.4.∞
V4.6.∞
V3.3.3.3.∞
V(3.∞)3
V3.3.3.3.3.∞
(∞ 4 2)
The ideal (∞ 4 2) triangle group , Coxeter group [∞,4], orbifold (*∞42) contains these uniform tilings:
Paracompact uniform tilings in [∞,4] family
{∞,4}
t{∞,4}
r{∞,4}
2t{∞,4}=t{4,∞}
2r{∞,4}={4,∞}
rr{∞,4}
tr{∞,4}
Dual figures
V∞4
V4.∞.∞
V(4.∞)2
V8.8.∞
V4∞
V43 .∞
V4.8.∞
Alternations
[1+ ,∞,4]
[∞+ ,4]
[∞,1+ ,4]
[∞,4+ ]
[∞,4,1+ ]
[(∞,4,2+ )]
[∞,4]+
h{∞,4}
s{∞,4}
hr{∞,4}
s{4,∞}
h{4,∞}
hrr{∞,4}
s{∞,4}
Alternation duals
V(∞.4)4
V3.(3.∞)2
V(4.∞.4)2
V3.∞.(3.4)2
V∞∞
V∞.44
V3.3.4.3.∞
(∞ 5 2)
The ideal (∞ 5 2) triangle group , Coxeter group [∞,5], orbifold (*∞52) contains these uniform tilings:
Paracompact uniform apeirogonal/pentagonal tilings
Symmetry: [∞,5], (*∞52)
[∞,5]+
[1+ ,∞,5]
[∞,5+ ]
{∞,5}
t{∞,5}
r{∞,5}
2t{∞,5}=t{5,∞}
2r{∞,5}={5,∞}
rr{∞,5}
tr{∞,5}
sr{∞,5}
h{∞,5}
h2 {∞,5}
s{5,∞}
Uniform duals
V∞5
V5.∞.∞
V5.∞.5.∞
V∞.10.10
V5∞
V4.5.4.∞
V4.10.∞
V3.3.5.3.∞
V(∞.5)5
V3.5.3.5.3.∞
(∞ ∞ 2)
The ideal (∞ ∞ 2) triangle group , Coxeter group [∞,∞], orbifold (*∞∞2) contains these uniform tilings:
Paracompact uniform tilings in [∞,∞] family
{∞,∞}
t{∞,∞}
r{∞,∞}
2t{∞,∞}=t{∞,∞}
2r{∞,∞}={∞,∞}
rr{∞,∞}
tr{∞,∞}
Dual tilings
V∞∞
V∞.∞.∞
V(∞.∞)2
V∞.∞.∞
V∞∞
V4.∞.4.∞
V4.4.∞
Alternations
[1+ ,∞,∞]
[∞+ ,∞]
[∞,1+ ,∞]
[∞,∞+ ]
[∞,∞,1+ ]
[(∞,∞,2+ )]
[∞,∞]+
h{∞,∞}
s{∞,∞}
hr{∞,∞}
s{∞,∞}
h2 {∞,∞}
hrr{∞,∞}
sr{∞,∞}
Alternation duals
V(∞.∞)∞
V(3.∞)3
V(∞.4)4
V(3.∞)3
V∞∞
V(4.∞.4)2
V3.3.∞.3.∞
(∞ 3 3)
The ideal (∞ 3 3) triangle group , Coxeter group [(∞,3,3)], orbifold (*∞33) contains these uniform tilings.
Paracompact hyperbolic uniform tilings in [(∞,3,3)] family
Symmetry: [(∞,3,3)], (*∞33)
[(∞,3,3)]+ , (∞33)
(∞,∞,3)
t 0,1 (∞,3,3)
t1 (∞,3,3)
t1,2 (∞,3,3)
t2 (∞,3,3)
t0,2 (∞,3,3)
t0,1,2 (∞,3,3)
s(∞,3,3)
Dual tilings
V(3.∞)3
V3.∞.3.∞
V(3.∞)3
V3.6.∞.6
V(3.3)∞
V3.6.∞.6
V6.6.∞
V3.3.3.3.3.∞
(∞ 4 3)
The ideal (∞ 4 3) triangle group , Coxeter group [(∞,4,3)], orbifold (*∞43) contains these uniform tilings:
Paracompact hyperbolic uniform tilings in [(∞,4,3)] family
Symmetry: [(∞,4,3)]
[(∞,4,3)]+
[(∞,4,3+ )]
[(∞,1+ ,4,3)]
(∞,4,3)
t 0,1 (∞,4,3)
t1 (∞,4,3)
t1,2 (∞,4,3)
t2 (∞,4,3)
t0,2 (∞,4,3)
t0,1,2 (∞,4,3)
s(∞,4,3)
ht0,2 (∞,4,3)
ht1 (∞,4,3)
Dual tilings
V(3.∞)4
V3.∞.4.∞
V(4.∞)3
V3.8.∞.8
V(3.4)∞
4.6.∞.6
V6.8.∞
V3.3.3.4.3.∞
V(4.3.4)2 .∞
V(6.∞.6)3
(∞ 4 4)
The ideal (∞ 4 4) triangle group , Coxeter group [(∞,4,4)], orbifold (*∞44) contains these uniform tilings.
Paracompact hyperbolic uniform tilings in [(4,4,∞)] family
Symmetry: [(4,4,∞)], (*44∞)
(44∞)
(4,4,∞)
t 0,1 (4,4,∞)1 /2
t1 (4,4,∞)1 /2
t1,2 (4,4,∞)2 {∞,4}
t2 (4,4,∞){4,∞}1 /2
t0,2 (4,4,∞)2 {∞,4}
t0,1,2 (4,4,∞)t{4,∞}1 /2
s(4,4,∞)1 /2
Dual tilings
V(4.∞)4
V4.∞.4.∞
V(4.∞)4
V4.∞.4.∞
V4∞
V4.∞.4.∞
V8.8.∞
V3.4.3.4.3.∞
(∞ ∞ 3)
The ideal (∞ ∞ 3) triangle group , Coxeter group [(∞,∞,3)], orbifold (*∞∞3) contains these uniform tilings.
Paracompact hyperbolic uniform tilings in [(∞,∞,3)] family
Symmetry: [(∞,∞,3)], (*∞∞3)
[(∞,∞,3)]+
[(∞,∞,3+ )]
[(∞,1+ ,∞,3)]
(∞,∞,3)
t 0,1 (∞,∞,3)2 {6,∞}
t1 (∞,∞,3)1 /2
t1,2 (∞,∞,3)2 {6,∞}
t2 (∞,∞,3)
t0,2 (∞,∞,3)1 /2
t0,1,2 (∞,∞,3)1 /2
s(∞,∞,3)1 /2
hr0,2 (∞,∞,3)1 /2
hr1 (∞,∞,3)1 /2
Dual tilings
V(3.∞)∞
V3.∞.∞.∞
V(∞.∞)3
V3.∞.∞.∞
V(3.∞)∞
V(6.∞)2
V6.∞.∞
V3.∞.3.∞.3.3
V(3.4.∞.4)2
V(∞.6)6
(∞ ∞ 4)
The ideal (∞ ∞ 4) triangle group , Coxeter group [(∞,∞,4)], orbifold (*∞∞4) contains these uniform tilings.
Paracompact hyperbolic uniform tilings in [(∞,∞,4)] family
Symmetry: [(∞,∞,4)], (*∞∞4)
(∞,∞,4)
t 0,1 (∞,∞,4)2 {8,∞}
t1 (∞,∞,4)
t1,2 (∞,∞,4)2 {∞,8}
t2 (∞,∞,4)
t0,2 (∞,∞,4)
t0,1,2 (∞,∞,4)
Dual tilings
V(4.∞)∞
V∞.∞.∞.4
V∞4
V∞.∞.∞.4
V(4.∞)∞
V∞.∞.∞.4
V∞.∞.8
Alternations
[(1+ ,∞,∞,4)]
[(∞+ ,∞,4)]
[(∞,1+ ,∞,4)]
[(∞,∞+ ,4)]
[(∞,∞,1+ ,4)]
[(∞,∞,4+ )]
[(∞,∞,4)]+
Alternation duals
V∞∞
V∞.44
V(∞.4)4
V∞.44
V∞∞
V∞.44
V3.∞.3.∞.3.4
(∞ ∞ ∞)
The ideal (∞ ∞ ∞) triangle group , Coxeter group [(∞,∞,∞)], orbifold (*∞∞∞) contains these uniform tilings.
Paracompact uniform tilings in [(∞,∞,∞)] family
(∞,∞,∞) r(∞,∞,∞) 2 {∞,∞}
(∞,∞,∞) r(∞,∞,∞) 2 {∞,∞}
(∞,∞,∞) r(∞,∞,∞) t(∞,∞,∞)
Dual tilings
V∞∞
V∞.∞.∞.∞
V∞∞
V∞.∞.∞.∞
V∞∞
V∞.∞.∞.∞
V∞.∞.∞
Alternations
[(1+ ,∞,∞,∞)]
[∞+ ,∞,∞)]
[∞,1+ ,∞,∞)]
[∞,∞+ ,∞)]
[(∞,∞,∞,1+ )]
[(∞,∞,∞+ )]
[∞,∞,∞)]+
Alternation duals
V(∞.∞)∞
V(∞.4)4
V(∞.∞)∞
V(∞.4)4
V(∞.∞)∞
V(∞.4)4
V3.∞.3.∞.3.∞
Summary of tilings with infinite triangular fundamental domains
For a table of all uniform hyperbolic tilings with fundamental domains (p q r ), where 2 ≤ p ,q ,r ≤ 8, and one or more as ∞.
Infinite triangular hyperbolic tilings
(p q r)
t0
h0
t01
h01
t1
h1
t12
h12
t2
h2
t02
h02
t012
s
t0 {∞,3} 3 h0 {∞,3}3
t01 {∞,3} t1 {∞,3}2
t12 {∞,3} h12 {∞,3}
t2 {∞,3} ∞ t02 {∞,3} t012 {∞,3} s{∞,3}
t0 {∞,4} 4 h0 {∞,4}4
t01 {∞,4} h01 {∞,4}
t1 {∞,4}2
h1 {∞,4}2
t12 {∞,4} h12 {∞,4}
t2 {∞,4} ∞ h2 {∞,4}∞
t02 {∞,4} h02 {∞,4}
t012 {∞,4} s{∞,4}
t0 {∞,5} 5 h0 {∞,5}5
t01 {∞,5}
t1 {∞,5}2
t12 {∞,5}
h12 {∞,5}
t2 {∞,5} ∞ t02 {∞,5}
t012 {∞,5}
s{∞,5}
t0 {∞,6} 6 h0 {∞,6}6
t01 {∞,6}
h01 {∞,6}
t1 {∞,6}2
h1 {∞,6}2
t12 {∞,6}
h12 {∞,6}
t2 {∞,6} ∞ h2 {∞,6}∞
t02 {∞,6}
h02 {∞,6}
t012 {∞,6}
s{∞,6}
t0 {∞,7}7
h0 {∞,7}7
t01 {∞,7}
t1 {∞,7}2
t12 {∞,7}
h12 {∞,7}
t2 {∞,7}∞
t02 {∞,7}
t012 {∞,7}
s{∞,7}
t0 {∞,8}8
h0 {∞,8}8
t01 {∞,8}
h01 {∞,8}
t1 {∞,8}2
h1 {∞,8}2
t12 {∞,8}
h12 {∞,8}
t2 {∞,8}∞
h2 {∞,8}∞
t02 {∞,8}
h02 {∞,8}
t012 {∞,8}
s{∞,8}
t0 {∞,∞} ∞ h0 {∞,∞}∞
t01 {∞,∞}
h01 {∞,∞}
t1 {∞,∞}4
h1 {∞,∞}4
t12 {∞,∞}
h12 {∞,∞}
t2 {∞,∞} ∞ h2 {∞,∞}∞
t02 {∞,∞}2
h02 {∞,∞}2
t012 {∞,∞} s{∞,∞}
t0 (∞,3,3)3
t01 (∞,3,3)2
t1 (∞,3,3)3
t12 (∞,3,3)
t2 (∞,3,3)∞
t02 (∞,3,3)
t012 (∞,3,3)
s(∞,3,3)
t0 (∞,4,3)4
t01 (∞,4,3)
t1 (∞,4,3)3
h1 (∞,4,3)3
t12 (∞,4,3)
t2 (∞,4,3)∞
t02 (∞,4,3)
h02 (∞,4,3)
t012 (∞,4,3)
s(∞,4,3)
t0 (∞,5,3)5
t01 (∞,5,3)
t1 (∞,5,3)3
t12 (∞,5,3)
t2 (∞,5,3)∞
t02 (∞,5,3)
t012 (∞,5,3)
s(∞,5,3)
t0 (∞,6,3)6
t01 (∞,6,3)
t1 (∞,6,3)3
h1 (∞,6,3)3
t12 (∞,6,3)
t2 (∞,6,3)∞
t02 (∞,6,3)
h02 (∞,6,3)
t012 (∞,6,3)
s(∞,6,3)
t0 (∞,7,3)7
t01 (∞,7,3)
t1 (∞,7,3)3
t12 (∞,7,3)
t2 (∞,7,3)∞
t02 (∞,7,3)
t012 (∞,7,3)
s(∞,7,3)
t0 (∞,8,3)8
t01 (∞,8,3)
t1 (∞,8,3)3
h1 (∞,8,3)3
t12 (∞,8,3)
t2 (∞,8,3)∞
t02 (∞,8,3)
h02 (∞,8,3)
t012 (∞,8,3)
s(∞,8,3)
t0 (∞,∞,3)∞
t01 (∞,∞,3)
t1 (∞,∞,3)6
h1 (∞,∞,3)6
t12 (∞,∞,3)
t2 (∞,∞,3)∞
t02 (∞,∞,3)2
h02 (∞,∞,3)2
t012 (∞,∞,3)
s(∞,∞,3)
t0 (∞,4,4)4
h0 (∞,4,4)4
t01 (∞,4,4)2
h01 (∞,4,4)2
t1 (∞,4,4)4
h1 (∞,4,4)4
t12 (∞,4,4)
h12 (∞,4,4)
t2 (∞,4,4)∞
h2 (∞,4,4)∞
t02 (∞,4,4)
h02 (∞,4,4)
t012 (∞,4,4)
s(∞,4,4)
t0 (∞,5,4)5
h0 (∞,5,4)5
t01 (∞,5,4)
t1 (∞,5,4)4
t12 (∞,5,4)
h12 (∞,5,4)
t2 (∞,5,4)∞
t02 (∞,5,4)
t012 (∞,5,4)
s(∞,5,4)
t0 (∞,6,4)6
h0 (∞,6,4)6
t01 (∞,6,4)
h01 (∞,6,4)
t1 (∞,6,4)4
h1 (∞,6,4)4
t12 (∞,6,4)
h12 (∞,6,4)
t2 (∞,6,4)∞
h2 (∞,6,4)∞
t02 (∞,6,4)
h02 (∞,6,4)
t012 (∞,6,4)
s(∞,6,4)
t0 (∞,7,4)7
h0 (∞,7,4)7
t01 (∞,7,4)
t1 (∞,7,4)4
t12 (∞,7,4)
h12 (∞,7,4)
t2 (∞,7,4)∞
t02 (∞,7,4)
t012 (∞,7,4)
s(∞,7,4)
t0 (∞,8,4)8
h0 (∞,8,4)8
t01 (∞,8,4)
h01 (∞,8,4)
t1 (∞,8,4)4
h1 (∞,8,4)4
t12 (∞,8,4)
h12 (∞,8,4)
t2 (∞,8,4)∞
h2 (∞,8,4)∞
t02 (∞,8,4)
h02 (∞,8,4)
t012 (∞,8,4)
s(∞,8,4)
t0 (∞,∞,4)∞
h0 (∞,∞,4)∞
t01 (∞,∞,4)
h01 (∞,∞,4)
t1 (∞,∞,4)8
h1 (∞,∞,4)8
t12 (∞,∞,4)
h12 (∞,∞,4)
t2 (∞,∞,4)∞
h2 (∞,∞,4)∞
t02 (∞,∞,4)2
h02 (∞,∞,4)2
t012 (∞,∞,4)
s(∞,∞,4)
t0 (∞,5,5)5
t01 (∞,5,5)2
t1 (∞,5,5)5
t12 (∞,5,5)
t2 (∞,5,5)∞
t02 (∞,5,5)
t012 (∞,5,5)
s(∞,5,5)
t0 (∞,6,5)6
t01 (∞,6,5)
t1 (∞,6,5)5
h1 (∞,6,5)5
t12 (∞,6,5)
t2 (∞,6,5)∞
t02 (∞,6,5)
h02 (∞,6,5)
t012 (∞,6,5)
s(∞,6,5)
t0 (∞,7,5)7
t01 (∞,7,5)
t1 (∞,7,5)5
t12 (∞,7,5)
t2 (∞,7,5)∞
t02 (∞,7,5)
t012 (∞,7,5)
s(∞,7,5)
t0 (∞,8,5)8
t01 (∞,8,5)
t1 (∞,8,5)5
h1 (∞,8,5)5
t12 (∞,8,5)
t2 (∞,8,5)∞
t02 (∞,8,5)
h02 (∞,8,5)
t012 (∞,8,5)
s(∞,8,5)
t0 (∞,∞,5)∞
t01 (∞,∞,5)
t1 (∞,∞,5)10
h1 (∞,∞,5)10
t12 (∞,∞,5)
t2 (∞,∞,5)∞
t02 (∞,∞,5)2
h02 (∞,∞,5)2
t012 (∞,∞,5)
s(∞,∞,5)
t0 (∞,6,6)6
h0 (∞,6,6)6
t01 (∞,6,6)2
h01 (∞,6,6)2
t1 (∞,6,6)6
h1 (∞,6,6)6
t12 (∞,6,6)
h12 (∞,6,6)
t2 (∞,6,6)∞
h2 (∞,6,6)∞
t02 (∞,6,6)
h02 (∞,6,6)
t012 (∞,6,6)
s(∞,6,6)
t0 (∞,7,6)7
h0 (∞,7,6)7
t01 (∞,7,6)
t1 (∞,7,6)6
t12 (∞,7,6)
h12 (∞,7,6)
t2 (∞,7,6)∞
t02 (∞,7,6)
t012 (∞,7,6)
s(∞,7,6)
t0 (∞,8,6)8
h0 (∞,8,6)8
t01 (∞,8,6)
h01 (∞,8,6)
t1 (∞,8,6)6
h1 (∞,8,6)6
t12 (∞,8,6)
h12 (∞,8,6)
t2 (∞,8,6)∞
h2 (∞,8,6)∞
t02 (∞,8,6)
h02 (∞,8,6)
t012 (∞,8,6)
s(∞,8,6)
t0 (∞,∞,6)∞
h0 (∞,∞,6)∞
t01 (∞,∞,6)
h01 (∞,∞,6)
t1 (∞,∞,6)12
h1 (∞,∞,6)12
t12 (∞,∞,6)
h12 (∞,∞,6)
t2 (∞,∞,6)∞
h2 (∞,∞,6)∞
t02 (∞,∞,6)2
h02 (∞,∞,6)2
t012 (∞,∞,6)
s(∞,∞,6)
t0 (∞,7,7)7
t01 (∞,7,7)2
t1 (∞,7,7)7
t12 (∞,7,7)
t2 (∞,7,7)∞
t02 (∞,7,7)
t012 (∞,7,7)
s(∞,7,7)
t0 (∞,8,7)8
t01 (∞,8,7)
t1 (∞,8,7)7
h1 (∞,8,7)7
t12 (∞,8,7)
t2 (∞,8,7)∞
t02 (∞,8,7)
h02 (∞,8,7)
t012 (∞,8,7)
s(∞,8,7)
t0 (∞,∞,7)∞
t01 (∞,∞,7)
t1 (∞,∞,7)14
h1 (∞,∞,7)14
t12 (∞,∞,7)
t2 (∞,∞,7)∞
t02 (∞,∞,7)2
h02 (∞,∞,7)2
t012 (∞,∞,7)
s(∞,∞,7)
t0 (∞,8,8)8
h0 (∞,8,8)8
t01 (∞,8,8)2
h01 (∞,8,8)2
t1 (∞,8,8)8
h1 (∞,8,8)8
t12 (∞,8,8)
h12 (∞,8,8)
t2 (∞,8,8)∞
h2 (∞,8,8)∞
t02 (∞,8,8)
h02 (∞,8,8)
t012 (∞,8,8)
s(∞,8,8)
t0 (∞,∞,8)∞
h0 (∞,∞,8)∞
t01 (∞,∞,8)
h01 (∞,∞,8)
t1 (∞,∞,8)16
h1 (∞,∞,8)16
t12 (∞,∞,8)
h12 (∞,∞,8)
t2 (∞,∞,8)∞
h2 (∞,∞,8)∞
t02 (∞,∞,8)2
h02 (∞,∞,8)2
t012 (∞,∞,8)
s(∞,∞,8)
t0 (∞,∞,∞)∞
h0 (∞,∞,∞)∞
t01 (∞,∞,∞)2
h01 (∞,∞,∞)2
t1 (∞,∞,∞)∞
h1 (∞,∞,∞)∞
t12 (∞,∞,∞)2
h12 (∞,∞,∞)2
t2 (∞,∞,∞)∞
h2 (∞,∞,∞)∞
t02 (∞,∞,∞)2
h02 (∞,∞,∞)2
t012 (∞,∞,∞)3
s(∞,∞,∞)3





































 (Half of the "edges" count as degenerate digon faces. The other half are normal edges.)
(Half of the "edges" count as degenerate digon faces. The other half are normal edges.)









 (All of the "edges" count as degenerate digon faces.)
(All of the "edges" count as degenerate digon faces.)



 (Half of the "edges" count as degenerate digon faces. The other half are normal edges.)
(Half of the "edges" count as degenerate digon faces. The other half are normal edges.)




















 (The "edge" between each pair of tetragons counts as a degenerate digon face. The other edges (the ones between a trigon and a tetragon) are normal edges.)
(The "edge" between each pair of tetragons counts as a degenerate digon face. The other edges (the ones between a trigon and a tetragon) are normal edges.)





 (Three yellow-yellow "edges", no two of which share any vertices, count as degenerate digon faces. The other edges are normal edges.)
(Three yellow-yellow "edges", no two of which share any vertices, count as degenerate digon faces. The other edges are normal edges.)