Polyhedron with 2 faces
A dihedron is a type of polyhedron, made of two polygon faces which share the same set of n edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q).[1] Dihedra have also been called bihedra,[2] flat polyhedra,[3] or doubly covered polygons.[3]
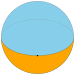
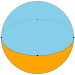
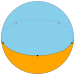
As a spherical tiling, a dihedron can exist as nondegenerate form, with two n-sided faces covering the sphere, each face being a hemisphere, and vertices on a great circle. It is regular if the vertices are equally spaced.
The dual of an n-gonal dihedron is an n-gonal hosohedron, where n digon faces share two vertices.
As a flat-faced polyhedron
A dihedron can be considered a degenerate prism whose two (planar) n-sided polygon bases are connected "back-to-back", so that the resulting object has no depth. The polygons must be congruent, but glued in such a way that one is the mirror image of the other. This applies only if the distance between the two faces is zero; for a distance larger than zero, the faces are infinite polygons (a bit like the apeirogonal hosohedron's digon faces, having a width larger than zero, are infinite stripes).
Dihedra can arise from Alexandrov's uniqueness theorem, which characterizes the distances on the surface of any convex polyhedron as being locally Euclidean except at a finite number of points with positive angular defect summing to 4π. This characterization holds also for the distances on the surface of a dihedron, so the statement of Alexandrov's theorem requires that dihedra be considered as convex polyhedra.[4]
Some dihedra can arise as lower limit members of other polyhedra families: a prism with digon bases would be a square dihedron, and a pyramid with a digon base would be a triangular dihedron.
A regular dihedron, with Schläfli symbol {n,2}, is made of two regular polygons, each with Schläfli symbol {n}.[5]
As a tiling of the sphere
A spherical dihedron is made of two spherical polygons which share the same set of n vertices, on a great circle equator; each polygon of a spherical dihedron fills a hemisphere.
A regular spherical dihedron is made of two regular spherical polygons which share the same set of n vertices, equally spaced on a great circle equator.
The regular polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.
Apeirogonal dihedron
As n tends to infinity, an n-gonal dihedron becomes an apeirogonal dihedron as a 2-dimensional tessellation:

Ditopes
A regular ditope is an n-dimensional analogue of a dihedron, with Schläfli symbol {p,...,q,r,2}. It has two facets, {p,...,q,r}, which share all ridges, {p,...,q} in common.[6]