Selected point groups in three dimensions

Involutional symmetry
Cs, (*)
[ ] = 
|

Cyclic symmetry
Cnv, (*nn)
[n] =   
|

Dihedral symmetry
Dnh, (*n22)
[n,2] =     
|
| Polyhedral group, [n,3], (*n32)
|

Tetrahedral symmetry
Td, (*332)
[3,3] =     
|

Octahedral symmetry
Oh, (*432)
[4,3] =     
|

Icosahedral symmetry
Ih, (*532)
[5,3] =     
|
Finite spherical symmetry groups are also called point groups in three dimensions. There are five fundamental symmetry classes which have triangular fundamental domains: dihedral, cyclic, tetrahedral, octahedral, and icosahedral symmetry.
This article lists the groups by Schoenflies notation, Coxeter notation,[1] orbifold notation,[2] and order. John Conway uses a variation of the Schoenflies notation, based on the groups' quaternion algebraic structure, labeled by one or two upper case letters, and whole number subscripts. The group order is defined as the subscript, unless the order is doubled for symbols with a plus or minus, "±", prefix, which implies a central inversion.[3]
Hermann–Mauguin notation (International notation) is also given. The crystallography groups, 32 in total, are a subset with element orders 2, 3, 4 and 6.[4]
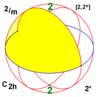
Involutional symmetry
There are four involutional groups: no symmetry (C1), reflection symmetry (Cs), 2-fold rotational symmetry (C2), and central point symmetry (Ci).
Cyclic symmetry
There are four infinite cyclic symmetry families, with n = 2 or higher. (n may be 1 as a special case as no symmetry)
| Intl
|
Geo
|
Orbifold
|
Schönflies
|
Conway
|
Coxeter
|
Order
|
Abstract
|
Fund.
domain
|
2
3
4
5
6
n
|
2
3
4
5
6
n
|
22
33
44
55
66
nn
|
C2
C3
C4
C5
C6
Cn
|
C2
C3
C4
C5
C6
Cn
|
[2]+
[3]+
[4]+
[5]+
[6]+
[n]+ |
  
  
  
  
  
  
|
2
3
4
5
6
n
|
Z2
Z3
Z4
Z5
Z6
Zn
|

|
2mm
3m
4mm
5m
6mm
nm (n is odd)
nmm (n is even)
|
2
3
4
5
6
n
|
*22
*33
*44
*55
*66
*nn
|
C2v
C3v
C4v
C5v
C6v
Cnv
|
CD4
CD6
CD8
CD10
CD12
CD2n
|
[2]
[3]
[4]
[5]
[6]
[n] |
  
  
  
  
  
  
|
4
6
8
10
12
2n
|
D4
D6
D8
D10
D12
D2n
|

|
3
8
5
12
-
|
62
82
10.2
12.2
2n.2
|
3×
4×
5×
6×
n×
|
S6
S8
S10
S12
S2n
|
±C3
CC8
±C5
CC12
CC2n / ±Cn
|
[2+,6+]
[2+,8+]
[2+,10+]
[2+,12+]
[2+,2n+] |
    
    
    
    
|
6
8
10
12
2n
|
Z6
Z8
Z10
Z12
Z2n
|

|
3/m=6
4/m
5/m=10
6/m
n/m
|
32
42
52
62
n2
|
3*
4*
5*
6*
n*
|
C3h
C4h
C5h
C6h
Cnh
|
CC6
±C4
CC10
±C6
±Cn / CC2n
|
[2,3+]
[2,4+]
[2,5+]
[2,6+]
[2,n+] |
    
    
    
    
    
|
6
8
10
12
2n
|
Z6
Z2×Z4
Z10
Z2×Z6
Z2×Zn
≅Z2n (odd n)
|

|
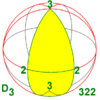
Dihedral symmetry
There are three infinite dihedral symmetry families, with n = 2 or higher (n may be 1 as a special case).
| Intl
|
Geo
|
Orbifold
|
Schönflies
|
Conway
|
Coxeter
|
Order
|
Abstract
|
Fund.
domain
|
32
422
52
622
|
3.2
4.2
5.2
6.2
n.2
|
223
224
225
226
22n
|
D3
D4
D5
D6
Dn
|
D6
D8
D10
D12
D2n
|
[2,3]+
[2,4]+
[2,5]+
[2,6]+
[2,n]+ |
    
    
    
    
    
|
6
8
10
12
2n
|
D6
D8
D10
D12
D2n
|
|
3m
82m
5m
12.2m
|
62
82
10.2
12.2
n2
|
2*3
2*4
2*5
2*6
2*n
|
D3d
D4d
D5d
D6d
Dnd
|
±D6
DD16
±D10
DD24
DD4n / ±D2n
|
[2+,6]
[2+,8]
[2+,10]
[2+,12]
[2+,2n] |
    
    
    
    
     
|
12
16
20
24
4n
|
D12
D16
D20
D24
D4n
|

|
6m2
4/mmm
10m2
6/mmm
|
32
42
52
62
n2
|
*223
*224
*225
*226
*22n
|
D3h
D4h
D5h
D6h
Dnh
|
DD12
±D8
DD20
±D12
±D2n / DD4n
|
[2,3]
[2,4]
[2,5]
[2,6]
[2,n] |
    
    
    
    
    
|
12
16
20
24
4n
|
D12
Z2×D8
D20
Z2×D12
Z2×D2n
≅D4n (odd n)
|

|
Polyhedral symmetry
There are three types of polyhedral symmetry: tetrahedral symmetry, octahedral symmetry, and icosahedral symmetry, named after the triangle-faced regular polyhedra with these symmetries.
Continuous symmetries
All of the discrete point symmetries are subgroups of certain continuous symmetries. They can be classified as products of orthogonal groups O(n) or special orthogonal groups SO(n). O(1) is a single orthogonal reflection, dihedral symmetry order 2, Dih1. SO(1) is just the identity. Half turns, C2, are needed to complete.
| Rank 3 groups |
Other names |
Example geometry |
Example finite subgroups
|
| O(3) |
|
Full symmetry of the sphere |
 |
[3,3] =      , [4,3] = , [4,3] =      , [5,3] = , [5,3] =     
[4,3+] =     
|
| SO(3) |
Sphere group |
Rotational symmetry |
[3,3]+ =      , [4,3]+ = , [4,3]+ =      , [5,3]+ = , [5,3]+ =     
|
O(2)×O(1)
O(2)⋊C2 |
Dih∞×Dih1
Dih∞⋊C2 |
Full symmetry of a spheroid, torus, cylinder, bicone or hyperboloid
Full circular symmetry with half turn |
     |
[p,2] = [p]×[ ] =     
[2p,2+] =       , [2p+,2+] = , [2p+,2+] =      
|
| SO(2)×O(1) |
C∞×Dih1 |
Rotational symmetry with reflection |
[p+,2] = [p]+×[ ] =     
|
| SO(2)⋊C2 |
C∞⋊C2 |
Rotational symmetry with half turn |
[p,2]+ =     
|
| O(2)×SO(1) |
Dih∞
Circular symmetry |
Full symmetry of a hemisphere, cone, paraboloid
or any surface of revolution |
 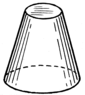   |
[p,1] = [p] =   
|
| SO(2)×SO(1) |
C∞
Circle group |
Rotational symmetry |
[p,1]+ = [p]+ =   
|