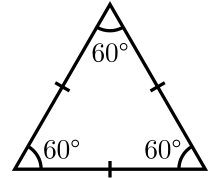
| Equilateral triangle | |
|---|---|
 | |
| Type | Regular polygon |
| Edges and vertices | 3 |
| Schläfli symbol | {3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | D3 |
| Area | |
| Internal angle (degrees) | 60° |
In geometry, an equilateral triangle is a triangle in which all three sides have the same length. In the familiar Euclidean geometry, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
Principal properties
[edit]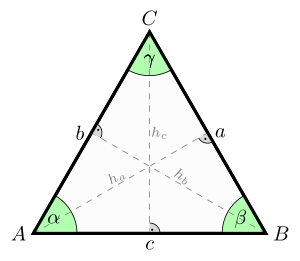
Denoting the common length of the sides of the equilateral triangle as , we can determine using the Pythagorean theorem that:
- The area is
- The perimeter is
- The radius of the circumscribed circle is
- The radius of the inscribed circle is or
- The geometric center of the triangle is the center of the circumscribed and inscribed circles
- The altitude (height) from any side is
Denoting the radius of the circumscribed circle as R, we can determine using trigonometry that:
- The area of the triangle is
Many of these quantities have simple relationships to the altitude ("h") of each vertex from the opposite side:
- The area is
- The height of the center from each side, or apothem, is
- The radius of the circle circumscribing the three vertices is
- The radius of the inscribed circle is
In an equilateral triangle, the altitudes, the angle bisectors, the perpendicular bisectors, and the medians to each side coincide.
Characterizations
[edit]A triangle that has the sides , , , semiperimeter , area , exradii , , (tangent to , , respectively), and where and are the radii of the circumcircle and incircle respectively, is equilateral if and only if any one of the statements in the following nine categories is true. Thus these are properties that are unique to equilateral triangles, and knowing that any one of them is true directly implies that we have an equilateral triangle.
Sides
[edit]Semiperimeter
[edit]Angles
[edit]Area
[edit]Circumradius, inradius, and exradii
[edit]Equal cevians
[edit]Three kinds of cevians coincide, and are equal, for (and only for) equilateral triangles:[7]
- The three altitudes have equal lengths.
- The three medians have equal lengths.
- The three angle bisectors have equal lengths.
Coincident triangle centers
[edit]Every triangle center of an equilateral triangle coincides with its centroid, which implies that the equilateral triangle is the only triangle with no Euler line connecting some of the centers. For some pairs of triangle centers, the fact that they coincide is enough to ensure that the triangle is equilateral. In particular:
- A triangle is equilateral if any two of the circumcenter, incenter, centroid, or orthocenter coincide.[8]: p.37
- It is also equilateral if its circumcenter coincides with the Nagel point, or if its incenter coincides with its nine-point center.[6]
Six triangles formed by partitioning by the medians
[edit]For any triangle, the three medians partition the triangle into six smaller triangles.
- A triangle is equilateral if and only if any three of the smaller triangles have either the same perimeter or the same inradius.[9]: Theorem 1
- A triangle is equilateral if and only if the circumcenters of any three of the smaller triangles have the same distance from the centroid.[9]: Corollary 7
Points in the plane
[edit]- A triangle is equilateral if and only if, for every point in the plane, with distances , , and to the triangle's sides and distances , , and to its vertices,[10]: p.178, #235.4
Notable theorems
[edit]
- Nearest distances from point P to sides of equilateral triangle are shown.
- Lines , , and parallel to , and , respectively, define smaller triangles , and .
- As these triangles are equilateral, their altitudes can be rotated to be vertical.
- As is a parallelogram, triangle can be slid up to show that the altitudes sum to that of triangle .
Morley's trisector theorem states that, in any triangle, the three points of intersection of the adjacent angle trisectors form an equilateral triangle.
Napoleon's theorem states that, if equilateral triangles are constructed on the sides of any triangle, either all outward, or all inward, the centers of those equilateral triangles themselves form an equilateral triangle.
A version of the isoperimetric inequality for triangles states that the triangle of greatest area among all those with a given perimeter is equilateral.[11]
Viviani's theorem states that, for any interior point in an equilateral triangle with distances , , and from the sides and altitude , independent of the location of .[12]
Pompeiu's theorem states that, if is an arbitrary point in the plane of an equilateral triangle but not on its circumcircle, then there exists a triangle with sides of lengths , , and . That is, , , and satisfy the triangle inequality that the sum of any two of them is greater than the third. If is on the circumcircle then the sum of the two smaller ones equals the longest and the triangle has degenerated into a line, this case is known as Van Schooten's theorem.
Geometric construction
[edit]
An equilateral triangle is easily constructed using a straightedge and compass, because 3 is a Fermat prime. Draw a straight line, and place the point of the compass on one end of the line, and swing an arc from that point to the other point of the line segment. Repeat with the other side of the line. Finally, connect the point where the two arcs intersect with each end of the line segment.
An alternative method is to draw a circle with radius , place the point of the compass on the circle and draw another circle with the same radius. The two circles will intersect in two points. An equilateral triangle can be constructed by taking the two centers of the circles and either of the points of intersection.
In both methods a by-product is the formation of vesica piscis.
The proof that the resulting figure is an equilateral triangle is the first proposition in Book I of Euclid's Elements.

Derivation of area formula
[edit]The area formula in terms of side length can be derived directly using the Pythagorean theorem or using trigonometry.
Using the Pythagorean theorem
[edit]The area of a triangle is half of one side times the height from that side:

The legs of either right triangle formed by an altitude of the equilateral triangle are half of the base , and the hypotenuse is the side of the equilateral triangle. The height of an equilateral triangle can be found using the Pythagorean theorem so that
Substituting into the area formula gives the area formula for the equilateral triangle:
Using trigonometry
[edit]Using trigonometry, the area of a triangle with any two sides and , and an angle between them is
Each angle of an equilateral triangle is 60°, so
The sine of 60° is . Thus since all sides of an equilateral triangle are equal.
Other properties
[edit]An equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center, whose symmetry group is the dihedral group of order 6, . The integer-sided equilateral triangle is the only triangle with integer sides, and three rational angles as measured in degrees.[13] It is the only acute triangle that is similar to its orthic triangle (with vertices at the feet of the altitudes),[14]: p. 19 and the only triangle whose Steiner inellipse is a circle (specifically, the incircle). The triangle of largest area of all those inscribed in a given circle is equilateral, and the triangle of smallest area of all those circumscribed around a given circle is also equilateral.[15] It is the only regular polygon aside from the square that can be inscribed inside any other regular polygon.
By Euler's inequality, the equilateral triangle has the smallest ratio of the circumradius to the inradius of any triangle, with[16]: p.198
Given a point in the interior of an equilateral triangle, the ratio of the sum of its distances from the vertices to the sum of its distances from the sides is greater than or equal to 2, equality holding when is the centroid. In no other triangle is there a point for which this ratio is as small as 2.[17] This is the Erdős–Mordell inequality; a stronger variant of it is Barrow's inequality, which replaces the perpendicular distances to the sides with the distances from to the points where the angle bisectors of , , and cross the sides (, , and being the vertices). There are numerous other triangle inequalities that hold with equality if and only if the triangle is equilateral.
For any point in the plane, with distances , , and from the vertices , , and respectively,[18]
For any point in the plane, with distances , , and from the vertices,[19] where is the circumscribed radius and is the distance between point and the centroid of the equilateral triangle.
For any point on the inscribed circle of an equilateral triangle, with distances , , and from the vertices,[20]
For any point on the minor arc of the circumcircle, with distances , , and from , , and , respectively[12]
Moreover, if point on side divides into segments and with having length and having length , then[12]: 172 which also equals if and which is the optic equation.
For an equilateral triangle:
- The ratio of its area to the area of the incircle, , is the largest of any triangle.[21]: Theorem 4.1
- The ratio of its area to the square of its perimeter, is larger than that of any non-equilateral triangle.[11]
- If a segment splits an equilateral triangle into two regions with equal perimeters and with areas and , then[10]: p.151, #J26
If a triangle is placed in the complex plane with complex vertices , , and , then for either non-real cube root of 1 the triangle is equilateral if and only if[22]: Lemma 2

Notably, the equilateral triangle tiles two dimensional space with six triangles meeting at a vertex, whose dual tessellation is the hexagonal tiling. 3.122, 3.4.6.4, (3.6)2, 32.4.3.4, and 34.6 are all semi-regular tessellations constructed with equilateral triangles.[23]

In three dimensions, equilateral triangles form faces of regular and uniform polyhedra. Three of the five Platonic solids are composed of equilateral triangles: the tetrahedron, octahedron and icosahedron.[24]: p.238 In particular, the tetrahedron, which has four equilateral triangles for faces, can be considered the three-dimensional analogue of the triangle. All Platonic solids can inscribe tetrahedra, as well as be inscribed inside tetrahedra. Equilateral triangles also form uniform antiprisms as well as uniform star antiprisms in three-dimensional space. For antiprisms, two (non-mirrored) parallel copies of regular polygons are connected by alternating bands of equilateral triangles.[25] Specifically for star antiprisms, there are prograde and retrograde (crossed) solutions that join mirrored and non-mirrored parallel star polygons.[26][27] The Platonic octahedron is also a triangular antiprism, which is the first true member of the infinite family of antiprisms (the tetrahedron, as a digonal antiprism, is sometimes considered the first).[24]: p.240
As a generalization, the equilateral triangle belongs to the infinite family of -simplexes, with .[28]
In culture and society
[edit]Equilateral triangles have frequently appeared in man made constructions:
- The shape occurs in modern architecture such as the cross-section of the Gateway Arch.[29]
- Its applications in flags and heraldry includes the flag of Nicaragua[30] and the flag of the Philippines.[31]
- It is a shape of a variety of road signs, including the yield sign.[32]
See also
[edit]References
[edit]- ^ Bencze, Mihály; Wu, Hui-Hua; Wu, Shan-He (2008). "An equivalent form of fundamental triangle inequality and its applications" (PDF). Journal of Inequalities in Pure and Applied Mathematics. 10 (1): 1–6 (Article No. 16). ISSN 1443-5756. MR 2491926. S2CID 115305257. Zbl 1163.26316.
- ^ Dospinescu, G.; Lascu, M.; Pohoata, C.; Letiva, M. (2008). "An elementary proof of Blundon's inequality" (PDF). Journal of Inequalities in Pure and Applied Mathematics. 9 (4): 1-3 (Paper No. 100). ISSN 1443-5756. S2CID 123965364. Zbl 1162.51305.
- ^ Blundon, W. J. (1963). "On Certain Polynomials Associated with the Triangle". Mathematics Magazine. 36 (4). Taylor & Francis: 247–248. doi:10.2307/2687913. JSTOR 2687913. S2CID 124726536. Zbl 0116.12902.
- ^ a b Alsina, Claudi; Nelsen, Roger B. (2009). When less is more. Visualizing basic inequalities. Dolciani Mathematical Expositions. Vol. 36. Washington, D.C.: Mathematical Association of America. pp. 71, 155. doi:10.5948/upo9781614442028. ISBN 978-0-88385-342-9. MR 2498836. OCLC 775429168. S2CID 117769827. Zbl 1163.00008.
- ^ a b Pohoata, Cosmin (2010). "A new proof of Euler's inradius - circumradius inequality" (PDF). Gazeta Matematica Seria B (3): 121–123. S2CID 124244932.
- ^ a b c Andreescu, Titu; Andrica, Dorian (2006). Complex Numbers from A to...Z (1st ed.). Boston, MA: Birkhäuser. pp. 70, 113–115. doi:10.1007/0-8176-4449-0. ISBN 978-0-8176-4449-9. OCLC 871539199. S2CID 118951675.
- ^ Owen, Byer; Felix, Lazebnik; Deirdre, Smeltzer (2010). Methods for Euclidean Geometry. Classroom Resource Materials. Vol. 37. Washington, D.C.: Mathematical Association of America. pp. 36, 39. doi:10.5860/choice.48-3331. ISBN 9780883857632. OCLC 501976971. S2CID 118179744.
- ^ Yiu, Paul (1998). "Notes on Euclidean Geometry" (PDF). Florida Atlantic University, Department of Mathematical Sciences (Course Notes).
- ^ a b Cerin, Zvonko (2004). "The vertex-midpoint-centroid triangles" (PDF). Forum Geometricorum. 4: 97–109.
- ^ a b "Inequalities proposed in "Crux Mathematicorum"" (PDF).
- ^ a b Chakerian, G. D. "A Distorted View of Geometry." Ch. 7 in Mathematical Plums (R. Honsberger, editor). Washington, DC: Mathematical Association of America, 1979: 147.
- ^ a b c Posamentier, Alfred S.; Salkind, Charles T. (1996). Challenging Problems in Geometry. Dover Publ.
- ^ Conway, J. H., and Guy, R. K., "The only rational triangle", in The Book of Numbers, 1996, Springer-Verlag, pp. 201 and 228–239.
- ^ Leon Bankoff and Jack Garfunkel, "The heptagonal triangle", Mathematics Magazine 46 (1), January 1973, 7–19,
- ^ Dörrie, Heinrich (1965). 100 Great Problems of Elementary Mathematics. Dover Publ. pp. 379–380.
- ^ Svrtan, Dragutin; Veljan, Darko (2012). "Non-Euclidean versions of some classical triangle inequalities" (PDF). Forum Geometricorum. 12: 197–209.
- ^ Lee, Hojoo (2001). "Another proof of the Erdős–Mordell Theorem" (PDF). Forum Geometricorum. 1: 7–8.
- ^ Gardner, Martin, "Elegant Triangles", in the book Mathematical Circus, 1979, p. 65.
- ^ Meskhishvili, Mamuka (2021). "Cyclic Averages of Regular Polygonal Distances" (PDF). International Journal of Geometry. 10: 58–65.
- ^ De, Prithwijit (2008). "Curious properties of the circumcircle and incircle of an equilateral triangle" (PDF). Mathematical Spectrum. 41 (1): 32–35.
- ^ Minda, D.; Phelps, S. (2008). "Triangles, ellipses, and cubic polynomials". American Mathematical Monthly. 115 (October): 679–689. doi:10.1080/00029890.2008.11920581. JSTOR 27642581. S2CID 15049234.
- ^ Dao, Thanh Oai (2015). "Equilateral triangles and Kiepert perspectors in complex numbers" (PDF). Forum Geometricorum. 15: 105–114.
- ^ Grünbaum, Branko; Shepard, Geoffrey (November 1977). "Tilings by Regular Polygons" (PDF). Mathematics Magazine. 50 (5). Taylor & Francis, Ltd.: 231–234. doi:10.2307/2689529. JSTOR 2689529. MR 1567647. S2CID 123776612. Zbl 0385.51006.
- ^ a b Johnson, Norman W. (2018). Geometries and Transformations (1st ed.). Cambridge: Cambridge University Press. pp. xv, 1–438. doi:10.1017/9781316216477. ISBN 978-1107103405. S2CID 125948074. Zbl 1396.51001.
- ^ Cromwell, Peter T. (1997). "Chapter 2: The Archimedean solids". Polyhedra (1st ed.). New York: Cambridge University Press. p. 85. ISBN 978-0521664059. MR 1458063. OCLC 41212721. Zbl 0888.52012.
- ^ Klitzing, Richard. "n-antiprism with winding number d". Polytopes & their Incidence Matrices. bendwavy.org (Anton Sherwood). Retrieved 2023-03-09.
- ^ Webb, Robert. "Stella Polyhedral Glossary". Stella. Retrieved 2023-03-09.
- ^ H. S. M. Coxeter (1948). Regular Polytopes (1 ed.). London: Methuen & Co. LTD. pp. 120–121. OCLC 4766401. Zbl 0031.06502.
- ^ Pelkonen, Eeva-Liisa; Albrecht, Donald, eds. (2006). Eero Saarinen: Shaping the Future. Yale University Press. pp. 160, 224, 226. ISBN 978-0972488129.
- ^ White, Steven F.; Calderón, Esthela (2008). Culture and Customs of Nicaragua. Greenwood Press. p. 3. ISBN 978-0313339943.
- ^ Guillermo, Artemio R. (2012). Historical Dictionary of the Philippines. Scarecrow Press. p. 161. ISBN 978-0810872462.
- ^ Riley, Michael W.; Cochran, David J.; Ballard, John L. (December 1982). "An Investigation of Preferred Shapes for Warning Labels". Human Factors: The Journal of the Human Factors and Ergonomics Society. 24 (6): 737–742. doi:10.1177/001872088202400610. S2CID 109362577.
External links
[edit]| Triangles | |||||||
|---|---|---|---|---|---|---|---|
| Quadrilaterals | |||||||
| By number of sides |
| ||||||
| Star polygons | |||||||
| Classes | |||||||























































































![{\displaystyle p^{4}+q^{4}+t^{4}=3\left[\left(R^{2}+L^{2}\right)^{2}+2R^{2}L^{2}\right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9b9926a561be54775a0fa6d3c7fc03ccf00c2378)
























