| Regular decagram | |
|---|---|
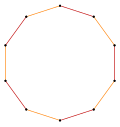
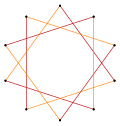
 A regular decagram | |
| Type | Regular star polygon |
| Edges and vertices | 10 |
| Schläfli symbol | {10/3} t{5/3} |
| Coxeter–Dynkin diagrams | |
| Symmetry group | Dihedral (D10) |
| Internal angle (degrees) | 72° |
| Properties | star, cyclic, equilateral, isogonal, isotoxal |
| Dual polygon | self |
| Star polygons |
|---|
|
|

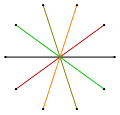
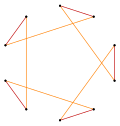
In geometry, a decagram is a 10-point star polygon. There is one regular decagram, containing the vertices of a regular decagon, but connected by every third point. Its Schläfli symbol is {10/3}.[1]
The name decagram combines a numeral prefix, deca-, with the Greek suffix -gram. The -gram suffix derives from γραμμῆς (grammēs) meaning a line.[2]