Star polygon with 12 vertices
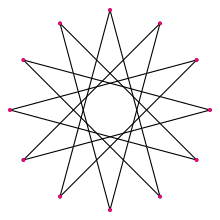
In geometry, a dodecagram (from Greek δώδεκα (dṓdeka) 'twelve', and γραμμῆς (grammēs) 'line'[1]) is a star polygon or compound with 12 vertices. There is one regular dodecagram polygon (with Schläfli symbol {12/5} and a turning number of 5). There are also 4 regular compounds {12/2}, {12/3}, {12/4}, and {12/6}.
Regular dodecagram
There is one regular form: {12/5}, containing 12 vertices, with a turning number of 5. A regular dodecagram has the same vertex arrangement as a regular dodecagon, which may be regarded as {12/1}.
Dodecagrams as regular compounds
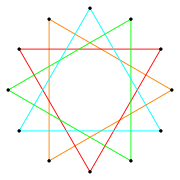
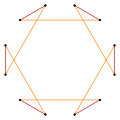
There are four regular dodecagram star figures: {12/2}=2{6}, {12/3}=3{4}, {12/4}=4{3}, and {12/6}=6{2}. The first is a compound of two hexagons, the second is a compound of three squares, the third is a compound of four triangles, and the fourth is a compound of six straight-sided digons. The last two can be considered compounds of two compound hexagrams and the last as three compound tetragrams.
Complete graph
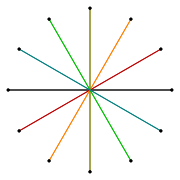
Superimposing all the dodecagons and dodecagrams on each other – including the degenerate compound of six digons (line segments), {12/6} – produces the complete graph K12.
K12

|
black: the twelve corner points (nodes)
red: {12} regular dodecagon
green: {12/2}=2{6} two hexagons
blue: {12/3}=3{4} three squares
cyan: {12/4}=4{3} four triangles
magenta: {12/5} regular dodecagram
yellow: {12/6}=6{2} six digons
|
Regular dodecagrams in polyhedra
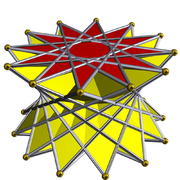
Dodecagrams can also be incorporated into uniform polyhedra. Below are the three prismatic uniform polyhedra containing regular dodecagrams (there are no other dodecagram-containing uniform polyhedra).
Dodecagrams can also be incorporated into star tessellations of the Euclidean plane.