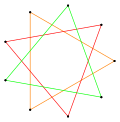
Enneagram
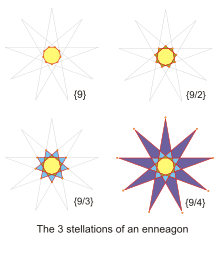Enneagrams shown as sequential stellations
Edges and vertices	9
Symmetry group	Dihedral (D9)
Internal angle (degrees)	100° {9/2} 20° {9/4}

In geometry, an enneagram (🟙 U+1F7D9) is a nine-pointed plane figure. It is sometimes called a nonagram, nonangle, or enneagon.^[1]

The word 'enneagram' combines the numeral prefix ennea- with the Greek suffix -gram. The gram suffix derives from γραμμῆ (grammē) meaning a line.^[2]

Regular enneagram

A regular enneagram is a 9-sided star polygon. It is constructed using the same points as the regular enneagon, but the points are connected in fixed steps. Two forms of regular enneagram exist:

• One form connects every second point and is represented by the Schläfli symbol {9/2}.
• The other form connects every fourth point and is represented by the Schläfli symbol {9/4}.

There is also a star figure, {9/3} or 3{3}, made from the regular enneagon points but connected as a compound of three equilateral triangles.^[3][4] (If the triangles are alternately interlaced, this results in a Brunnian link.) This star figure is sometimes known as the star of Goliath, after {6/2} or 2{3}, the star of David.^[5]

Compound	Regular star	Regular compound	Regular star
Complete graph K9	{9/2}	{9/3} or 3{3}	{9/4}

Other enneagram figures

The final stellation of the icosahedron has 2-isogonal enneagram faces. It is a 9/4 wound star polyhedron, but the vertices are not equally spaced.

The Fourth Way teachings and the Enneagram of Personality use an irregular enneagram consisting of an equilateral triangle and an irregular hexagram based on 142857.

The Bahá'í nine-pointed star

A 9/3 enneagram

The nine-pointed star or enneagram can also symbolize the nine gifts or fruits of the Holy Spirit.^[6]

In popular culture

• The heavy metal band Slipknot previously used the {9/3} star figure enneagram^[7] and currently uses the {9/4} polygon as a symbol. The prior figure can be seen on the cover of All Hope Is Gone.