| Disdyakis triacontahedron | |
|---|---|
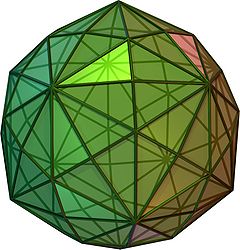 Click on picture for large version | |
| Type | Catalan |
| Coxeter diagram | |
| Face polygon | scalene triangle |
| Faces | 120 |
| Edges | 180 |
| Vertices | 62 = 12 + 20 + 30 |
| Face configuration | V4.6.10 |
| Symmetry group | Ih, H3, [5,3], (*532) |
| Rotation group | I, [5,3]+, (532) |
| Dihedral angle | 164° 53' 17" |
| Dual polyhedron | truncated icosidodecahedron |
| Properties | convex, face-transitive |
 Net | |
In geometry, a disdyakis triacontahedron, or hexakis icosahedron is a Catalan solid with 120 faces and the dual to the Archimedean truncated icosidodecahedron. As such it is face uniform but with irregular face polygons. It looks a bit like an inflated rhombic triacontahedron—if one replaces each face of the rhombic triacontahedron with a single vertex and four triangles in a regular fashion one ends up with a disdyakis triacontahedron. That is, the disdyakis triacontahedron is the Kleetope of the rhombic triacontahedron. It also has the most faces among the Archimedean and Catalan solids, with the snub dodecahedron, with 92 faces, in second place.
The edges of the polyhedron projected onto a sphere form great circles, and represent all ten mirror planes of reflective Ih icosahedral symmetry, as shown in this image. Combining pairs of light and dark triangles define the fundamental domains of the nonreflective I icosahedral symmetry.

|

|