| Part of a series on |
| Astrodynamics |
|---|
The orbital period (also revolution period) is the amount of time a given astronomical object takes to complete one orbit around another object. In astronomy, it usually applies to planets or asteroids orbiting the Sun, moons orbiting planets, exoplanets orbiting other stars, or binary stars. It may also refer to the time it takes a satellite orbiting a planet or moon to complete one orbit.
For celestial objects in general, the orbital period is determined by a 360° revolution of one body around its primary, e.g. Earth around the Sun.
Periods in astronomy are expressed in units of time, usually hours, days, or years.
Small body orbiting a central body
[edit]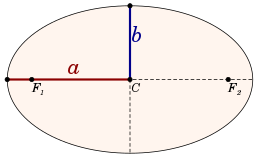
According to Kepler's Third Law, the orbital period T of two point masses orbiting each other in a circular or elliptic orbit is:[1]
where:
- a is the orbit's semi-major axis
- G is the gravitational constant,
- M is the mass of the more massive body.
For all ellipses with a given semi-major axis the orbital period is the same, regardless of eccentricity.
Inversely, for calculating the distance where a body has to orbit in order to have a given orbital period T:
For instance, for completing an orbit every 24 hours around a mass of 100 kg, a small body has to orbit at a distance of 1.08 meters from the central body's center of mass.
In the special case of perfectly circular orbits, the semimajor axis a is equal to the radius of the orbit, and the orbital velocity is constant and equal to
where:
- r is the circular orbit's radius in meters,
This corresponds to 1⁄√2 times (≈ 0.707 times) the escape velocity.
Effect of central body's density
[edit]For a perfect sphere of uniform density, it is possible to rewrite the first equation without measuring the mass as:
where:
- r is the sphere's radius
- a is the orbit's semi-major axis in metres,
- G is the gravitational constant,
- ρ is the density of the sphere in kilograms per cubic metre.
For instance, a small body in circular orbit 10.5 cm above the surface of a sphere of tungsten half a metre in radius would travel at slightly more than 1 mm/s, completing an orbit every hour. If the same sphere were made of lead the small body would need to orbit just 6.7 mm above the surface for sustaining the same orbital period.
When a very small body is in a circular orbit barely above the surface of a sphere of any radius and mean density ρ (in kg/m3), the above equation simplifies to (since M = Vρ = 4/3πa3ρ)
Thus the orbital period in low orbit depends only on the density of the central body, regardless of its size.
So, for the Earth as the central body (or any other spherically symmetric body with the same mean density, about 5,515 kg/m3,[2] e.g. Mercury with 5,427 kg/m3 and Venus with 5,243 kg/m3) we get:
- T = 1.41 hours
and for a body made of water (ρ ≈ 1,000 kg/m3),[3] or bodies with a similar density, e.g. Saturn's moons Iapetus with 1,088 kg/m3 and Tethys with 984 kg/m3 we get:
- T = 3.30 hours
Thus, as an alternative for using a very small number like G, the strength of universal gravity can be described using some reference material, such as water: the orbital period for an orbit just above the surface of a spherical body of water is 3 hours and 18 minutes. Conversely, this can be used as a kind of "universal" unit of time if we have a unit of density.
Two bodies orbiting each other
[edit]
In celestial mechanics, when both orbiting bodies' masses have to be taken into account, the orbital period T can be calculated as follows:[4]
where:
- a is the sum of the semi-major axes of the ellipses in which the centers of the bodies move, or equivalently, the semi-major axis of the ellipse in which one body moves, in the frame of reference with the other body at the origin (which is equal to their constant separation for circular orbits),
- M1 + M2 is the sum of the masses of the two bodies,
- G is the gravitational constant.
In a parabolic or hyperbolic trajectory, the motion is not periodic, and the duration of the full trajectory is infinite.
Related periods
[edit]For celestial objects in general, the orbital period typically refers to the sidereal period, determined by a 360° revolution of one body around its primary relative to the fixed stars projected in the sky. For the case of the Earth orbiting around the Sun, this period is referred to as the sidereal year. This is the orbital period in an inertial (non-rotating) frame of reference.
Orbital periods can be defined in several ways. The tropical period is more particularly about the position of the parent star. It is the basis for the solar year, and respectively the calendar year.
The synodic period refers not to the orbital relation to the parent star, but to other celestial objects, making it not a merely different approach to the orbit of an object around its parent, but a period of orbital relations with other objects, normally Earth, and their orbits around the Sun. It applies to the elapsed time where planets return to the same kind of phenomenon or location, such as when any planet returns between its consecutive observed conjunctions with or oppositions to the Sun. For example, Jupiter has a synodic period of 398.8 days from Earth; thus, Jupiter's opposition occurs once roughly every 13 months.
There are many periods related to the orbits of objects, each of which are often used in the various fields of astronomy and astrophysics, particularly they must not be confused with other revolving periods like rotational periods. Examples of some of the common orbital ones include the following:
- The synodic period is the amount of time that it takes for an object to reappear at the same point in relation to two or more other objects. In common usage, these two objects are typically Earth and the Sun. The time between two successive oppositions or two successive conjunctions is also equal to the synodic period. For celestial bodies in the solar system, the synodic period (with respect to Earth and the Sun) differs from the tropical period owing to Earth's motion around the Sun. For example, the synodic period of the Moon's orbit as seen from Earth, relative to the Sun, is 29.5 mean solar days, since the Moon's phase and position relative to the Sun and Earth repeats after this period. This is longer than the sidereal period of its orbit around Earth, which is 27.3 mean solar days, owing to the motion of Earth around the Sun.
- The draconitic period (also draconic period or nodal period), is the time that elapses between two passages of the object through its ascending node, the point of its orbit where it crosses the ecliptic from the southern to the northern hemisphere. This period differs from the sidereal period because both the orbital plane of the object and the plane of the ecliptic precess with respect to the fixed stars, so their intersection, the line of nodes, also precesses with respect to the fixed stars. Although the plane of the ecliptic is often held fixed at the position it occupied at a specific epoch, the orbital plane of the object still precesses, causing the draconitic period to differ from the sidereal period.[5]
- The anomalistic period is the time that elapses between two passages of an object at its periapsis (in the case of the planets in the Solar System, called the perihelion), the point of its closest approach to the attracting body. It differs from the sidereal period because the object's semi-major axis typically advances slowly.
- Also, the tropical period of Earth (a tropical year) is the interval between two alignments of its rotational axis with the Sun, also viewed as two passages of the object at a right ascension of 0 hr. One Earth year is slightly shorter than the period for the Sun to complete one circuit along the ecliptic (a sidereal year) because the inclined axis and equatorial plane slowly precess (rotate with respect to reference stars), realigning with the Sun before the orbit completes. This cycle of axial precession for Earth, known as precession of the equinoxes, recurs roughly every 25,772 years.[6]
Periods can be also defined under different specific astronomical definitions that are mostly caused by the small complex external gravitational influences of other celestial objects. Such variations also include the true placement of the centre of gravity between two astronomical bodies (barycenter), perturbations by other planets or bodies, orbital resonance, general relativity, etc. Most are investigated by detailed complex astronomical theories using celestial mechanics using precise positional observations of celestial objects via astrometry.
Synodic period
[edit]One of the observable characteristics of two bodies which orbit a third body in different orbits, and thus have different orbital periods, is their synodic period, which is the time between conjunctions.
An example of this related period description is the repeated cycles for celestial bodies as observed from the Earth's surface, the synodic period, applying to the elapsed time where planets return to the same kind of phenomenon or location — for example, when any planet returns between its consecutive observed conjunctions with or oppositions to the Sun. For example, Jupiter has a synodic period of 398.8 days from Earth; thus, Jupiter's opposition occurs once roughly every 13 months.
If the orbital periods of the two bodies around the third are called T1 and T2, so that T1 < T2, their synodic period is given by:[7]
Examples of sidereal and synodic periods
[edit]Table of synodic periods in the Solar System, relative to Earth:[citation needed]
| Object | Sidereal period | Synodic period | ||
|---|---|---|---|---|
| (yr) | (d) | (yr) | (d)[8] | |
| Mercury | 0.240846 | 87.9691 days | 0.317 | 115.88 |
| Venus | 0.615 | 224.7 days[9] | 1.599 | 583.9 |
| Earth | 1 | 365.25636 solar days | — | |
| Mars | 1.881 | 687.0[9] | 2.135 | 779.9 |
| Jupiter | 11.86 | 4331[9] | 1.092 | 398.9 |
| Saturn | 29.46 | 10,747[9] | 1.035 | 378.1 |
| Uranus | 84.01 | 30,589[9] | 1.012 | 369.7 |
| Neptune | 164.8 | 59,800[9] | 1.006 | 367.5 |
| 134340 Pluto | 248.1 | 90,560[9] | 1.004 | 366.7 |
| Moon | 0.0748 | 27.32 days | 0.0809 | 29.5306 |
| 99942 Apophis (near-Earth asteroid) | 0.886 | 7.769 | 2,837.6 | |
| 4 Vesta | 3.629 | 1.380 | 504.0 | |
| 1 Ceres | 4.600 | 1.278 | 466.7 | |
| 10 Hygiea | 5.557 | 1.219 | 445.4 | |
| 2060 Chiron | 50.42 | 1.020 | 372.6 | |
| 50000 Quaoar | 287.5 | 1.003 | 366.5 | |
| 136199 Eris | 557 | 1.002 | 365.9 | |
| 90377 Sedna | 12050 | 1.0001 | 365.3 [citation needed] | |
In the case of a planet's moon, the synodic period usually means the Sun-synodic period, namely, the time it takes the moon to complete its illumination phases, completing the solar phases for an astronomer on the planet's surface. The Earth's motion does not determine this value for other planets because an Earth observer is not orbited by the moons in question. For example, Deimos's synodic period is 1.2648 days, 0.18% longer than Deimos's sidereal period of 1.2624 d.[citation needed]
Synodic periods relative to other planets
[edit]The concept of synodic period applies not just to the Earth, but also to other planets as well, and the formula for computation is the same as the one given above. Here is a table which lists the synodic periods of some planets relative to each other:
| Relative to | Mars | Jupiter | Saturn | Chiron | Uranus | Neptune | Pluto | Quaoar | Eris |
|---|---|---|---|---|---|---|---|---|---|
| Sun | 1.881 | 11.86 | 29.46 | 50.42 | 84.01 | 164.8 | 248.1 | 287.5 | 557.0 |
| Mars | 2.236 | 2.009 | 1.954 | 1.924 | 1.903 | 1.895 | 1.893 | 1.887 | |
| Jupiter | 19.85 | 15.51 | 13.81 | 12.78 | 12.46 | 12.37 | 12.12 | ||
| Saturn | 70.87 | 45.37 | 35.87 | 33.43 | 32.82 | 31.11 | |||
| 2060 Chiron | 126.1 | 72.65 | 63.28 | 61.14 | 55.44 | ||||
| Uranus | 171.4 | 127.0 | 118.7 | 98.93 | |||||
| Neptune | 490.8 | 386.1 | 234.0 | ||||||
| Pluto | 1810.4 | 447.4 | |||||||
| 50000 Quaoar | 594.2 |
Example of orbital periods: binary stars
[edit]| Binary star | Orbital period. |
|---|---|
| AM Canum Venaticorum | 17.146 minutes |
| Beta Lyrae AB | 12.9075 days |
| Alpha Centauri AB | 79.91 years |
| Proxima Centauri – Alpha Centauri AB | 500,000 years or more |
See also
[edit]- Geosynchronous orbit derivation
- Rotation period – time that it takes to complete one revolution around its axis of rotation
- Satellite revisit period
- Sidereal time
- Sidereal year
- Opposition (astronomy)
- List of periodic comets
- Leap year
Notes
[edit]- ^ Bate, Mueller & White (1971), p. 33.
- ^ Density of the Earth, wolframalpha.com
- ^ Density of water, wolframalpha.com
- ^ Bradley W. Carroll, Dale A. Ostlie. An introduction to modern astrophysics. 2nd edition. Pearson 2007, p. 49 (equation 2.37 simplified).
- ^ Oliver Montenbruck, Eberhard Gill (2000). Satellite Orbits: Models, Methods, and Applications. Springer Science & Business Media. p. 50. ISBN 978-3-540-67280-7.
- ^ "Precession of the Earth's Axis - Wolfram Demonstrations Project". demonstrations.wolfram.com. Retrieved 2019-02-10.
- ^ Hannu Karttunen; et al. (2016). Fundamental Astronomy (6th ed.). Springer. p. 145. ISBN 9783662530450. Retrieved December 7, 2018.
- ^ "Questions and Answers - Sten's Space Blog". www.astronomycafe.net.
- ^ a b c d e f g "Planetary Fact Sheet". nssdc.gsfc.nasa.gov.
Bibliography
[edit]- Bate, Roger B.; Mueller, Donald D.; White, Jerry E. (1971), Fundamentals of Astrodynamics, Dover
External links
[edit]Gravitational orbits | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Types |
| ||||||||
| Parameters |
| ||||||||
| Maneuvers | |||||||||
| Orbital mechanics |
| ||||||||

![{\displaystyle a={\sqrt[{3}]{\frac {GMT^{2)){4\pi ^{2))))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/acc0794d19344d83b82ba93518c68a0fccd0b31b)




