| Part of a series on |
| Economics |
|---|
In welfare economics, a Pareto improvement formalizes the idea of an outcome being "better in every possible way". A change is called a Pareto improvement if it leaves everyone in a society better-off (or at least as well-off as they were before). A situation is called Pareto efficient or Pareto optimal if all possible Pareto improvements have already been made; in other words, there are no longer any ways left to make one person better-off, unless we are willing to make some other person worse-off.[1]
In social choice theory, the same concept is sometimes called the unanimity principle, which says that if everyone in a society (non-strictly) prefers A to B, society as a whole also non-strictly prefers A to B.
The Pareto front consists of all Pareto-efficient situations.[2]
In addition to the context of efficiency in allocation, the concept of Pareto efficiency also arises in the context of efficiency in production vs. x-inefficiency: a set of outputs of goods is Pareto-efficient if there is no feasible re-allocation of productive inputs such that output of one product increases while the outputs of all other goods either increase or remain the same.[3]
Besides economics, the notion of Pareto efficiency has also been applied to selecting alternatives in engineering and biology. Each option is first assessed, under multiple criteria, and then a subset of options is identified with the property that no other option can categorically outperform the specified option. It is a statement of impossibility of improving one variable without harming other variables in the subject of multi-objective optimization (also termed Pareto optimization).
History
[edit]The concept is named after Vilfredo Pareto (1848–1923), an Italian civil engineer and economist, who used the concept in his studies of economic efficiency and income distribution.
Pareto originally used the word "optimal" for the concept, but this is somewhat of a misnomer: Pareto's concept more closely aligns with an idea of "efficiency", because it does not identify a single "best" (optimal) outcome. Instead, it only identifies a set of outcomes that might be considered optimal, by at least one person.[4]
Overview
[edit]Formally, a state is Pareto-optimal if there is no alternative state where at least one participant's well-being is higher, and nobody else's well-being is lower. If there is a state change that satisfies this condition, the new state is called a "Pareto improvement". When no Pareto improvements are possible, the state is a "Pareto optimum".
In other words, Pareto efficiency is when it is impossible to make one party better off without making another party worse off. [5] This state indicates that resources can no longer be allocated in a way that makes one party better off without harming other parties. In a state of Pareto Efficiency, resources are allocated in the most efficient way possible. [5]
Pareto efficiency is mathematically represented when there is no other strategy profile s' such that ui (s') ≥ ui (s) for every player i and uj (s') > uj (s) for some player j. In this equation s represents the strategy profile, u represents the utility or benefit, and j represents the player.[6]
Efficiency is an important criterion for judging behavior in a game. In a notable and often analyzed game known as Prisoner's Dilemma, depicted below as a normal-form game, this concept of efficiency can be observed, in that the strategy profile (Cooperate, Cooperate) is more efficient than (Defect, Defect).[6]
| Cooperate | Defect | |
|---|---|---|
| Cooperate | 1, 1 | 0, 3 |
| Defect | 3, 0 | 2, 2 |
Using the definition listed above, u(Ci) ≥ u(Di) for i ∈ {1, 2}, thus yielding this strategy as a Pareto efficient strategy. In other words, both players receive an increase in payoff by selecting Cooperate over Defect.
In zero-sum games, every outcome is Pareto-efficient.
A special case of a state is an allocation of resources. The formal presentation of the concept in an economy is the following: Consider an economy with agents and goods. Then an allocation , where for all i, is Pareto-optimal if there is no other feasible allocation where, for utility function for each agent , for all with for some .[7] Here, in this simple economy, "feasibility" refers to an allocation where the total amount of each good that is allocated sums to no more than the total amount of the good in the economy. In a more complex economy with production, an allocation would consist both of consumption vectors and production vectors, and feasibility would require that the total amount of each consumed good is no greater than the initial endowment plus the amount produced.
Under the assumptions of the first welfare theorem, a competitive market leads to a Pareto-efficient outcome. This result was first demonstrated mathematically by economists Kenneth Arrow and Gérard Debreu.[8] However, the result only holds under the assumptions of the theorem: markets exist for all possible goods, there are no externalities, markets are perfectly competitive, and market participants have perfect information.
In the absence of perfect information or complete markets, outcomes will generally be Pareto-inefficient, per the Greenwald–Stiglitz theorem.[9]
The second welfare theorem is essentially the reverse of the first welfare theorem. It states that under similar, ideal assumptions, any Pareto optimum can be obtained by some competitive equilibrium, or free market system, although it may also require a lump-sum transfer of wealth.[7]
Pareto efficiency and market failure
[edit]An ineffective distribution of resources in a free market is known as market failure. Given that there is room for improvement, market failure implies Pareto inefficiency.
For instance, excessive use of negative commodities (such as drugs and cigarettes) results in expenses to non-smokers as well as early mortality for smokers. Cigarette taxes may help individuals stop smoking while also raising money to address ailments brought on by smoking.
Pareto efficiency and equity
[edit]A Pareto improvement may be seen, but this does not always imply that the result is desirable or equitable. After a Pareto improvement, inequality could still exist. However, it does imply that any change will violate the "do no harm" principle, because at least one person will be worse off.
A society may be Pareto efficient but have significant levels of inequality. The most equitable course of action would be to split the pie into three equal portions if there were three persons and a pie. The third person does not lose out (even if he does not partake in the pie), hence splitting it in half and giving it to two individuals would be considered Pareto efficient.
On a frontier of production possibilities, Pareto efficiency will happen. It is impossible to raise the output of products without decreasing the output of services when an economy is functioning on a basic production potential frontier, such as at point A, B, or C.
Pareto order
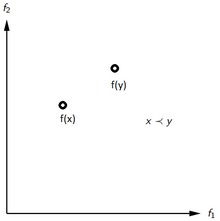
[edit]If multiple sub-goals (with ) exist, combined into a vector-valued objective function , generally, finding a unique optimum becomes challenging. This is due to the absence of a total order relation for . In this case, various solutions can be "incomparable"[10] as there is no total order relation to facilitate the comparison . Only the Pareto order is applicable:
Consider a vector-valued minimization problem: Pareto dominates if and only if:[11] : and We then write , where is the Pareto order. This means that is not worse than in any goal but is better (since smaller) in at least one goal . The Pareto order is a strict partial order, though it is not a product order (neither non-strict nor strict).
If[11] , then this defines a preorder in the search space and we say Pareto dominates the alternative and we write .

Variants
[edit]Weak Pareto efficiency
[edit]Weak Pareto efficiency is a situation that cannot be strictly improved for every individual.[12]
Formally, a strong Pareto improvement is defined as a situation in which all agents are strictly better-off (in contrast to just "Pareto improvement", which requires that one agent is strictly better-off and the other agents are at least as good). A situation is weak Pareto-efficient if it has no strong Pareto improvements.
Any strong Pareto improvement is also a weak Pareto improvement. The opposite is not true; for example, consider a resource allocation problem with two resources, which Alice values at {10, 0}, and George values at {5, 5}. Consider the allocation giving all resources to Alice, where the utility profile is (10, 0):
- It is a weak PO, since no other allocation is strictly better to both agents (there are no strong Pareto improvements).
- But it is not a strong PO, since the allocation in which George gets the second resource is strictly better for George and weakly better for Alice (it is a weak Pareto improvement) – its utility profile is (10, 5).
A market does not require local nonsatiation to get to a weak Pareto optimum.[13]
Constrained Pareto efficiency
[edit]Constrained Pareto efficiency is a weakening of Pareto optimality, accounting for the fact that a potential planner (e.g., the government) may not be able to improve upon a decentralized market outcome, even if that outcome is inefficient. This will occur if it is limited by the same informational or institutional constraints as are individual agents.[14]
An example is of a setting where individuals have private information (for example, a labor market where the worker's own productivity is known to the worker but not to a potential employer, or a used-car market where the quality of a car is known to the seller but not to the buyer) which results in moral hazard or an adverse selection and a sub-optimal outcome. In such a case, a planner who wishes to improve the situation is unlikely to have access to any information that the participants in the markets do not have. Hence, the planner cannot implement allocation rules which are based on the idiosyncratic characteristics of individuals; for example, "if a person is of type A, they pay price p1, but if of type B, they pay price p2" (see Lindahl prices). Essentially, only anonymous rules are allowed (of the sort "Everyone pays price p") or rules based on observable behavior; "if any person chooses x at price px, then they get a subsidy of ten dollars, and nothing otherwise". If there exists no allowed rule that can successfully improve upon the market outcome, then that outcome is said to be "constrained Pareto-optimal".
Fractional Pareto efficiency
[edit]Fractional Pareto efficiency is a strengthening of Pareto efficiency in the context of fair item allocation. An allocation of indivisible items is fractionally Pareto-efficient (fPE or fPO) if it is not Pareto-dominated even by an allocation in which some items are split between agents. This is in contrast to standard Pareto efficiency, which only considers domination by feasible (discrete) allocations.[15][16]
As an example, consider an item allocation problem with two items, which Alice values at {3, 2} and George values at {4, 1}. Consider the allocation giving the first item to Alice and the second to George, where the utility profile is (3, 1):
- It is Pareto-efficient, since any other discrete allocation (without splitting items) makes someone worse-off.
- However, it is not fractionally Pareto-efficient, since it is Pareto-dominated by the allocation giving to Alice 1/2 of the first item and the whole second item, and the other 1/2 of the first item to George – its utility profile is (3.5, 2).
Ex-ante Pareto efficiency
[edit]When the decision process is random, such as in fair random assignment or random social choice or fractional approval voting, there is a difference between ex-post and ex-ante Pareto efficiency:
- Ex-post Pareto efficiency means that any outcome of the random process is Pareto-efficient.
- Ex-ante Pareto efficiency means that the lottery determined by the process is Pareto-efficient with respect to the expected utilities. That is: no other lottery gives a higher expected utility to one agent and at least as high expected utility to all agents.
If some lottery L is ex-ante PE, then it is also ex-post PE. Proof: suppose that one of the ex-post outcomes x of L is Pareto-dominated by some other outcome y. Then, by moving some probability mass from x to y, one attains another lottery L' that ex-ante Pareto-dominates L.
The opposite is not true: ex-ante PE is stronger that ex-post PE. For example, suppose there are two objects – a car and a house. Alice values the car at 2 and the house at 3; George values the car at 2 and the house at 9. Consider the following two lotteries:
- With probability 1/2, give car to Alice and house to George; otherwise, give car to George and house to Alice. The expected utility is (2/2 + 3/2) = 2.5 for Alice and (2/2 + 9/2) = 5.5 for George. Both allocations are ex-post PE, since the one who got the car cannot be made better-off without harming the one who got the house.
- With probability 1, give car to Alice, then with probability 1/3 give the house to Alice, otherwise give it to George. The expected utility is (2 + 3/3) = 3 for Alice and (9 × 2/3) = 6 for George. Again, both allocations are ex-post PE.
While both lotteries are ex-post PE, the lottery 1 is not ex-ante PE, since it is Pareto-dominated by lottery 2.
Another example involves dichotomous preferences.[17] There are 5 possible outcomes (a, b, c, d, e) and 6 voters. The voters' approval sets are (ac, ad, ae, bc, bd, be). All five outcomes are PE, so every lottery is ex-post PE. But the lottery selecting c, d, e with probability 1/3 each is not ex-ante PE, since it gives an expected utility of 1/3 to each voter, while the lottery selecting a, b with probability 1/2 each gives an expected utility of 1/2 to each voter.
Bayesian Pareto efficiency
[edit]Bayesian efficiency is an adaptation of Pareto efficiency to settings in which players have incomplete information regarding the types of other players.
Ordinal Pareto efficiency
[edit]Ordinal Pareto efficiency is an adaptation of Pareto efficiency to settings in which players report only rankings on individual items, and we do not know for sure how they rank entire bundles.
Pareto efficiency and equity
[edit]Although an outcome may be a Pareto improvement, this does not imply that the outcome is equitable. It is possible that inequality persists even after a Pareto improvement. Despite the fact that it is frequently used in conjunction with the idea of Pareto optimality, the term "efficiency" refers to the process of increasing societal productivity.[18] It is possible for a society to have Pareto efficiency while also have high levels of inequality. Consider the following scenario: there is a pie and three persons; the most equitable way would be to divide the pie into three equal portions. However, if the pie is divided in half and shared between two people, it is considered Pareto efficient – meaning that the third person does not lose out (despite the fact that he does not receive a piece of the pie). When making judgments, it is critical to consider a variety of aspects, including social efficiency, overall welfare, and issues such as diminishing marginal value.
Pareto efficiency and market failure
[edit]In order to fully understand market failure, one must first comprehend market success, which is defined as the ability of a set of idealized competitive markets to achieve an equilibrium allocation of resources that is Pareto-optimal in terms of resource allocation. According to the definition of market failure, it is a circumstance in which the conclusion of the first fundamental theorem of welfare is erroneous; that is, when the allocations made through markets are not efficient.[19] In a free market, market failure is defined as an inefficient allocation of resources. Due to the fact that it is feasible to improve, market failure implies Pareto inefficiency. For example, excessive consumption of depreciating items (drugs/tobacco) results in external costs to non-smokers, as well as premature death for smokers who do not quit. An increase in the price of cigarettes could motivate people to quit smoking while also raising funds for the treatment of smoking-related ailments.
Approximate Pareto efficiency
[edit]Given some ε > 0, an outcome is called ε-Pareto-efficient if no other outcome gives all agents at least the same utility, and one agent a utility at least (1 + ε) higher. This captures the notion that improvements smaller than (1 + ε) are negligible and should not be considered a breach of efficiency.
Pareto-efficiency and welfare-maximization
[edit]Suppose each agent i is assigned a positive weight ai. For every allocation x, define the welfare of x as the weighted sum of utilities of all agents in x:
Let xa be an allocation that maximizes the welfare over all allocations:
It is easy to show that the allocation xa is Pareto-efficient: since all weights are positive, any Pareto improvement would increase the sum, contradicting the definition of xa.
Japanese neo-Walrasian economist Takashi Negishi proved[20] that, under certain assumptions, the opposite is also true: for every Pareto-efficient allocation x, there exists a positive vector a such that x maximizes Wa. A shorter proof is provided by Hal Varian.[21]
Use in engineering
[edit]The notion of Pareto efficiency has been used in engineering.[22] Given a set of choices and a way of valuing them, the Pareto front (or Pareto set or Pareto frontier) is the set of choices that are Pareto-efficient. By restricting attention to the set of choices that are Pareto-efficient, a designer can make trade-offs within this set, rather than considering the full range of every parameter.[23]
Use in public policy
[edit]Modern microeconomic theory has drawn heavily upon the concept of Pareto efficiency for inspiration. Pareto and his successors have tended to describe this technical definition of optimal resource allocation in the context of it being an equilibrium that can theoretically be achieved within an abstract model of market competition. It has therefore very often been treated as a corroboration of Adam Smith's "invisible hand" notion. More specifically, it motivated the debate over "market socialism" in the 1930s.[4]
However, because the Pareto-efficient outcome is difficult to assess in the real world when issues including asymmetric information, signalling, adverse selection, and moral hazard are introduced, most people do not take the theorems of welfare economics as accurate descriptions of the real world. Therefore, the significance of the two welfare theorems of economics is in their ability to generate a framework that has dominated neoclassical thinking about public policy. That framework is that the welfare economics theorems allow the political economy to be studied in the following two situations: "market failure" and "the problem of redistribution".[24]
Analysis of "market failure" can be understood by the literature surrounding externalities. When comparing the "real" economy to the complete contingent markets economy (which is considered efficient), the inefficiencies become clear. These inefficiencies, or externalities, are then able to be addressed by mechanisms, including property rights and corrective taxes.[24]
Analysis of "the problem with redistribution" deals with the observed political question of how income or commodity taxes should be utilized. The theorem tells us that no taxation is Pareto-efficient and that taxation with redistribution is Pareto-inefficient. Because of this, most of the literature is focused on finding solutions where given there is a tax structure, how can the tax structure prescribe a situation where no person could be made better off by a change in available taxes.[24]
Use in biology
[edit]Pareto optimisation has also been studied in biological processes.[25] In bacteria, genes were shown to be either inexpensive to make (resource-efficient) or easier to read (translation-efficient). Natural selection acts to push highly expressed genes towards the Pareto frontier for resource use and translational efficiency.[26] Genes near the Pareto frontier were also shown to evolve more slowly (indicating that they are providing a selective advantage).[27]
Common misconceptions
[edit]It would be incorrect to treat Pareto efficiency as equivalent to societal optimization,[28] as the latter is a normative concept, which is a matter of interpretation that typically would account for the consequence of degrees of inequality of distribution.[29] An example would be the interpretation of one school district with low property tax revenue versus another with much higher revenue as a sign that more equal distribution occurs with the help of government redistribution.[30]
Criticism
[edit]Some commentators contest that Pareto efficiency could potentially serve as an ideological tool. With it implying that capitalism is self-regulated thereof, it is likely that the embedded structural problems such as unemployment would be treated as deviating from the equilibrium or norm, and thus neglected or discounted.[4]
Pareto efficiency does not require a totally equitable distribution of wealth, which is another aspect that draws in criticism.[31] An economy in which a wealthy few hold the vast majority of resources can be Pareto-efficient. A simple example is the distribution of a pie among three people. The most equitable distribution would assign one third to each person. However, the assignment of, say, a half section to each of two individuals and none to the third is also Pareto-optimal despite not being equitable, because none of the recipients could be made better off without decreasing someone else's share; and there are many other such distribution examples. An example of a Pareto-inefficient distribution of the pie would be allocation of a quarter of the pie to each of the three, with the remainder discarded.[32]
The liberal paradox elaborated by Amartya Sen shows that when people have preferences about what other people do, the goal of Pareto efficiency can come into conflict with the goal of individual liberty.[33]
Lastly, it is proposed that Pareto efficiency to some extent inhibited discussion of other possible criteria of efficiency. As Wharton School professor Ben Lockwood argues, one possible reason is that any other efficiency criteria established in the neoclassical domain will reduce to Pareto efficiency at the end.[4]
See also
[edit]- Admissible decision rule, analog in decision theory
- Arrow's impossibility theorem
- Bayesian efficiency
- Fundamental theorems of welfare economics
- Deadweight loss
- Economic efficiency
- Highest and best use
- Kaldor–Hicks efficiency
- Marginal utility
- Market failure, when a market result is not Pareto-optimal
- Maximal element, concept in order theory
- Maxima of a point set
- Multi-objective optimization
- Nash equilibrium
- Pareto-efficient envy-free division
- Social Choice and Individual Values for the "(weak) Pareto principle"
- TOTREP
- Welfare economics
References
[edit]- ^ "Martin J. Osborne". economics.utoronto.ca. Retrieved December 10, 2022.
- ^ proximedia. "Pareto Front". www.cenaero.be. Archived from the original on February 26, 2020. Retrieved October 8, 2018.
- ^ Black, J. D., Hashimzade, N., Myles, G. (eds.), A Dictionary of Economics, 5th ed. (Oxford: Oxford University Press, 2017), p. 459.
- ^ a b c d Lockwood, B. (2008). The New Palgrave Dictionary of Economics (2nd ed.). London: Palgrave Macmillan. ISBN 978-1-349-95121-5.
- ^ a b "Pareto Efficiency". Corporate Finance Institute. Retrieved December 10, 2022.
- ^ a b Watson, Joel (2013). Strategy: An Introduction to Game Theory (3rd ed.). W. W. Norton and Company.
- ^ a b Mas-Colell, A.; Whinston, Michael D.; Green, Jerry R. (1995), "Chapter 16: Equilibrium and its Basic Welfare Properties", Microeconomic Theory, Oxford University Press, ISBN 978-0-19-510268-0.
- ^ Gerard, Debreu (1959). "Valuation Equilibrium and Pareto Optimum". Proceedings of the National Academy of Sciences of the United States of America. 40 (7): 588–592. doi:10.1073/pnas.40.7.588. JSTOR 89325. PMC 528000. PMID 16589528.
- ^ Greenwald, B.; Stiglitz, J. E. (1986). "Externalities in economies with imperfect information and incomplete markets". Quarterly Journal of Economics. 101 (2): 229–264. doi:10.2307/1891114. JSTOR 1891114.
- ^ "The main difficulty is that, in contrast to the single-objective case where there is a total order relation between solutions, Pareto dominance is a partial order, which leads to solutions (and solution sets) being incomparable" Li, M., López-Ibáñez, M., & Yao, X. (Accepted/In press). Multi-Objective Archiving. IEEE Transactions on Evolutionary Computation. https://arxiv.org/pdf/2303.09685.pdf
- ^ a b Emmerich, M.T.M., Deutz, A.H. A tutorial on multiobjective optimization: fundamentals and evolutionary methods. Nat Comput 17, 585–609 (2018). https://doi.org/10.1007/s11047-018-9685-y
- ^ Mock, William B. T. (2011). "Pareto Optimality". Encyclopedia of Global Justice. pp. 808–809. doi:10.1007/978-1-4020-9160-5_341. ISBN 978-1-4020-9159-9.
- ^ Markey‐Towler, Brendan and John Foster. "Why economic theory has little to say about the causes and effects of inequality", School of Economics, University of Queensland, Australia, 21 February 2013, RePEc:qld:uq2004:476.
- ^ Magill, M., & Quinzii, M., Theory of Incomplete Markets, MIT Press, 2002, p. 104.
- ^ Barman, S., Krishnamurthy, S. K., & Vaish, R., "Finding Fair and Efficient Allocations", EC '18: Proceedings of the 2018 ACM Conference on Economics and Computation, June 2018.
- ^ Sandomirskiy, Fedor; Segal-Halevi, Erel (2022). "Efficient Fair Division with Minimal Sharing". Operations Research. 70 (3): 1762–1782. arXiv:1908.01669. doi:10.1287/opre.2022.2279. S2CID 247922344.
- ^ Bogomolnaia, Anna; Moulin, Hervé; Stong, Richard (June 1, 2005). "Collective choice under dichotomous preferences" (PDF). Journal of Economic Theory. 122 (2): 165–184. doi:10.1016/j.jet.2004.05.005. ISSN 0022-0531.
- ^ Nicola. (2013). Efficiency and Equity in Welfare Economics (1st ed. 2013). Springer Berlin Heidelberg : Imprint: Springer.
- ^ Ledyard, J. O. (1989). Market Failure. In: Eatwell, J., Milgate, M., Newman, P. (eds.) Allocation, Information and Markets. The New Palgrave. Palgrave Macmillan, London. doi:10.1007/978-1-349-20215-7_19.
- ^ Negishi, Takashi (1960). "Welfare Economics and Existence of an Equilibrium for a Competitive Economy". Metroeconomica. 12 (2–3): 92–97. doi:10.1111/j.1467-999X.1960.tb00275.x.
- ^ Varian, Hal R. (1976). "Two problems in the theory of fairness". Journal of Public Economics. 5 (3–4): 249–260. doi:10.1016/0047-2727(76)90018-9. hdl:1721.1/64180.
- ^ Goodarzi, E., Ziaei, M., & Hosseinipour, E. Z., Introduction to Optimization Analysis in Hydrosystem Engineering (Berlin/Heidelberg: Springer, 2014), pp. 111–148.
- ^ Jahan, A., Edwards, K. L., & Bahraminasab, M., Multi-criteria Decision Analysis, 2nd ed. (Amsterdam: Elsevier, 2013), pp. 63–65.
- ^ a b c Lockwood B. (2008) Pareto Efficiency. In: Palgrave Macmillan (eds.) The New Palgrave Dictionary of Economics. Palgrave Macmillan, London.
- ^ Moore, J. H., Hill, D. P., Sulovari, A., & Kidd, L. C., "Genetic Analysis of Prostate Cancer Using Computational Evolution, Pareto-Optimization and Post-processing", in R. Riolo, E. Vladislavleva, M. D. Ritchie, & J. H. Moore (eds.), Genetic Programming Theory and Practice X (Berlin/Heidelberg: Springer, 2013), pp. 87–102.
- ^ Eiben, A. E., & Smith, J. E., Introduction to Evolutionary Computing (Berlin/Heidelberg: Springer, 2003), pp. 166–169.
- ^ Seward, E. A., & Kelly, S., "Selection-driven cost-efficiency optimization of transcripts modulates gene evolutionary rate in bacteria", Genome Biology, Vol. 19, 2018.
- ^ Drèze, J., Essays on Economic Decisions Under Uncertainty (Cambridge: Cambridge University Press, 1987), pp. 358–364.
- ^ Backhaus, J. G., The Elgar Companion to Law and Economics (Cheltenham, UK / Northampton, MA: Edward Elgar, 2005), pp. 10–15.
- ^ Paulsen, M. B., "The Economics of the Public Sector: The Nature and Role of Public Policy in the Finance of Higher Education", in M. B. Paulsen, J. C. Smart (eds.) The Finance of Higher Education: Theory, Research, Policy, and Practice (New York: Agathon Press, 2001), pp. 95–132.
- ^ Bhushi, K. (ed.), Farm to Fingers: The Culture and Politics of Food in Contemporary India (Cambridge: Cambridge University Press, 2018), p. 222.
- ^ Wittman, D., Economic Foundations of Law and Organization (Cambridge: Cambridge University Press, 2006), p. 18.
- ^ Sen, A., Rationality and Freedom (Cambridge, MA / London: Belknep Press, 2004), pp. 92–94.
Pareto, V (1906). Manual of Political Economy. Oxford University Press. https://global.oup.com/academic/product/manual-of-political-economy-9780199607952?cc=ca&lang=en&.
Further reading
[edit]- Fudenberg, Drew; Tirole, Jean (1991). Game theory. Cambridge, Massachusetts: MIT Press. pp. 18–23. ISBN 9780262061414. Book preview.
- Bendor, Jonathan; Mookherjee, Dilip (April 2008). "Communitarian versus Universalistic norms". Quarterly Journal of Political Science. 3 (1): 33–61. doi:10.1561/100.00007028.
- Kanbur, Ravi (January–June 2005). "Pareto's revenge" (PDF). Journal of Social and Economic Development. 7 (1): 1–11.
- Ng, Yew-Kwang (2004). Welfare economics towards a more complete analysis. Basingstoke, Hampshire New York: Palgrave Macmillan. ISBN 9780333971215.
- Rubinstein, Ariel; Osborne, Martin J. (1994), "Introduction", in Rubinstein, Ariel; Osborne, Martin J. (eds.), A course in game theory, Cambridge, Massachusetts: MIT Press, pp. 6–7, ISBN 9780262650403 Book preview.
- Mathur, Vijay K. (Spring 1991). "How well do we know Pareto optimality?". The Journal of Economic Education. 22 (2): 172–178. doi:10.2307/1182422. JSTOR 1182422.
- Newbery, David M.G.; Stiglitz, Joseph E. (January 1984). "Pareto inferior trade". The Review of Economic Studies. 51 (1): 1–12. doi:10.2307/2297701. JSTOR 2297701.
| Books |
|
|---|---|
| Concepts | |
| Miscellaneous | |


































