2nd Johnson solid (6 faces)
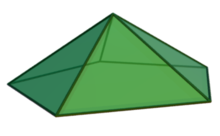
3D model of a pentagonal pyramid In geometry , a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point (the apex ). Like any pyramid , it is self-dual .
The regular pentagonal pyramid has a base that is a regular pentagon and lateral faces that are equilateral triangles . It is one of the Johnson solids (J 2
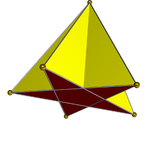
It can be seen as the "lid" of an icosahedron ; the rest of the icosahedron forms a gyroelongated pentagonal pyramid , J 11 .
More generally an order-2 vertex-uniform pentagonal pyramid can be defined with a regular pentagonal base and 5 isosceles triangle sides of any height.
Cartesian coordinates
The pentagonal pyramid can be seen as the "lid" of a regular icosahedron ; the rest of the icosahedron forms a gyroelongated pentagonal pyramid , J 11 . From the Cartesian coordinates of the icosahedron, Cartesian coordinates for a pentagonal pyramid with edge length 2 may be inferred as
(
1
,
0
,
τ
)
,
(
−
1
,
0
,
τ
)
,
(
0
,
τ
,
1
)
,
(
τ
,
1
,
0
)
,
(
τ
,
−
1
,
0
)
,
(
0
,
−
τ
,
1
)
{\displaystyle (1,0,\tau ),\,(-1,0,\tau ),\,(0,\tau ,1),\,(\tau ,1,0),(\tau ,-1,0),(0,-\tau ,1)}
where 𝜏 (sometimes written as φ ) is the golden ratio .[1]
The height H , from the midpoint of the pentagonal face to the apex, of a pentagonal pyramid with edge length a may therefore be computed as:
H
=
(
5
−
5
10
)
a
≈
0.52573
a
.
{\displaystyle H=\left({\sqrt {\frac {5-{\sqrt {5))}{10))}\right)a\approx 0.52573a.}
[2] Its surface area A can be computed as the area of the pentagonal base plus five times the area of one triangle:
A
=
a
2
2
5
2
(
10
+
5
+
75
+
30
5
)
≈
3.88554
⋅
a
2
.
{\displaystyle A={\frac {a^{2)){2)){\sqrt ((\frac {5}{2))\left(10+{\sqrt {5))+{\sqrt {75+30{\sqrt {5))))\right)))\approx 3.88554\cdot a^{2}.}
[3] [2] Its volume can be calculated as:
V
=
(
5
+
5
24
)
a
3
≈
0.30150
a
3
.
{\displaystyle V=\left({\frac {5+{\sqrt {5))}{24))\right)a^{3}\approx 0.30150a^{3}.}
[3]