
In mathematical analysis, the maximum and minimum[a] of a function are, respectively, the largest and smallest value taken by the function. Known generically as extremum,[b] they may be defined either within a given range (the local or relative extrema) or on the entire domain (the global or absolute extrema) of a function.[1][2][3] Pierre de Fermat was one of the first mathematicians to propose a general technique, adequality, for finding the maxima and minima of functions.
As defined in set theory, the maximum and minimum of a set are the greatest and least elements in the set, respectively. Unbounded infinite sets, such as the set of real numbers, have no minimum or maximum.
In statistics, the corresponding concept is the sample maximum and minimum.
Definition
[edit]A real-valued function f defined on a domain X has a global (or absolute) maximum point at x∗, if f(x∗) ≥ f(x) for all x in X. Similarly, the function has a global (or absolute) minimum point at x∗, if f(x∗) ≤ f(x) for all x in X. The value of the function at a maximum point is called the maximum value of the function, denoted , and the value of the function at a minimum point is called the minimum value of the function. Symbolically, this can be written as follows:
- is a global maximum point of function if
The definition of global minimum point also proceeds similarly.
If the domain X is a metric space, then f is said to have a local (or relative) maximum point at the point x∗, if there exists some ε > 0 such that f(x∗) ≥ f(x) for all x in X within distance ε of x∗. Similarly, the function has a local minimum point at x∗, if f(x∗) ≤ f(x) for all x in X within distance ε of x∗. A similar definition can be used when X is a topological space, since the definition just given can be rephrased in terms of neighbourhoods. Mathematically, the given definition is written as follows:
- Let be a metric space and function . Then is a local maximum point of function if such that
The definition of local minimum point can also proceed similarly.
In both the global and local cases, the concept of a strict extremum can be defined. For example, x∗ is a strict global maximum point if for all x in X with x ≠ x∗, we have f(x∗) > f(x), and x∗ is a strict local maximum point if there exists some ε > 0 such that, for all x in X within distance ε of x∗ with x ≠ x∗, we have f(x∗) > f(x). Note that a point is a strict global maximum point if and only if it is the unique global maximum point, and similarly for minimum points.
A continuous real-valued function with a compact domain always has a maximum point and a minimum point. An important example is a function whose domain is a closed and bounded interval of real numbers (see the graph above).
Search
[edit]Finding global maxima and minima is the goal of mathematical optimization. If a function is continuous on a closed interval, then by the extreme value theorem, global maxima and minima exist. Furthermore, a global maximum (or minimum) either must be a local maximum (or minimum) in the interior of the domain, or must lie on the boundary of the domain. So a method of finding a global maximum (or minimum) is to look at all the local maxima (or minima) in the interior, and also look at the maxima (or minima) of the points on the boundary, and take the largest (or smallest) one.
For differentiable functions, Fermat's theorem states that local extrema in the interior of a domain must occur at critical points (or points where the derivative equals zero).[4] However, not all critical points are extrema. One can often distinguish whether a critical point is a local maximum, a local minimum, or neither by using the first derivative test, second derivative test, or higher-order derivative test, given sufficient differentiability.[5]
For any function that is defined piecewise, one finds a maximum (or minimum) by finding the maximum (or minimum) of each piece separately, and then seeing which one is largest (or smallest).
Examples
[edit]
| Function | Maxima and minima |
|---|---|
| x2 | Unique global minimum at x = 0. |
| x3 | No global minima or maxima. Although the first derivative (3x2) is 0 at x = 0, this is an inflection point. (2nd derivative is 0 at that point.) |
| Unique global maximum at x = e. (See figure at right) | |
| x−x | Unique global maximum over the positive real numbers at x = 1/e. |
| x3/3 − x | First derivative x2 − 1 and second derivative 2x. Setting the first derivative to 0 and solving for x gives stationary points at −1 and +1. From the sign of the second derivative, we can see that −1 is a local maximum and +1 is a local minimum. This function has no global maximum or minimum. |
| |x| | Global minimum at x = 0 that cannot be found by taking derivatives, because the derivative does not exist at x = 0. |
| cos(x) | Infinitely many global maxima at 0, ±2π, ±4π, ..., and infinitely many global minima at ±π, ±3π, ±5π, .... |
| 2 cos(x) − x | Infinitely many local maxima and minima, but no global maximum or minimum. |
| cos(3πx)/x with 0.1 ≤ x ≤ 1.1 | Global maximum at x = 0.1 (a boundary), a global minimum near x = 0.3, a local maximum near x = 0.6, and a local minimum near x = 1.0. (See figure at top of page.) |
| x3 + 3x2 − 2x + 1 defined over the closed interval (segment) [−4,2] | Local maximum at x = −1−√15/3, local minimum at x = −1+√15/3, global maximum at x = 2 and global minimum at x = −4. |
For a practical example,[6] assume a situation where someone has feet of fencing and is trying to maximize the square footage of a rectangular enclosure, where is the length, is the width, and is the area:
The derivative with respect to is:
Setting this equal to
reveals that is our only critical point. Now retrieve the endpoints by determining the interval to which is restricted. Since width is positive, then , and since , that implies that . Plug in critical point , as well as endpoints and , into , and the results are and respectively.
Therefore, the greatest area attainable with a rectangle of feet of fencing is .[6]
Functions of more than one variable
[edit]


For functions of more than one variable, similar conditions apply. For example, in the (enlargeable) figure on the right, the necessary conditions for a local maximum are similar to those of a function with only one variable. The first partial derivatives as to z (the variable to be maximized) are zero at the maximum (the glowing dot on top in the figure). The second partial derivatives are negative. These are only necessary, not sufficient, conditions for a local maximum, because of the possibility of a saddle point. For use of these conditions to solve for a maximum, the function z must also be differentiable throughout. The second partial derivative test can help classify the point as a relative maximum or relative minimum. In contrast, there are substantial differences between functions of one variable and functions of more than one variable in the identification of global extrema. For example, if a bounded differentiable function f defined on a closed interval in the real line has a single critical point, which is a local minimum, then it is also a global minimum (use the intermediate value theorem and Rolle's theorem to prove this by contradiction). In two and more dimensions, this argument fails. This is illustrated by the function
whose only critical point is at (0,0), which is a local minimum with f(0,0) = 0. However, it cannot be a global one, because f(2,3) = −5.
Maxima or minima of a functional
[edit]If the domain of a function for which an extremum is to be found consists itself of functions (i.e. if an extremum is to be found of a functional), then the extremum is found using the calculus of variations.
In relation to sets
[edit]Maxima and minima can also be defined for sets. In general, if an ordered set S has a greatest element m, then m is a maximal element of the set, also denoted as . Furthermore, if S is a subset of an ordered set T and m is the greatest element of S with (respect to order induced by T), then m is a least upper bound of S in T. Similar results hold for least element, minimal element and greatest lower bound. The maximum and minimum function for sets are used in databases, and can be computed rapidly, since the maximum (or minimum) of a set can be computed from the maxima of a partition; formally, they are self-decomposable aggregation functions.
In the case of a general partial order, the least element (i.e., one that is smaller than all others) should not be confused with a minimal element (nothing is smaller). Likewise, a greatest element of a partially ordered set (poset) is an upper bound of the set which is contained within the set, whereas a maximal element m of a poset A is an element of A such that if m ≤ b (for any b in A), then m = b. Any least element or greatest element of a poset is unique, but a poset can have several minimal or maximal elements. If a poset has more than one maximal element, then these elements will not be mutually comparable.
In a totally ordered set, or chain, all elements are mutually comparable, so such a set can have at most one minimal element and at most one maximal element. Then, due to mutual comparability, the minimal element will also be the least element, and the maximal element will also be the greatest element. Thus in a totally ordered set, we can simply use the terms minimum and maximum.
If a chain is finite, then it will always have a maximum and a minimum. If a chain is infinite, then it need not have a maximum or a minimum. For example, the set of natural numbers has no maximum, though it has a minimum. If an infinite chain S is bounded, then the closure Cl(S) of the set occasionally has a minimum and a maximum, in which case they are called the greatest lower bound and the least upper bound of the set S, respectively.
Argument of the maximum
[edit]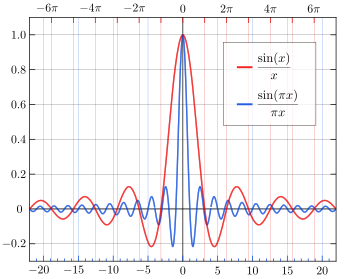
The unnormalised sinc function (red) has arg min of {−4.49, 4.49}, approximately, because it has 2 global minimum values of approximately −0.217 at x = ±4.49. However, the normalised sinc function (blue) has arg min of {−1.43, 1.43}, approximately, because their global minima occur at x = ±1.43, even though the minimum value is the same.[7]
See also
[edit]- Derivative test
- Infimum and supremum
- Limit superior and limit inferior
- Maximum-minimums identity
- Mechanical equilibrium
- Mex (mathematics)
- Sample maximum and minimum
- Saddle point
Notes
[edit]References
[edit]- ^ Stewart, James (2008). Calculus: Early Transcendentals (6th ed.). Brooks/Cole. ISBN 978-0-495-01166-8.
- ^ Larson, Ron; Edwards, Bruce H. (2009). Calculus (9th ed.). Brooks/Cole. ISBN 978-0-547-16702-2.
- ^ Thomas, George B.; Weir, Maurice D.; Hass, Joel (2010). Thomas' Calculus: Early Transcendentals (12th ed.). Addison-Wesley. ISBN 978-0-321-58876-0.
- ^ Weisstein, Eric W. "Minimum". mathworld.wolfram.com. Retrieved 2020-08-30.
- ^ Weisstein, Eric W. "Maximum". mathworld.wolfram.com. Retrieved 2020-08-30.
- ^ a b Garrett, Paul. "Minimization and maximization refresher".
- ^ "The Unnormalized Sinc Function Archived 2017-02-15 at the Wayback Machine", University of Sydney
- ^ For clarity, we refer to the input (x) as points and the output (y) as values; compare critical point and critical value.
External links
[edit]- Thomas Simpson's work on Maxima and Minima at Convergence
- Application of Maxima and Minima with sub pages of solved problems
- Jolliffe, Arthur Ernest (1911). . Encyclopædia Britannica. Vol. 17 (11th ed.). pp. 918–920.
| Precalculus | |||||
|---|---|---|---|---|---|
| Limits | |||||
| Differential calculus |
| ||||
| Integral calculus | |||||
| Vector calculus |
| ||||
| Multivariable calculus | |||||
| Sequences and series |
| ||||
| Special functions and numbers | |||||
| History of calculus | |||||
| Lists |
| ||||
| Miscellaneous topics |
| ||||









![{\displaystyle {\sqrt[{x}]{x))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/61b4a0a76158849854a302fc639dfc882ec16008)























