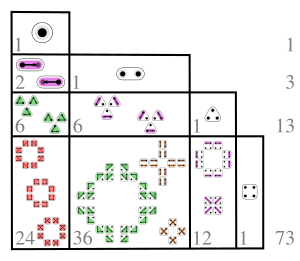
In mathematics, the (signed and unsigned) Lah numbers are coefficients expressing rising factorials in terms of falling factorials and vice versa. They were discovered by Ivo Lah in 1954.^[1][2] Explicitly, the unsigned Lah numbers ${\displaystyle L(n,k)}$ are given by the formula involving the binomial coefficient

$${\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!))}$$

for ${\displaystyle n\geq k\geq 1}$.

Unsigned Lah numbers have an interesting meaning in combinatorics: they count the number of ways a set of ${\textstyle n}$ elements can be partitioned into ${\textstyle k}$ nonempty linearly ordered subsets.^[3] Lah numbers are related to Stirling numbers.^[4]

For ${\textstyle n\geq 1}$, the Lah number ${\textstyle L(n,1)}$ is equal to the factorial ${\textstyle n!}$ in the interpretation above, the only partition of ${\textstyle \{1,2,3\))$ into 1 set can have its set ordered in 6 ways:$${\displaystyle \{(1,2,3)\},\{(1,3,2)\},\{(2,1,3)\},\{(2,3,1)\},\{(3,1,2)\},\{(3,2,1)\))$$${\textstyle L(3,2)}$ is equal to 6, because there are six partitions of ${\textstyle \{1,2,3\))$ into two ordered parts:$${\displaystyle \{1,(2,3)\},\{1,(3,2)\},\{2,(1,3)\},\{2,(3,1)\},\{3,(1,2)\},\{3,(2,1)\))$$${\textstyle L(n,n)}$ is always 1 because the only way to partition ${\textstyle \{1,2,\ldots ,n\))$ into ${\displaystyle n}$ non-empty subsets results in subsets of size 1, that can only be permuted in one way. In the more recent literature,^[5][6] Karamata–Knuth style notation has taken over. Lah numbers are now often written as$${\displaystyle L(n,k)=\left\lfloor {n \atop k}\right\rfloor }$$

Below is a table of values for the Lah numbers:

The row sums are ${\textstyle 1,1,3,13,73,501,4051,37633,\dots }$ (sequence A000262 in the OEIS).

Let ${\textstyle x^{(n)))$ represent the rising factorial ${\textstyle x(x+1)(x+2)\cdots (x+n-1)}$ and let ${\textstyle (x)_{n))$ represent the falling factorial ${\textstyle x(x-1)(x-2)\cdots (x-n+1)}$. The Lah numbers are the coefficients that express each of these families of polynomials in terms of the other. Explicitly,$${\displaystyle x^{(n)}=\sum _{k=0}^{n}L(n,k)(x)_{k))$$and$${\displaystyle (x)_{n}=\sum _{k=0}^{n}(-1)^{n-k}L(n,k)x^{(k)}.}$$For example,$${\displaystyle x(x+1)(x+2)={\color {red}6}x+{\color {red}6}x(x-1)+{\color {red}1}x(x-1)(x-2)}$$and$${\displaystyle x(x-1)(x-2)={\color {red}6}x-{\color {red}6}x(x+1)+{\color {red}1}x(x+1)(x+2),}$$

where the coefficients 6, 6, and 1 are exactly the Lah numbers ${\displaystyle L(3,1)}$, ${\displaystyle L(3,2)}$, and ${\displaystyle L(3,3)}$.

The Lah numbers satisfy a variety of identities and relations.

In Karamata–Knuth notation for Stirling numbers$${\displaystyle L(n,k)=\sum _{j=k}^{n}\left[{n \atop j}\right]\left\((j \atop k}\right\))$$where ${\textstyle \left[{n \atop j}\right]}$ are the Stirling numbers of the first kind and ${\textstyle \left\((j \atop k}\right\))$ are the Stirling numbers of the second kind.

${\displaystyle L(n,k)={n-1 \choose k-1}{\frac {n!}{k!))={n \choose k}{\frac {(n-1)!}{(k-1)!))={n \choose k}{n-1 \choose k-1}(n-k)!}$

${\displaystyle L(n,k)={\frac {n!(n-1)!}{k!(k-1)!))\cdot {\frac {1}{(n-k)!))=\left({\frac {n!}{k!))\right)^{2}{\frac {k}{n(n-k)!))}$

${\displaystyle k(k+1)L(n,k+1)=(n-k)L(n,k)}$, for ${\displaystyle k>0}$.

The Lah numbers satisfy the recurrence relations$${\displaystyle {\begin{aligned}L(n+1,k)&=(n+k)L(n,k)+L(n,k-1)\\&=k(k+1)L(n,k+1)+2kL(n,k)+L(n,k-1)\end{aligned))}$$where ${\displaystyle L(n,0)=\delta _{n))$, the Kronecker delta, and ${\displaystyle L(n,k)=0}$ for all ${\displaystyle k>n}$.

${\displaystyle \sum _{n\geq k}L(n,k){\frac {x^{n)){n!))={\frac {1}{k!))\left({\frac {x}{1-x))\right)^{k))$

The n-th derivative of the function ${\displaystyle e^{\frac {1}{x))}$ can be expressed with the Lah numbers, as follows^[7]$${\displaystyle {\frac ((\textrm {d))^{n))((\textrm {d))x^{n))}e^{\frac {1}{x))=(-1)^{n}\sum _{k=1}^{n}{\frac {L(n,k)}{x^{n+k))}\cdot e^{\frac {1}{x)).}$$For example,

${\displaystyle {\frac {\textrm {d))((\textrm {d))x))e^{\frac {1}{x))=-{\frac {1}{x^{2))}\cdot e^{\frac {1}{x))}$

${\displaystyle {\frac ((\textrm {d))^{2))((\textrm {d))x^{2))}e^{\frac {1}{x))={\frac {\textrm {d))((\textrm {d))x))\left(-{\frac {1}{x^{2))}e^{\frac {1}{x))\right)=-{\frac {-2}{x^{3))}\cdot e^{\frac {1}{x))-{\frac {1}{x^{2))}\cdot {\frac {-1}{x^{2))}\cdot e^{\frac {1}{x))=\left({\frac {2}{x^{3))}+{\frac {1}{x^{4))}\right)\cdot e^{\frac {1}{x))}$

${\displaystyle {\frac ((\textrm {d))^{3))((\textrm {d))x^{3))}e^{\frac {1}{x))={\frac {\textrm {d))((\textrm {d))x))\left(\left({\frac {2}{x^{3))}+{\frac {1}{x^{4))}\right)\cdot e^{\frac {1}{x))\right)=\left({\frac {-6}{x^{4))}+{\frac {-4}{x^{5))}\right)\cdot e^{\frac {1}{x))+\left({\frac {2}{x^{3))}+{\frac {1}{x^{4))}\right)\cdot {\frac {-1}{x^{2))}\cdot e^{\frac {1}{x))=-\left({\frac {6}{x^{4))}+{\frac {6}{x^{5))}+{\frac {1}{x^{6))}\right)\cdot e^{\frac {1}{x))}$

Generalized Laguerre polynomials ${\displaystyle L_{n}^{(\alpha )}(x)}$ are linked to Lah numbers upon setting ${\displaystyle \alpha =-1}$$${\displaystyle n!L_{n}^{(-1)}(x)=\sum _{k=0}^{n}L(n,k)(-x)^{k))$$This formula is the default Laguerre polynomial in Umbral calculus convention.^[8]

In recent years, Lah numbers have been used in steganography for hiding data in images. Compared to alternatives such as DCT, DFT and DWT, it has lower complexity of calculation—${\displaystyle O(n\log n)}$—of their integer coefficients.^[9][10] The Lah and Laguerre transforms naturally arise in the perturbative description of the chromatic dispersion.^[11][12] In Lah-Laguerre optics, such an approach tremendously speeds up optimization problems.

• Stirling numbers
• Pascal matrix

• The signed and unsigned Lah numbers are respectively (sequence A008297 in the OEIS) and (sequence A105278 in the OEIS)