
A centered octagonal number is a centered figurate number that represents an octagon with a dot in the center and all other dots surrounding the center dot in successive octagonal layers.[1] The centered octagonal numbers are the same as the odd square numbers.[2] Thus, the nth odd square number and tth centered octagonal number is given by the formula
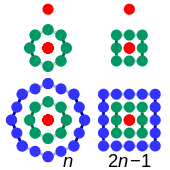
The first few centered octagonal numbers are[2]
- 1, 9, 25, 49, 81, 121, 169, 225, 289, 361, 441, 529, 625, 729, 841, 961, 1089, 1225
Calculating Ramanujan's tau function on a centered octagonal number yields an odd number, whereas for any other number the function yields an even number.[2]
is the number of 2x2 matrices with elements from 0 to n that their determinant is twice their permanent.

