Motzkin number| Named after | Theodore Motzkin |
|---|
| Publication year | 1948 |
|---|
| Author of publication | Theodore Motzkin |
|---|
| No. of known terms | infinity |
|---|
| Formula | see Properties |
|---|
| First terms | 1, 1, 2, 4, 9, 21, 51 |
|---|
| OEIS index | |
|---|
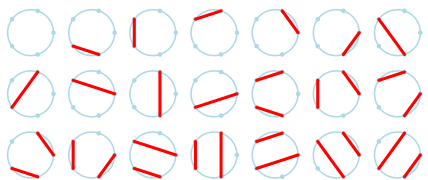
In mathematics, the nth Motzkin number is the number of different ways of drawing non-intersecting chords between n points on a circle (not necessarily touching every point by a chord). The Motzkin numbers are named after Theodore Motzkin and have diverse applications in geometry, combinatorics and number theory.
The Motzkin numbers  for
for  form the sequence:
form the sequence:
- 1, 1, 2, 4, 9, 21, 51, 127, 323, 835, ... (sequence A001006 in the OEIS)
Examples
The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle (M4 = 9):

The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle (M5 = 21):
Properties
The Motzkin numbers satisfy the recurrence relations

The Motzkin numbers can be expressed in terms of binomial coefficients and Catalan numbers:

and inversely,[1]

This gives

The generating function  of the Motzkin numbers satisfies
of the Motzkin numbers satisfies

and is explicitly expressed as

An integral representation of Motzkin numbers is given by
 .
.
They have the asymptotic behaviour
 .
.
A Motzkin prime is a Motzkin number that is prime. Four such primes are known:
- 2, 127, 15511, 953467954114363 (sequence A092832 in the OEIS)
Combinatorial interpretations
The Motzkin number for n is also the number of positive integer sequences of length n − 1 in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1. Equivalently, the Motzkin number for n is the number of positive integer sequences of length n + 1 in which the opening and ending elements are 1, and the difference between any two consecutive elements is −1, 0 or 1.
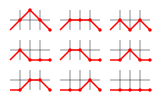
Also, the Motzkin number for n gives the number of routes on the upper right quadrant of a grid from coordinate (0, 0) to coordinate (n, 0) in n steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the y = 0 axis.
For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):
There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by Donaghey & Shapiro (1977) in their survey of Motzkin numbers.
Guibert, Pergola & Pinzani (2001) showed that vexillary involutions are enumerated by Motzkin numbers.













