Part of a series on
Machine learning and data mining
Paradigms Supervised learning Unsupervised learning Online learning Batch learning Semi-supervised learning Self-supervised learning Reinforcement learning
Problems Classification Regression Clustering dimension reduction density estimation Anomaly detection Data Cleaning AutoML Association rules Structured prediction Feature engineering Feature learning Learning to rank Grammar induction
Supervised learning (classification • regression) Decision trees Ensembles Bagging Boosting Random forest k-NN Linear regression Naive Bayes Artificial neural networks Logistic regression Perceptron Relevance vector machine (RVM) Support vector machine (SVM)
Clustering BIRCH CURE Hierarchical k-means Fuzzy Expectation–maximization (EM) DBSCAN OPTICS Mean shift
Dimensionality reduction Factor analysis CCA ICA LDA NMF PCA PGD t-SNE SDL
Structured prediction Graphical models Bayes net Conditional random field Hidden Markov
Anomaly detection RANSAC k-NN Local outlier factor Isolation forest
Artificial neural network Autoencoder Cognitive computing Deep learning DeepDream Multilayer perceptron RNN LSTM GRU ESN reservoir computing Restricted Boltzmann machine GAN SOM Convolutional neural network U-Net Transformer Vision Spiking neural network Memtransistor Electrochemical RAM (ECRAM)
Reinforcement learning Q-learning SARSA Temporal difference (TD) Multi-agent Self-play
Learning with humans Active learning Crowdsourcing Human-in-the-loop
Model diagnostics Learning curve
Theory Kernel machines Bias–variance tradeoff Computational learning theory Empirical risk minimization Occam learning PAC learning Statistical learning VC theory
Machine-learning venues NeurIPS ICML ICLR ML JMLR
Related articles Glossary of artificial intelligence List of datasets for machine-learning research Outline of machine learning
v t e

Logistic activation function

In artificial neural networks, the activation function of a node defines the output of that node given an input or set of inputs. A standard integrated circuit can be seen as a digital network of activation functions that can be "ON" (1) or "OFF" (0), depending on input. This is similar to the linear perceptron in neural networks. However, only nonlinear activation functions allow such networks to compute nontrivial problems using only a small number of nodes, and such activation functions are called nonlinearities.^[1]

Classification of activation functions

The most common activation functions can be divided in three categories: ridge functions, radial functions and fold functions.

An activation function ${\displaystyle f}$ is saturating if ${\displaystyle \lim _{|v|\to \infty }|\nabla f(v)|=0}$. It is nonsaturating if it is not saturating. Non-saturating activation functions, such as ReLU, may be better than saturating activation functions, as they don't suffer from vanishing gradient.^[2]

Ridge activation functions

Ridge functions are multivariate functions acting on a linear combination of the input variables. Often used examples include:

• Linear activation: ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$,
• ReLU activation: ${\displaystyle \phi (\mathbf {v} )=\max(0,a+\mathbf {v} '\mathbf {b} )}$,
• Heaviside activation: ${\displaystyle \phi (\mathbf {v} )=1_{a+\mathbf {v} '\mathbf {b} >0))$,
• Logistic activation: ${\displaystyle \phi (\mathbf {v} )=(1+\exp(-a-\mathbf {v} '\mathbf {b} ))^{-1))$.

In biologically inspired neural networks, the activation function is usually an abstraction representing the rate of action potential firing in the cell.^[3] In its simplest form, this function is binary—that is, either the neuron is firing or not. The function looks like ${\displaystyle \phi (\mathbf {v} )=U(a+\mathbf {v} '\mathbf {b} )}$, where ${\displaystyle U}$ is the Heaviside step function.

A line of positive slope may be used to reflect the increase in firing rate that occurs as input current increases. Such a function would be of the form ${\displaystyle \phi (\mathbf {v} )=a+\mathbf {v} '\mathbf {b} }$.

Rectified linear unit and Gaussian error linear unit activation functions

Neurons also cannot fire faster than a certain rate, motivating sigmoid activation functions whose range is a finite interval.

Radial activation functions

A special class of activation functions known as radial basis functions (RBFs) are used in RBF networks, which are extremely efficient as universal function approximators. These activation functions can take many forms, but they are usually found as one of the following functions:

• Gaussian: ${\displaystyle \,\phi (\mathbf {v} )=\exp \left(-{\frac {\|\mathbf {v} -\mathbf {c} \|^{2)){2\sigma ^{2))}\right)}$
• Multiquadratics: ${\displaystyle \,\phi (\mathbf {v} )={\sqrt {\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2))))$
• Inverse multiquadratics: ${\displaystyle \,\phi (\mathbf {v} )=\left(\|\mathbf {v} -\mathbf {c} \|^{2}+a^{2}\right)^{-{\frac {1}{2))))$
• Polyharmonic splines

where ${\displaystyle \mathbf {c} }$ is the vector representing the function center and ${\displaystyle a}$ and ${\displaystyle \sigma }$ are parameters affecting the spread of the radius.

Folding activation functions

Folding activation functions are extensively used in the pooling layers in convolutional neural networks, and in output layers of multiclass classification networks. These activations perform aggregation over the inputs, such as taking the mean, minimum or maximum. In multiclass classification the softmax activation is often used.

Comparison of activation functions

There are numerous activation functions. Hinton et al.'s seminal 2012 paper on automatic speech recognition uses a logistic sigmoid activation function.^[4] The seminal 2012 AlexNet computer vision architecture uses the ReLU activation function, as did the seminal 2015 computer vision architecture ResNet. The seminal 2018 language processing model BERT uses a smooth version of the ReLU, the GELU.^[5]

Aside from their empirical performance, activation functions also have different mathematical properties:

Nonlinear

When the activation function is non-linear, then a two-layer neural network can be proven to be a universal function approximator.^[6] This is known as the Universal Approximation Theorem. The identity activation function does not satisfy this property. When multiple layers use the identity activation function, the entire network is equivalent to a single-layer model.

Range

When the range of the activation function is finite, gradient-based training methods tend to be more stable, because pattern presentations significantly affect only limited weights. When the range is infinite, training is generally more efficient because pattern presentations significantly affect most of the weights. In the latter case, smaller learning rates are typically necessary.^{[citation needed]}

Continuously differentiable

This property is desirable (ReLU is not continuously differentiable and has some issues with gradient-based optimization, but it is still possible) for enabling gradient-based optimization methods. The binary step activation function is not differentiable at 0, and it differentiates to 0 for all other values, so gradient-based methods can make no progress with it.^[7]

These properties do not decisively influence performance, nor are they the only mathematical properties that may be useful. For instance, the strictly positive range of the softplus makes it suitable for predicting variances in variational autoencoders.

Table of activation functions

The following table compares the properties of several activation functions that are functions of one fold x from the previous layer or layers:

Name	Plot	Function, ${\displaystyle g(x)}$	Derivative of ${\displaystyle g}$, ${\displaystyle g'(x)}$	Range	Order of continuity
Identity		${\displaystyle x}$	${\displaystyle 1}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{\infty ))$
Binary step		${\displaystyle {\begin{cases}0&{\text{if ))x<0\\1&{\text{if ))x\geq 0\end{cases))}$	${\displaystyle 0}$	${\displaystyle \{0,1\))$	${\displaystyle C^{-1))$
Logistic, sigmoid, or soft step		${\displaystyle \sigma (x)\doteq {\frac {1}{1+e^{-x))))$	${\displaystyle g(x)(1-g(x))}$	${\displaystyle (0,1)}$	${\displaystyle C^{\infty ))$
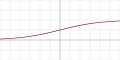
Hyperbolic tangent (tanh)		${\displaystyle \tanh(x)\doteq {\frac {e^{x}-e^{-x)){e^{x}+e^{-x))))$	${\displaystyle 1-g(x)^{2))$	${\displaystyle (-1,1)}$	${\displaystyle C^{\infty ))$
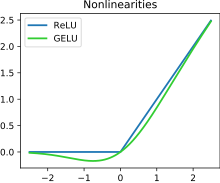
Rectified linear unit (ReLU)[8]		${\displaystyle {\begin{aligned}(x)^{+}\doteq {}&{\begin{cases}0&{\text{if ))x\leq 0\\x&{\text{if ))x>0\end{cases))\\={}&\max(0,x)=x{\textbf {1))_{x>0}\end{aligned))}$	${\displaystyle {\begin{cases}0&{\text{if ))x<0\\1&{\text{if ))x>0\\{\text{undefined))&{\text{if ))x=0\end{cases))}$	${\displaystyle [0,\infty )}$	${\displaystyle C^{0))$
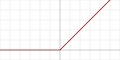
Gaussian Error Linear Unit (GELU)[5]		${\displaystyle {\begin{aligned}&{\frac {1}{2))x\left(1+{\text{erf))\left({\frac {x}{\sqrt {2))}\right)\right)\\{}={}&x\Phi (x)\end{aligned))}$	${\displaystyle \Phi (x)+x\phi (x)}$	${\displaystyle (-0.17\ldots ,\infty )}$	${\displaystyle C^{\infty ))$
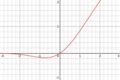
Softplus[9]		${\displaystyle \ln \left(1+e^{x}\right)}$	${\displaystyle {\frac {1}{1+e^{-x))))$	${\displaystyle (0,\infty )}$	${\displaystyle C^{\infty ))$
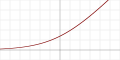
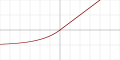
Exponential linear unit (ELU)[10]		${\displaystyle {\begin{cases}\alpha \left(e^{x}-1\right)&{\text{if ))x\leq 0\\x&{\text{if ))x>0\end{cases))}$ with parameter ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha e^{x}&{\text{if ))x<0\\1&{\text{if ))x>0\\1&{\text{if ))x=0{\text{ and ))\alpha =1\end{cases))}$	${\displaystyle (-\alpha ,\infty )}$	${\displaystyle {\begin{cases}C^{1}&{\text{if ))\alpha =1\\C^{0}&{\text{otherwise))\end{cases))}$
Scaled exponential linear unit (SELU)[11]		${\displaystyle \lambda {\begin{cases}\alpha (e^{x}-1)&{\text{if ))x<0\\x&{\text{if ))x\geq 0\end{cases))}$ with parameters ${\displaystyle \lambda =1.0507}$ and ${\displaystyle \alpha =1.67326}$	${\displaystyle \lambda {\begin{cases}\alpha e^{x}&{\text{if ))x<0\\1&{\text{if ))x\geq 0\end{cases))}$	${\displaystyle (-\lambda \alpha ,\infty )}$	${\displaystyle C^{0))$
Leaky rectified linear unit (Leaky ReLU)[12]		${\displaystyle {\begin{cases}0.01x&{\text{if ))x<0\\x&{\text{if ))x\geq 0\end{cases))}$	${\displaystyle {\begin{cases}0.01&{\text{if ))x<0\\1&{\text{if ))x\geq 0\\{\text{undefined))&{\text{if ))x=0\end{cases))}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0))$
Parametric rectified linear unit (PReLU)[13]		${\displaystyle {\begin{cases}\alpha x&{\text{if ))x<0\\x&{\text{if ))x\geq 0\end{cases))}$ with parameter ${\displaystyle \alpha }$	${\displaystyle {\begin{cases}\alpha &{\text{if ))x<0\\1&{\text{if ))x\geq 0\end{cases))}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0))$
Sigmoid linear unit (SiLU,[5] Sigmoid shrinkage,[14] SiL,[15] or Swish-‍1[16])		${\displaystyle {\frac {x}{1+e^{-x))))$	${\displaystyle {\frac {1+e^{-x}+xe^{-x)){\left(1+e^{-x}\right)^{2))))$	${\displaystyle [-0.278\ldots ,\infty )}$	${\displaystyle C^{\infty ))$
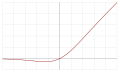
Gaussian		${\displaystyle e^{-x^{2))}$	${\displaystyle -2xe^{-x^{2))}$	${\displaystyle (0,1]}$	${\displaystyle C^{\infty ))$

The following table lists activation functions that are not functions of a single fold x from the previous layer or layers:

Name	Equation, ${\displaystyle g_{i}\left({\vec {x))\right)}$	Derivatives, ${\displaystyle {\frac {\partial g_{i}\left({\vec {x))\right)}{\partial x_{j))))$	Range	Order of continuity
Softmax	${\displaystyle {\frac {e^{x_{i))}{\sum _{j=1}^{J}e^{x_{j))))}$    for i = 1, …, J	${\displaystyle g_{i}\left({\vec {x))\right)\left(\delta _{ij}-g_{j}\left({\vec {x))\right)\right)}$[1][2]	${\displaystyle (0,1)}$	${\displaystyle C^{\infty ))$
Maxout[17]	${\displaystyle \max _{i}x_{i))$	${\displaystyle {\begin{cases}1&{\text{if ))j={\underset {i}{\operatorname {argmax} ))\,x_{i}\\0&{\text{if ))j\neq {\underset {i}{\operatorname {argmax} ))\,x_{i}\end{cases))}$	${\displaystyle (-\infty ,\infty )}$	${\displaystyle C^{0))$

^ Here, ${\displaystyle \delta _{ij))$ is the Kronecker delta.

^ For instance, ${\displaystyle j}$ could be iterating through the number of kernels of the previous neural network layer while ${\displaystyle i}$ iterates through the number of kernels of the current layer.