Neural networks
Tasks vs. methods

| Part of a series on |
| Machine learning and data mining |
|---|
Neural network tasks are often categorized as discriminative (recognition) or generative (imagination). Often but not always, discriminative tasks use supervised methods and generative tasks use unsupervised (see Venn diagram); however, the separation is very hazy. For example, object recognition favors supervised learning but unsupervised learning can also cluster objects into groups. Furthermore, as progress marches onward some tasks employ both methods, and some tasks swing from one to another. For example, image recognition started off as heavily supervised, but became hybrid by employing unsupervised pre-training, and then moved towards supervision again with the advent of dropout, ReLU, and adaptive learning rates.
Training
During the learning phase, an unsupervised network tries to mimic the data it's given and uses the error in its mimicked output to correct itself (i.e. correct its weights and biases). Sometimes the error is expressed as a low probability that the erroneous output occurs, or it might be expressed as an unstable high energy state in the network.
In contrast to supervised methods' dominant use of backpropagation, unsupervised learning also employs other methods including: Hopfield learning rule, Boltzmann learning rule, Contrastive Divergence, Wake Sleep, Variational Inference, Maximum Likelihood, Maximum A Posteriori, Gibbs Sampling, and backpropagating reconstruction errors or hidden state reparameterizations. See the table below for more details.
Energy
An energy function is a macroscopic measure of a network's activation state. In Boltzmann machines, it plays the role of the Cost function. This analogy with physics is inspired by Ludwig Boltzmann's analysis of a gas' macroscopic energy from the microscopic probabilities of particle motion , where k is the Boltzmann constant and T is temperature. In the RBM network the relation is ,[3] where and vary over every possible activation pattern and . To be more precise, , where is an activation pattern of all neurons (visible and hidden). Hence, some early neural networks bear the name Boltzmann Machine. Paul Smolensky calls the Harmony. A network seeks low energy which is high Harmony.
Networks
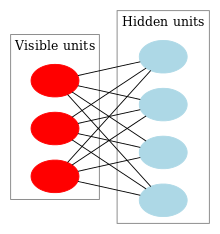
This table shows connection diagrams of various unsupervised networks, the details of which will be given in the section Comparison of Networks. Circles are neurons and edges between them are connection weights. As network design changes, features are added on to enable new capabilities or removed to make learning faster. For instance, neurons change between deterministic (Hopfield) and stochastic (Boltzmann) to allow robust output, weights are removed within a layer (RBM) to hasten learning, or connections are allowed to become asymmetric (Helmholtz).
| Hopfield | Boltzmann | RBM | Stacked Boltzmann |
|---|---|---|---|
 |
 |
 |
 |
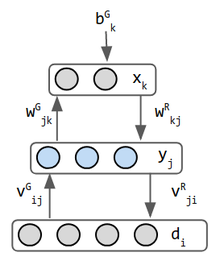
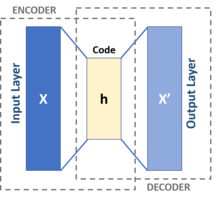
| Helmholtz | Autoencoder | VAE |
|---|---|---|
 |
 |
 |
Of the networks bearing people's names, only Hopfield worked directly with neural networks. Boltzmann and Helmholtz came before artificial neural networks, but their work in physics and physiology inspired the analytical methods that were used.
History
| 1969 | Perceptrons by Minsky & Papert shows a perceptron without hidden layers fails on XOR |
| 1970s | (approximate dates) First AI winter |
| 1974 | Ising magnetic model proposed by WA Little for cognition |
| 1980 | Fukushima introduces the neocognitron, which is later called a convolutional neural network. It is mostly used in SL, but deserves a mention here. |
| 1982 | Ising variant Hopfield net described as CAMs and classifiers by John Hopfield. |
| 1983 | Ising variant Boltzmann machine with probabilistic neurons described by Hinton & Sejnowski following Sherington & Kirkpatrick's 1975 work. |
| 1986 | Paul Smolensky publishes Harmony Theory, which is an RBM with practically the same Boltzmann energy function. Smolensky did not give a practical training scheme. Hinton did in mid-2000s. |
| 1995 | Schmidthuber introduces the LSTM neuron for languages. |
| 1995 | Dayan & Hinton introduces Helmholtz machine |
| 1995-2005 | (approximate dates) Second AI winter |
| 2013 | Kingma, Rezende, & co. introduced Variational Autoencoders as Bayesian graphical probability network, with neural nets as components. |
Specific Networks
Here, we highlight some characteristics of select networks. The details of each are given in the comparison table below.
- Hopfield Network
- Ferromagnetism inspired Hopfield networks. A neuron correspond to an iron domain with binary magnetic moments Up and Down, and neural connections correspond to the domain's influence on each other. Symmetric connections enable a global energy formulation. During inference the network updates each state using the standard activation step function. Symmetric weights and the right energy functions guarantees convergence to a stable activation pattern. Asymmetric weights are difficult to analyze. Hopfield nets are used as Content Addressable Memories (CAM).
- Boltzmann Machine
- These are stochastic Hopfield nets. Their state value is sampled from this pdf as follows: suppose a binary neuron fires with the Bernoulli probability p(1) = 1/3 and rests with p(0) = 2/3. One samples from it by taking a uniformly distributed random number y, and plugging it into the inverted cumulative distribution function, which in this case is the step function thresholded at 2/3. The inverse function = { 0 if x <= 2/3, 1 if x > 2/3 }.
- Sigmoid Belief Net
- Introduced by Radford Neal in 1992, this network applies ideas from probabilistic graphical models to neural networks. A key difference is that nodes in graphical models have pre-assigned meanings, whereas Belief Net neurons' features are determined after training. The network is a sparsely connected directed acyclic graph composed of binary stochastic neurons. The learning rule comes from Maximum Likelihood on p(X): Δwij sj * (si - pi), where pi = 1 / ( 1 + eweighted inputs into neuron i ). sj's are activations from an unbiased sample of the posterior distribution and this is problematic due to the Explaining Away problem raised by Judea Perl. Variational Bayesian methods uses a surrogate posterior and blatantly disregard this complexity.
- Deep Belief Network
- Introduced by Hinton, this network is a hybrid of RBM and Sigmoid Belief Network. The top 2 layers is an RBM and the second layer downwards form a sigmoid belief network. One trains it by the stacked RBM method and then throw away the recognition weights below the top RBM. As of 2009, 3-4 layers seems to be the optimal depth.[4]
- Helmholtz machine
- These are early inspirations for the Variational Auto Encoders. Its 2 networks combined into one—forward weights operates recognition and backward weights implements imagination. It is perhaps the first network to do both. Helmholtz did not work in machine learning but he inspired the view of "statistical inference engine whose function is to infer probable causes of sensory input".[5] the stochastic binary neuron outputs a probability that its state is 0 or 1. The data input is normally not considered a layer, but in the Helmholtz machine generation mode, the data layer receives input from the middle layer and has separate weights for this purpose, so it is considered a layer. Hence this network has 3 layers.
- Variational autoencoder
- These are inspired by Helmholtz machines and combines probability network with neural networks. An Autoencoder is a 3-layer CAM network, where the middle layer is supposed to be some internal representation of input patterns. The encoder neural network is a probability distribution qφ(z given x) and the decoder network is pθ(x given z). The weights are named phi & theta rather than W and V as in Helmholtz—a cosmetic difference. These 2 networks here can be fully connected, or use another NN scheme.
Comparison of networks
| Hopfield | Boltzmann | RBM | Stacked RBM | Helmholtz | Autoencoder | VAE | |
|---|---|---|---|---|---|---|---|
| Usage & notables | CAM, traveling salesman problem | CAM. The freedom of connections makes this network difficult to analyze. | pattern recognition. used in MNIST digits and speech. | recognition & imagination. trained with unsupervised pre-training and/or supervised fine tuning. | imagination, mimicry | language: creative writing, translation. vision: enhancing blurry images | generate realistic data |
| Neuron | deterministic binary state. Activation = { 0 (or -1) if x is negative, 1 otherwise } | stochastic binary Hopfield neuron | ← same. (extended to real-valued in mid 2000s) | ← same | ← same | language: LSTM. vision: local receptive fields. usually real valued relu activation. | middle layer neurons encode means & variances for Gaussians. In run mode (inference), the output of the middle layer are sampled values from the Gaussians. |
| Connections | 1-layer with symmetric weights. No self-connections. | 2-layers. 1-hidden & 1-visible. symmetric weights. | ← same. no lateral connections within a layer. |
top layer is undirected, symmetric. other layers are 2-way, asymmetric. | 3-layers: asymmetric weights. 2 networks combined into 1. | 3-layers. The input is considered a layer even though it has no inbound weights. recurrent layers for NLP. feedforward convolutions for vision. input & output have the same neuron counts. | 3-layers: input, encoder, distribution sampler decoder. the sampler is not considered a layer |
| Inference & energy | Energy is given by Gibbs probability measure : | ← same | ← same | minimize KL divergence | inference is only feed-forward. previous UL networks ran forwards AND backwards | minimize error = reconstruction error - KLD | |
| Training | Δwij = si*sj, for +1/-1 neuron | Δwij = e*(pij - p'ij). This is derived from minimizing KLD. e = learning rate, p' = predicted and p = actual distribution. | Δwij = e*( < vi hj >data - < vi hj >equilibrium ). This is a form of contrastive divergence w/ Gibbs Sampling. "<>" are expectations. | ← similar. train 1-layer at a time. approximate equilibrium state with a 3-segment pass. no back propagation. | wake-sleep 2 phase training | back propagate the reconstruction error | reparameterize hidden state for backprop |
| Strength | resembles physical systems so it inherits their equations | ← same. hidden neurons act as internal representatation of the external world | faster more practical training scheme than Boltzmann machines | trains quickly. gives hierarchical layer of features | mildly anatomical. analyzable w/ information theory & statistical mechanics | ||
| Weakness | hard to train due to lateral connections | equilibrium requires too many iterations | integer & real-valued neurons are more complicated. |
Hebbian Learning, ART, SOM
The classical example of unsupervised learning in the study of neural networks is Donald Hebb's principle, that is, neurons that fire together wire together.[6] In Hebbian learning, the connection is reinforced irrespective of an error, but is exclusively a function of the coincidence between action potentials between the two neurons.[7] A similar version that modifies synaptic weights takes into account the time between the action potentials (spike-timing-dependent plasticity or STDP). Hebbian Learning has been hypothesized to underlie a range of cognitive functions, such as pattern recognition and experiential learning.
Among neural network models, the self-organizing map (SOM) and adaptive resonance theory (ART) are commonly used in unsupervised learning algorithms. The SOM is a topographic organization in which nearby locations in the map represent inputs with similar properties. The ART model allows the number of clusters to vary with problem size and lets the user control the degree of similarity between members of the same clusters by means of a user-defined constant called the vigilance parameter. ART networks are used for many pattern recognition tasks, such as automatic target recognition and seismic signal processing.[8]









