Probability distribution
Scaled inverse chi-squared|
Probability density function  |
|
Cumulative distribution function 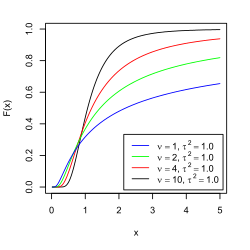 |
| Parameters |

 |
|---|
| Support |
 |
|---|
| PDF |
![{\displaystyle {\frac {(\tau ^{2}\nu /2)^{\nu /2)){\Gamma (\nu /2)))~{\frac {\exp \left[{\frac {-\nu \tau ^{2)){2x))\right]}{x^{1+\nu /2))))](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0745f89b0b5a5ae479cba30f5cbe929d5dfe6c4) |
|---|
| CDF |
 |
|---|
| Mean |
 for for  |
|---|
| Mode |
 |
|---|
| Variance |
 for for  |
|---|
| Skewness |
 for for  |
|---|
| Excess kurtosis |
 for for  |
|---|
| Entropy |

 |
|---|
| MGF |
 |
|---|
| CF |
 |
|---|
The scaled inverse chi-squared distribution  , where
, where  is the scale parameter, equals the univariate inverse Wishart distribution
is the scale parameter, equals the univariate inverse Wishart distribution
 with degrees of freedom
with degrees of freedom  .
.
This family of scaled inverse chi-squared distributions is linked to the inverse-chi-squared distribution and to the chi-squared distribution:
If  then
then  as well as
as well as  and
and  .
.
Instead of  , the scaled inverse chi-squared distribution is however most frequently
parametrized by the scale parameter
, the scaled inverse chi-squared distribution is however most frequently
parametrized by the scale parameter  and the distribution
and the distribution  is denoted by
is denoted by  .
.
In terms of  the above relations can be written as follows:
the above relations can be written as follows:
If  then
then  as well as
as well as  and
and  .
.
This family of scaled inverse chi-squared distributions is a reparametrization of the inverse-gamma distribution.
Specifically, if
 then
then 
Either form may be used to represent the maximum entropy distribution for a fixed first inverse moment  and first logarithmic moment
and first logarithmic moment  .
.
The scaled inverse chi-squared distribution also has a particular use in Bayesian statistics. Specifically, the scaled inverse chi-squared distribution can be used as a conjugate prior for the variance parameter of a normal distribution.
The same prior in alternative parametrization is given by
the inverse-gamma distribution.
Characterization
The probability density function of the scaled inverse chi-squared distribution extends over the domain  and is
and is
![{\displaystyle f(x;\nu ,\tau ^{2})={\frac {(\tau ^{2}\nu /2)^{\nu /2)){\Gamma (\nu /2)))~{\frac {\exp \left[{\frac {-\nu \tau ^{2)){2x))\right]}{x^{1+\nu /2))))](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1bf27f69f750f896de47bdcd485b9ecba90b361)
where  is the degrees of freedom parameter and
is the degrees of freedom parameter and  is the scale parameter. The cumulative distribution function is
is the scale parameter. The cumulative distribution function is


where  is the incomplete gamma function,
is the incomplete gamma function,  is the gamma function and
is the gamma function and  is a regularized gamma function. The characteristic function is
is a regularized gamma function. The characteristic function is


where  is the modified Bessel function of the second kind.
is the modified Bessel function of the second kind.
Bayesian estimation of the variance of a normal distribution
The scaled inverse chi-squared distribution has a second important application, in the Bayesian estimation of the variance of a Normal distribution.
According to Bayes' theorem, the posterior probability distribution for quantities of interest is proportional to the product of a prior distribution for the quantities and a likelihood function:

where D represents the data and I represents any initial information about σ2 that we may already have.
The simplest scenario arises if the mean μ is already known; or, alternatively, if it is the conditional distribution of σ2 that is sought, for a particular assumed value of μ.
Then the likelihood term L(σ2|D) = p(D|σ2) has the familiar form
![{\displaystyle {\mathcal {L))(\sigma ^{2}|D,\mu )={\frac {1}{\left({\sqrt {2\pi ))\sigma \right)^{n))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4943ac8fdd3af8089ce64ae432297094ee8b0bc2)
Combining this with the rescaling-invariant prior p(σ2|I) = 1/σ2, which can be argued (e.g. following Jeffreys) to be the least informative possible prior for σ2 in this problem, gives a combined posterior probability
![{\displaystyle p(\sigma ^{2}|D,I,\mu )\propto {\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2f59d780af470614405f6ff518ebca3b00aede4)
This form can be recognised as that of a scaled inverse chi-squared distribution, with parameters ν = n and τ2 = s2 = (1/n) Σ (xi-μ)2
Gelman et al remark that the re-appearance of this distribution, previously seen in a sampling context, may seem remarkable; but given the choice of prior the "result is not surprising".[1]
In particular, the choice of a rescaling-invariant prior for σ2 has the result that the probability for the ratio of σ2 / s2 has the same form (independent of the conditioning variable) when conditioned on s2 as when conditioned on σ2:

In the sampling-theory case, conditioned on σ2, the probability distribution for (1/s2) is a scaled inverse chi-squared distribution; and so the probability distribution for σ2 conditioned on s2, given a scale-agnostic prior, is also a scaled inverse chi-squared distribution.
Use as an informative prior
If more is known about the possible values of σ2, a distribution from the scaled inverse chi-squared family, such as Scale-inv-χ2(n0, s02) can be a convenient form to represent a more informative prior for σ2, as if from the result of n0 previous observations (though n0 need not necessarily be a whole number):
![{\displaystyle p(\sigma ^{2}|I^{\prime },\mu )\propto {\frac {1}{\sigma ^{n_{0}+2))}\;\exp \left[-{\frac {n_{0}s_{0}^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd531671f3b283268de8d05dab1a5b22315e5328)
Such a prior would lead to the posterior distribution
![{\displaystyle p(\sigma ^{2}|D,I^{\prime },\mu )\propto {\frac {1}{\sigma ^{n+n_{0}+2))}\;\exp \left[-{\frac {ns^{2}+n_{0}s_{0}^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50d412a06cd622273c7353e2e1ff9d7a01376f64)
which is itself a scaled inverse chi-squared distribution. The scaled inverse chi-squared distributions are thus a convenient conjugate prior family for σ2 estimation.
Estimation of variance when mean is unknown
If the mean is not known, the most uninformative prior that can be taken for it is arguably the translation-invariant prior p(μ|I) ∝ const., which gives the following joint posterior distribution for μ and σ2,
![{\displaystyle {\begin{aligned}p(\mu ,\sigma ^{2}\mid D,I)&\propto {\frac {1}{\sigma ^{n+2))}\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]\\&={\frac {1}{\sigma ^{n+2))}\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\exp \left[-{\frac {n(\mu -{\bar {x)))^{2)){2\sigma ^{2))}\right]\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c192479aa55c83f05982b775313f9d430eb78272)
The marginal posterior distribution for σ2 is obtained from the joint posterior distribution by integrating out over μ,
![{\displaystyle {\begin{aligned}p(\sigma ^{2}|D,I)\;\propto \;&{\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\;\int _{-\infty }^{\infty }\exp \left[-{\frac {n(\mu -{\bar {x)))^{2)){2\sigma ^{2))}\right]d\mu \\=\;&{\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\;{\sqrt {2\pi \sigma ^{2}/n))\\\propto \;&(\sigma ^{2})^{-(n+1)/2}\;\exp \left[-{\frac {(n-1)s^{2)){2\sigma ^{2))}\right]\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7abc48680dfd62bf653242c81857f3d9c0d7d4d2)
This is again a scaled inverse chi-squared distribution, with parameters  and
and  .
.





![{\displaystyle {\frac {(\tau ^{2}\nu /2)^{\nu /2)){\Gamma (\nu /2)))~{\frac {\exp \left[{\frac {-\nu \tau ^{2)){2x))\right]}{x^{1+\nu /2))))](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0745f89b0b5a5ae479cba30f5cbe929d5dfe6c4)



































![{\displaystyle f(x;\nu ,\tau ^{2})={\frac {(\tau ^{2}\nu /2)^{\nu /2)){\Gamma (\nu /2)))~{\frac {\exp \left[{\frac {-\nu \tau ^{2)){2x))\right]}{x^{1+\nu /2))))](https://wikimedia.org/api/rest_v1/media/math/render/svg/e1bf27f69f750f896de47bdcd485b9ecba90b361)
















![{\displaystyle {\mathcal {L))(\sigma ^{2}|D,\mu )={\frac {1}{\left({\sqrt {2\pi ))\sigma \right)^{n))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4943ac8fdd3af8089ce64ae432297094ee8b0bc2)
![{\displaystyle p(\sigma ^{2}|D,I,\mu )\propto {\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c2f59d780af470614405f6ff518ebca3b00aede4)

![{\displaystyle p(\sigma ^{2}|I^{\prime },\mu )\propto {\frac {1}{\sigma ^{n_{0}+2))}\;\exp \left[-{\frac {n_{0}s_{0}^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd531671f3b283268de8d05dab1a5b22315e5328)
![{\displaystyle p(\sigma ^{2}|D,I^{\prime },\mu )\propto {\frac {1}{\sigma ^{n+n_{0}+2))}\;\exp \left[-{\frac {ns^{2}+n_{0}s_{0}^{2)){2\sigma ^{2))}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50d412a06cd622273c7353e2e1ff9d7a01376f64)
![{\displaystyle {\begin{aligned}p(\mu ,\sigma ^{2}\mid D,I)&\propto {\frac {1}{\sigma ^{n+2))}\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-\mu )^{2)){2\sigma ^{2))}\right]\\&={\frac {1}{\sigma ^{n+2))}\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\exp \left[-{\frac {n(\mu -{\bar {x)))^{2)){2\sigma ^{2))}\right]\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c192479aa55c83f05982b775313f9d430eb78272)
![{\displaystyle {\begin{aligned}p(\sigma ^{2}|D,I)\;\propto \;&{\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\;\int _{-\infty }^{\infty }\exp \left[-{\frac {n(\mu -{\bar {x)))^{2)){2\sigma ^{2))}\right]d\mu \\=\;&{\frac {1}{\sigma ^{n+2))}\;\exp \left[-{\frac {\sum _{i}^{n}(x_{i}-{\bar {x)))^{2)){2\sigma ^{2))}\right]\;{\sqrt {2\pi \sigma ^{2}/n))\\\propto \;&(\sigma ^{2})^{-(n+1)/2}\;\exp \left[-{\frac {(n-1)s^{2)){2\sigma ^{2))}\right]\end{aligned))}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7abc48680dfd62bf653242c81857f3d9c0d7d4d2)






