Burr Type XII

Probability density function
Cumulative distribution function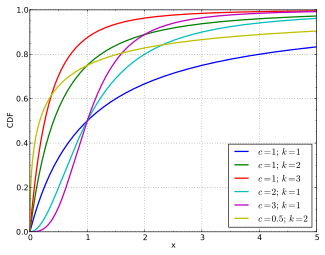
Parameters	${\displaystyle c>0\!}$ ${\displaystyle k>0\!}$
Support	${\displaystyle x>0\!}$
PDF	${\displaystyle ck{\frac {x^{c-1)){(1+x^{c})^{k+1))}\!}$
CDF	${\displaystyle 1-\left(1+x^{c}\right)^{-k))$
Mean	${\displaystyle \mu _{1}=k\operatorname {\mathrm {B} } (k-1/c,\,1+1/c)}$ where Β() is the beta function
Median	${\displaystyle \left(2^{\frac {1}{k))-1\right)^{\frac {1}{c))}$
Mode	${\displaystyle \left({\frac {c-1}{kc+1))\right)^{\frac {1}{c))}$
Variance	${\displaystyle -\mu _{1}^{2}+\mu _{2))$
Skewness	${\displaystyle {\frac {2\mu _{1}^{3}-3\mu _{1}\mu _{2}+\mu _{3)){\left(-\mu _{1}^{2}+\mu _{2}\right)^{3/2))))$
Ex. kurtosis	${\displaystyle {\frac {-3\mu _{1}^{4}+6\mu _{1}^{2}\mu _{2}-4\mu _{1}\mu _{3}+\mu _{4)){\left(-\mu _{1}^{2}+\mu _{2}\right)^{2))}-3}$ where moments (see) ${\displaystyle \mu _{r}=k\operatorname {\mathrm {B} } \left({\frac {ck-r}{c)),\,{\frac {c+r}{c))\right)}$
CF	${\displaystyle ={\frac {c(-it)^{kc)){\Gamma (k)))H_{1,2}^{2,1}\!\left[(-it)^{c}\left|{\begin{matrix}(-k,1)\\(0,1),(-kc,c)\end{matrix))\right.\right],t\neq 0}$ ${\displaystyle =1,t=0}$ where ${\displaystyle \Gamma }$ is the Gamma function and ${\displaystyle H}$ is the Fox H-function.[1]

In probability theory, statistics and econometrics, the Burr Type XII distribution or simply the Burr distribution^[2] is a continuous probability distribution for a non-negative random variable. It is also known as the Singh–Maddala distribution^[3] and is one of a number of different distributions sometimes called the "generalized log-logistic distribution".

Definitions

Probability density function

The Burr (Type XII) distribution has probability density function:^[4][5]

${\displaystyle {\begin{aligned}f(x;c,k)&=ck{\frac {x^{c-1)){(1+x^{c})^{k+1))}\\[6pt]f(x;c,k,\lambda )&={\frac {ck}{\lambda ))\left({\frac {x}{\lambda ))\right)^{c-1}\left[1+\left({\frac {x}{\lambda ))\right)^{c}\right]^{-k-1}\end{aligned))}$

The ${\displaystyle \lambda }$ parameter scales the underlying variate and is a positive real.

Cumulative distribution function

The cumulative distribution function is:

${\displaystyle F(x;c,k)=1-\left(1+x^{c}\right)^{-k))$

${\displaystyle F(x;c,k,\lambda )=1-\left[1+\left({\frac {x}{\lambda ))\right)^{c}\right]^{-k))$

Applications

It is most commonly used to model household income, see for example: Household income in the U.S. and compare to magenta graph at right.

Random variate generation

Given a random variable ${\displaystyle U}$ drawn from the uniform distribution in the interval ${\displaystyle \left(0,1\right)}$, the random variable

${\displaystyle X=\lambda \left({\frac {1}{\sqrt[{k}]{1-U))}-1\right)^{1/c))$

has a Burr Type XII distribution with parameters ${\displaystyle c}$,${\displaystyle k}$ and ${\displaystyle \lambda }$. This follows from the inverse cumulative distribution function given above.

Related distributions

• When c = 1, the Burr distribution becomes the Pareto Type II (Lomax) distribution.

• When k = 1, the Burr distribution is a log-logistic distribution sometimes referred to as the Fisk distribution, a special case of the Champernowne distribution.^[6][7]

• The Burr Type XII distribution is a member of a system of continuous distributions introduced by Irving W. Burr (1942), which comprises 12 distributions.^[8]

• The Dagum distribution, also known as the inverse Burr distribution, is the distribution of 1 / X, where X has the Burr distribution