Generalized Pareto distribution

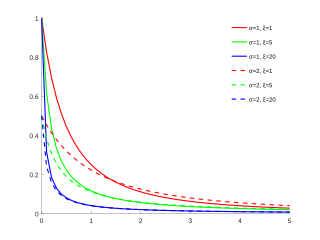
Probability density function GPD distribution functions for ${\displaystyle \mu =0}$ and different values of ${\displaystyle \sigma }$ and ${\displaystyle \xi }$
Cumulative distribution function
Parameters	${\displaystyle \mu \in (-\infty ,\infty )\,}$ location (real) ${\displaystyle \sigma \in (0,\infty )\,}$ scale (real) ${\displaystyle \xi \in (-\infty ,\infty )\,}$ shape (real)
Support	${\displaystyle x\geqslant \mu \,\;(\xi \geqslant 0)}$ ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi \,\;(\xi <0)}$
PDF	${\displaystyle {\frac {1}{\sigma ))(1+\xi z)^{-(1/\xi +1)))$ where ${\displaystyle z={\frac {x-\mu }{\sigma ))}$
CDF	${\displaystyle 1-(1+\xi z)^{-1/\xi }\,}$
Mean	${\displaystyle \mu +{\frac {\sigma }{1-\xi ))\,\;(\xi <1)}$
Median	${\displaystyle \mu +{\frac {\sigma (2^{\xi }-1)}{\xi ))}$
Mode	${\displaystyle \mu }$
Variance	${\displaystyle {\frac {\sigma ^{2)){(1-\xi )^{2}(1-2\xi )))\,\;(\xi <1/2)}$
Skewness	${\displaystyle {\frac {2(1+\xi ){\sqrt {1-2\xi ))}{(1-3\xi )))\,\;(\xi <1/3)}$
Ex. kurtosis	${\displaystyle {\frac {3(1-2\xi )(2\xi ^{2}+\xi +3)}{(1-3\xi )(1-4\xi )))-3\,\;(\xi <1/4)}$
Entropy	${\displaystyle \log(\sigma )+\xi +1}$
MGF	${\displaystyle e^{\theta \mu }\,\sum _{j=0}^{\infty }\left[{\frac {(\theta \sigma )^{j)){\prod _{k=0}^{j}(1-k\xi )))\right],\;(k\xi <1)}$
CF	${\displaystyle e^{it\mu }\,\sum _{j=0}^{\infty }\left[{\frac {(it\sigma )^{j)){\prod _{k=0}^{j}(1-k\xi )))\right],\;(k\xi <1)}$
Method of Moments	${\displaystyle \xi ={\frac {1}{2))\left(1-{\frac {(E[X]-\mu )^{2)){V[X]))\right)}$ ${\displaystyle \sigma =(E[X]-\mu )(1-\xi )}$
CVaR (ES)	${\displaystyle {\begin{cases}\mu +\sigma \left[{\frac {(1-p)^{-\xi )){1-\xi ))+{\frac {(1-p)^{-\xi }-1}{\xi ))\right]&,\xi \neq 0\\\mu +\sigma [1-\ln(1-p)]&,\xi =0\end{cases))}$[1]
bPOE	${\displaystyle {\begin{cases}{\frac {\left(1+{\frac {\xi (x-\mu )}{\sigma ))\right)^{-{\frac {1}{\xi )))){(1-\xi )^{\frac {1}{\xi ))))&,\xi \neq 0\\\ e^{1-\left({\frac {x-\mu }{\sigma ))\right)}&,\xi =0\end{cases))}$[1]

In statistics, the generalized Pareto distribution (GPD) is a family of continuous probability distributions. It is often used to model the tails of another distribution. It is specified by three parameters: location ${\displaystyle \mu }$, scale ${\displaystyle \sigma }$, and shape ${\displaystyle \xi }$.^[2][3] Sometimes it is specified by only scale and shape^[4] and sometimes only by its shape parameter. Some references give the shape parameter as ${\displaystyle \kappa =-\xi \,}$.^[5]

Definition

The standard cumulative distribution function (cdf) of the GPD is defined by^[6]

${\displaystyle F_{\xi }(z)={\begin{cases}1-\left(1+\xi z\right)^{-1/\xi }&{\text{for ))\xi \neq 0,\\1-e^{-z}&{\text{for ))\xi =0.\end{cases))}$

where the support is ${\displaystyle z\geq 0}$ for ${\displaystyle \xi \geq 0}$ and ${\displaystyle 0\leq z\leq -1/\xi }$ for ${\displaystyle \xi <0}$. The corresponding probability density function (pdf) is

${\displaystyle f_{\xi }(z)={\begin{cases}(1+\xi z)^{-{\frac {\xi +1}{\xi ))}&{\text{for ))\xi \neq 0,\\e^{-z}&{\text{for ))\xi =0.\end{cases))}$

Characterization

The related location-scale family of distributions is obtained by replacing the argument z by ${\displaystyle {\frac {x-\mu }{\sigma ))}$ and adjusting the support accordingly.

The cumulative distribution function of ${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$ (${\displaystyle \mu \in \mathbb {R} }$, ${\displaystyle \sigma >0}$, and ${\displaystyle \xi \in \mathbb {R} }$) is

${\displaystyle F_{(\mu ,\sigma ,\xi )}(x)={\begin{cases}1-\left(1+{\frac {\xi (x-\mu )}{\sigma ))\right)^{-1/\xi }&{\text{for ))\xi \neq 0,\\1-\exp \left(-{\frac {x-\mu }{\sigma ))\right)&{\text{for ))\xi =0,\end{cases))}$

where the support of ${\displaystyle X}$ is ${\displaystyle x\geqslant \mu }$ when ${\displaystyle \xi \geqslant 0\,}$, and ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ when ${\displaystyle \xi <0}$.

The probability density function (pdf) of ${\displaystyle X\sim GPD(\mu ,\sigma ,\xi )}$ is

${\displaystyle f_{(\mu ,\sigma ,\xi )}(x)={\frac {1}{\sigma ))\left(1+{\frac {\xi (x-\mu )}{\sigma ))\right)^{\left(-{\frac {1}{\xi ))-1\right)))$,

again, for ${\displaystyle x\geqslant \mu }$ when ${\displaystyle \xi \geqslant 0}$, and ${\displaystyle \mu \leqslant x\leqslant \mu -\sigma /\xi }$ when ${\displaystyle \xi <0}$.

The pdf is a solution of the following differential equation:^{[citation needed]}

${\displaystyle \left\((\begin{array}{l}f'(x)(-\mu \xi +\sigma +\xi x)+(\xi +1)f(x)=0,\\f(0)={\frac {\left(1-{\frac {\mu \xi }{\sigma ))\right)^{-{\frac {1}{\xi ))-1)){\sigma ))\end{array))\right\))$

Special cases

• If the shape ${\displaystyle \xi }$ and location ${\displaystyle \mu }$ are both zero, the GPD is equivalent to the exponential distribution.
• With shape ${\displaystyle \xi =-1}$, the GPD is equivalent to the continuous uniform distribution ${\displaystyle U(0,\sigma )}$.^[7]
• With shape ${\displaystyle \xi >0}$ and location ${\displaystyle \mu =\sigma /\xi }$, the GPD is equivalent to the Pareto distribution with scale ${\displaystyle x_{m}=\sigma /\xi }$ and shape ${\displaystyle \alpha =1/\xi }$.
• If ${\displaystyle X}$ ${\displaystyle \sim }$ ${\displaystyle GPD}$ ${\displaystyle (}$${\displaystyle \mu =0}$, ${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$, then ${\displaystyle Y=\log(X)\sim exGPD(\sigma ,\xi )}$ [1]. (exGPD stands for the exponentiated generalized Pareto distribution.)
• GPD is similar to the Burr distribution.

Generating generalized Pareto random variables

Generating GPD random variables

If U is uniformly distributed on (0, 1], then

${\displaystyle X=\mu +{\frac {\sigma (U^{-\xi }-1)}{\xi ))\sim GPD(\mu ,\sigma ,\xi \neq 0)}$

and

${\displaystyle X=\mu -\sigma \ln(U)\sim GPD(\mu ,\sigma ,\xi =0).}$

Both formulas are obtained by inversion of the cdf.

In Matlab Statistics Toolbox, you can easily use "gprnd" command to generate generalized Pareto random numbers.

GPD as an Exponential-Gamma Mixture

A GPD random variable can also be expressed as an exponential random variable, with a Gamma distributed rate parameter.

${\displaystyle X|\Lambda \sim \operatorname {Exp} (\Lambda )}$

and

${\displaystyle \Lambda \sim \operatorname {Gamma} (\alpha ,\beta )}$

then

${\displaystyle X\sim \operatorname {GPD} (\xi =1/\alpha ,\ \sigma =\beta /\alpha )}$

Notice however, that since the parameters for the Gamma distribution must be greater than zero, we obtain the additional restrictions that:${\displaystyle \xi }$ must be positive.

Exponentiated generalized Pareto distribution

The exponentiated generalized Pareto distribution (exGPD)

The pdf of the ${\displaystyle exGPD(\sigma ,\xi )}$ (exponentiated generalized Pareto distribution) for different values ${\displaystyle \sigma }$ and ${\displaystyle \xi }$.

If ${\displaystyle X\sim GPD}$ ${\displaystyle (}$${\displaystyle \mu =0}$, ${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$, then ${\displaystyle Y=\log(X)}$ is distributed according to the exponentiated generalized Pareto distribution, denoted by ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$.

The probability density function(pdf) of ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )\,\,(\sigma >0)}$ is

${\displaystyle g_{(\sigma ,\xi )}(y)={\begin{cases}{\frac {e^{y)){\sigma )){\bigg (}1+{\frac {\xi e^{y)){\sigma )){\bigg )}^{-1/\xi -1}\,\,\,\,{\text{for ))\xi \neq 0,\\{\frac {1}{\sigma ))e^{y-e^{y}/\sigma }\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi =0,\end{cases))}$

where the support is ${\displaystyle -\infty <y<\infty }$ for ${\displaystyle \xi \geq 0}$, and ${\displaystyle -\infty <y\leq \log(-\sigma /\xi )}$ for ${\displaystyle \xi <0}$.

For all ${\displaystyle \xi }$, the ${\displaystyle \log \sigma }$ becomes the location parameter. See the right panel for the pdf when the shape ${\displaystyle \xi }$ is positive.

The exGPD has finite moments of all orders for all ${\displaystyle \sigma >0}$ and ${\displaystyle -\infty <\xi <\infty }$.

The variance of the ${\displaystyle exGPD(\sigma ,\xi )}$ as a function of ${\displaystyle \xi }$. Note that the variance only depends on ${\displaystyle \xi }$. The red dotted line represents the variance evaluated at ${\displaystyle \xi =0}$, that is, ${\displaystyle \psi '(1)=\pi ^{2}/6}$.

The moment-generating function of ${\displaystyle Y\sim exGPD(\sigma ,\xi )}$ is

${\displaystyle M_{Y}(s)=E[e^{sY}]={\begin{cases}-{\frac {1}{\xi )){\bigg (}-{\frac {\sigma }{\xi )){\bigg )}^{s}B(s+1,-1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))s\in (-1,\infty ),\xi <0,\\{\frac {1}{\xi )){\bigg (}{\frac {\sigma }{\xi )){\bigg )}^{s}B(s+1,1/\xi -s)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))s\in (-1,1/\xi ),\xi >0,\\\sigma ^{s}\Gamma (1+s)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))s\in (-1,\infty ),\xi =0,\end{cases))}$

where ${\displaystyle B(a,b)}$ and ${\displaystyle \Gamma (a)}$ denote the beta function and gamma function, respectively.

The expected value of ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$ depends on the scale ${\displaystyle \sigma }$ and shape ${\displaystyle \xi }$ parameters, while the ${\displaystyle \xi }$ participates through the digamma function:

${\displaystyle E[Y]={\begin{cases}\log \ {\bigg (}-{\frac {\sigma }{\xi )){\bigg )}+\psi (1)-\psi (-1/\xi +1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi <0,\\\log \ {\bigg (}{\frac {\sigma }{\xi )){\bigg )}+\psi (1)-\psi (1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi >0,\\\log \sigma +\psi (1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi =0.\end{cases))}$

Note that for a fixed value for the ${\displaystyle \xi \in (-\infty ,\infty )}$, the ${\displaystyle \log \ \sigma }$ plays as the location parameter under the exponentiated generalized Pareto distribution.

The variance of ${\displaystyle Y}$ ${\displaystyle \sim }$ ${\displaystyle exGPD}$ ${\displaystyle (}$${\displaystyle \sigma }$, ${\displaystyle \xi }$ ${\displaystyle )}$ depends on the shape parameter ${\displaystyle \xi }$ only through the polygamma function of order 1 (also called the trigamma function):

${\displaystyle Var[Y]={\begin{cases}\psi '(1)-\psi '(-1/\xi +1)\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi <0,\\\psi '(1)+\psi '(1/\xi )\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi >0,\\\psi '(1)\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,{\text{for ))\xi =0.\end{cases))}$

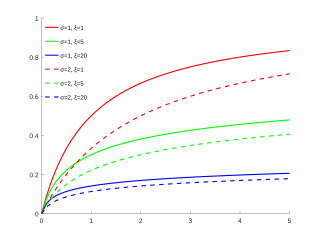
See the right panel for the variance as a function of ${\displaystyle \xi }$. Note that ${\displaystyle \psi '(1)=\pi ^{2}/6\approx 1.644934}$.

Note that the roles of the scale parameter ${\displaystyle \sigma }$ and the shape parameter ${\displaystyle \xi }$ under ${\displaystyle Y\sim exGPD(\sigma ,\xi )}$ are separably interpretable, which may lead to a robust efficient estimation for the ${\displaystyle \xi }$ than using the ${\displaystyle X\sim GPD(\sigma ,\xi )}$ [2]. The roles of the two parameters are associated each other under ${\displaystyle X\sim GPD(\mu =0,\sigma ,\xi )}$ (at least up to the second central moment); see the formula of variance ${\displaystyle Var(X)}$ wherein both parameters are participated.

The Hill's estimator

Assume that ${\displaystyle X_{1:n}=(X_{1},\cdots ,X_{n})}$ are ${\displaystyle n}$ observations (not need to be i.i.d.) from an unknown heavy-tailed distribution ${\displaystyle F}$ such that its tail distribution is regularly varying with the tail-index ${\displaystyle 1/\xi }$ (hence, the corresponding shape parameter is ${\displaystyle \xi }$). To be specific, the tail distribution is described as

${\displaystyle {\bar {F))(x)=1-F(x)=L(x)\cdot x^{-1/\xi },\,\,\,\,\,{\text{for some ))\xi >0,\,\,{\text{where ))L{\text{ is a slowly varying function.))}$

It is of a particular interest in the extreme value theory to estimate the shape parameter ${\displaystyle \xi }$, especially when ${\displaystyle \xi }$ is positive (so called the heavy-tailed distribution).

Let ${\displaystyle F_{u))$ be their conditional excess distribution function. Pickands–Balkema–de Haan theorem (Pickands, 1975; Balkema and de Haan, 1974) states that for a large class of underlying distribution functions ${\displaystyle F}$, and large ${\displaystyle u}$, ${\displaystyle F_{u))$ is well approximated by the generalized Pareto distribution (GPD), which motivated Peak Over Threshold (POT) methods to estimate ${\displaystyle \xi }$: the GPD plays the key role in POT approach.

A renowned estimator using the POT methodology is the Hill's estimator. Technical formulation of the Hill's estimator is as follows. For ${\displaystyle 1\leq i\leq n}$, write ${\displaystyle X_{(i)))$ for the ${\displaystyle i}$-th largest value of ${\displaystyle X_{1},\cdots ,X_{n))$. Then, with this notation, the Hill's estimator (see page 190 of Reference 5 by Embrechts et al [3]) based on the ${\displaystyle k}$ upper order statistics is defined as

${\displaystyle {\widehat {\xi ))_{k}^{\text{Hill))={\widehat {\xi ))_{k}^{\text{Hill))(X_{1:n})={\frac {1}{k-1))\sum _{j=1}^{k-1}\log {\bigg (}{\frac {X_{(j))){X_{(k)))}{\bigg )},\,\,\,\,\,\,\,\,{\text{for ))2\leq k\leq n.}$

In practice, the Hill estimator is used as follows. First, calculate the estimator ${\displaystyle {\widehat {\xi ))_{k}^{\text{Hill))}$ at each integer ${\displaystyle k\in \{2,\cdots ,n\))$, and then plot the ordered pairs ${\displaystyle \{(k,{\widehat {\xi ))_{k}^{\text{Hill)))\}_{k=2}^{n))$. Then, select from the set of Hill estimators ${\displaystyle \((\widehat {\xi ))_{k}^{\text{Hill))\}_{k=2}^{n))$ which are roughly constant with respect to ${\displaystyle k}$: these stable values are regarded as reasonable estimates for the shape parameter ${\displaystyle \xi }$. If ${\displaystyle X_{1},\cdots ,X_{n))$ are i.i.d., then the Hill's estimator is a consistent estimator for the shape parameter ${\displaystyle \xi }$ [4].

Note that the Hill estimator ${\displaystyle {\widehat {\xi ))_{k}^{\text{Hill))}$ makes a use of the log-transformation for the observations ${\displaystyle X_{1:n}=(X_{1},\cdots ,X_{n})}$. (The Pickand's estimator ${\displaystyle {\widehat {\xi ))_{k}^{\text{Pickand))}$ also employed the log-transformation, but in a slightly different way [5].)