Weibull (2-parameter)

Probability density function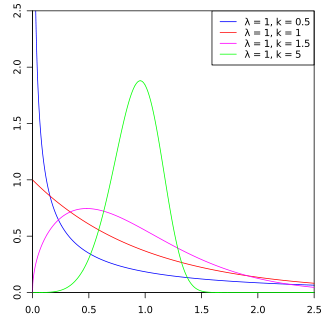
Cumulative distribution function
Parameters	${\displaystyle \lambda \in (0,+\infty )\,}$ scale ${\displaystyle k\in (0,+\infty )\,}$ shape
Support	${\displaystyle x\in [0,+\infty )\,}$
PDF	${\displaystyle f(x)={\begin{cases}{\frac {k}{\lambda ))\left({\frac {x}{\lambda ))\right)^{k-1}e^{-(x/\lambda )^{k)),&x\geq 0,\\0,&x<0.\end{cases))}$
CDF	${\displaystyle {\begin{cases}1-e^{-(x/\lambda )^{k)),&x\geq 0,\\0,&x<0.\end{cases))}$
Mean	${\displaystyle \lambda \,\Gamma (1+1/k)\,}$
Median	${\displaystyle \lambda (\ln 2)^{1/k}\,}$
Mode	${\displaystyle {\begin{cases}\lambda \left({\frac {k-1}{k))\right)^{1/k}\,,&k>1,\\0,&k\leq 1.\end{cases))}$
Variance	${\displaystyle \lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k))\right)-\left(\Gamma \left(1+{\frac {1}{k))\right)\right)^{2}\right]\,}$
Skewness	${\displaystyle {\frac {\Gamma (1+3/k)\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3)){\sigma ^{3))))$
Ex. kurtosis	(see text)
Entropy	${\displaystyle \gamma (1-1/k)+\ln(\lambda /k)+1\,}$
MGF	${\displaystyle \sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n)){n!))\Gamma (1+n/k),\ k\geq 1}$
CF	${\displaystyle \sum _{n=0}^{\infty }{\frac {(it)^{n}\lambda ^{n)){n!))\Gamma (1+n/k)}$
Kullback-Leibler divergence	see below
CVaR (ES)	${\displaystyle {\frac {\lambda }{1-p))\Gamma _{U}\left(1+{\frac {1}{k)),-\ln(1-p)\right)}$ where ${\displaystyle \Gamma _{U}(a,b)=\int _{b}^{\infty }p^{a-1}e^{-p}dp}$ is the upper incomplete gamma function.[1]

In probability theory and statistics, the Weibull distribution /ˈwaɪbʊl/ is a continuous probability distribution. It models a broad range of random variables, largely in the nature of a time to failure or time between events. Examples are maximum one-day rainfalls and the time a user spends on a web page.

The distribution is named after Swedish mathematician Waloddi Weibull, who described it in detail in 1951, although it was first identified by Maurice René Fréchet and first applied by Rosin & Rammler (1933) to describe a particle size distribution.

Definition

Standard parameterization

The probability density function of a Weibull random variable is^[2][3]

${\displaystyle f(x;\lambda ,k)={\begin{cases}{\frac {k}{\lambda ))\left({\frac {x}{\lambda ))\right)^{k-1}e^{-(x/\lambda )^{k)),&x\geq 0,\\0,&x<0,\end{cases))}$

where k > 0 is the shape parameter and λ > 0 is the scale parameter of the distribution. Its complementary cumulative distribution function is a stretched exponential function. The Weibull distribution is related to a number of other probability distributions; in particular, it interpolates between the exponential distribution (k = 1) and the Rayleigh distribution (k = 2 and ${\displaystyle \lambda ={\sqrt {2))\sigma }$^[4]).

If the quantity X is a "time-to-failure", the Weibull distribution gives a distribution for which the failure rate is proportional to a power of time. The shape parameter, k, is that power plus one, and so this parameter can be interpreted directly as follows:^[5]

• A value of ${\displaystyle k<1\,}$ indicates that the failure rate decreases over time (like in case of the Lindy effect, which however corresponds to Pareto distributions^[6] rather than Weibull distributions). This happens if there is significant "infant mortality", or defective items failing early and the failure rate decreasing over time as the defective items are weeded out of the population. In the context of the diffusion of innovations, this means negative word of mouth: the hazard function is a monotonically decreasing function of the proportion of adopters;
• A value of ${\displaystyle k=1\,}$ indicates that the failure rate is constant over time. This might suggest random external events are causing mortality, or failure. The Weibull distribution reduces to an exponential distribution;
• A value of ${\displaystyle k>1\,}$ indicates that the failure rate increases with time. This happens if there is an "aging" process, or parts that are more likely to fail as time goes on. In the context of the diffusion of innovations, this means positive word of mouth: the hazard function is a monotonically increasing function of the proportion of adopters. The function is first convex, then concave with an inflexion point at ${\displaystyle (e^{1/k}-1)/e^{1/k},\,k>1\,}$.

In the field of materials science, the shape parameter k of a distribution of strengths is known as the Weibull modulus. In the context of diffusion of innovations, the Weibull distribution is a "pure" imitation/rejection model.

Alternative parameterizations

First alternative

Applications in medical statistics and econometrics often adopt a different parameterization.^[7][8] The shape parameter k is the same as above, while the scale parameter is ${\displaystyle b=\lambda ^{-k))$. In this case, for x ≥ 0, the probability density function is

${\displaystyle f(x;k,b)=bkx^{k-1}e^{-bx^{k)),}$

the cumulative distribution function is

${\displaystyle F(x;k,b)=1-e^{-bx^{k)),}$

the hazard function is

${\displaystyle h(x;k,b)=bkx^{k-1},}$

and the mean is

${\displaystyle b^{-1/k}\Gamma (1+1/k).}$

Second alternative

A second alternative parameterization can also be found.^[9][10] The shape parameter k is the same as in the standard case, while the scale parameter λ is replaced with a rate parameter β = 1/λ. Then, for x ≥ 0, the probability density function is

${\displaystyle f(x;k,\beta )=\beta k({\beta x})^{k-1}e^{-(\beta x)^{k))}$

the cumulative distribution function is

${\displaystyle F(x;k,\beta )=1-e^{-(\beta x)^{k)),}$

and the hazard function is

${\displaystyle h(x;k,\beta )=\beta k({\beta x})^{k-1}.}$

In all three parameterizations, the hazard is decreasing for k < 1, increasing for k > 1 and constant for k = 1, in which case the Weibull distribution reduces to an exponential distribution.

Properties

Density function

The form of the density function of the Weibull distribution changes drastically with the value of k. For 0 < k < 1, the density function tends to ∞ as x approaches zero from above and is strictly decreasing. For k = 1, the density function tends to 1/λ as x approaches zero from above and is strictly decreasing. For k > 1, the density function tends to zero as x approaches zero from above, increases until its mode and decreases after it. The density function has infinite negative slope at x = 0 if 0 < k < 1, infinite positive slope at x = 0 if 1 < k < 2 and null slope at x = 0 if k > 2. For k = 1 the density has a finite negative slope at x = 0. For k = 2 the density has a finite positive slope at x = 0. As k goes to infinity, the Weibull distribution converges to a Dirac delta distribution centered at x = λ. Moreover, the skewness and coefficient of variation depend only on the shape parameter. A generalization of the Weibull distribution is the hyperbolastic distribution of type III.

Cumulative distribution function

The cumulative distribution function for the Weibull distribution is

${\displaystyle F(x;k,\lambda )=1-e^{-(x/\lambda )^{k))\,}$

for x ≥ 0, and F(x; k; λ) = 0 for x < 0.

If x = λ then F(x; k; λ) = 1 − e⁻¹ ≈ 0.632 for all values of k. Vice versa: at F(x; k; λ) = 0.632 the value of x ≈ λ.

The quantile (inverse cumulative distribution) function for the Weibull distribution is

${\displaystyle Q(p;k,\lambda )=\lambda (-\ln(1-p))^{1/k))$

for 0 ≤ p < 1.

The failure rate h (or hazard function) is given by

${\displaystyle h(x;k,\lambda )={k \over \lambda }\left({x \over \lambda }\right)^{k-1}.}$

The Mean time between failures MTBF is

${\displaystyle {\text{MTBF))(k,\lambda )=\lambda \Gamma (1+1/k).}$

Moments

The moment generating function of the logarithm of a Weibull distributed random variable is given by^[11]

${\displaystyle \operatorname {E} \left[e^{t\log X}\right]=\lambda ^{t}\Gamma \left({\frac {t}{k))+1\right)}$

where Γ is the gamma function. Similarly, the characteristic function of log X is given by

${\displaystyle \operatorname {E} \left[e^{it\log X}\right]=\lambda ^{it}\Gamma \left({\frac {it}{k))+1\right).}$

In particular, the nth raw moment of X is given by

${\displaystyle m_{n}=\lambda ^{n}\Gamma \left(1+{\frac {n}{k))\right).}$

The mean and variance of a Weibull random variable can be expressed as

${\displaystyle \operatorname {E} (X)=\lambda \Gamma \left(1+{\frac {1}{k))\right)\,}$

and

${\displaystyle \operatorname {var} (X)=\lambda ^{2}\left[\Gamma \left(1+{\frac {2}{k))\right)-\left(\Gamma \left(1+{\frac {1}{k))\right)\right)^{2}\right]\,.}$

The skewness is given by

${\displaystyle \gamma _{1}={\frac {2\Gamma _{1}^{3}-3\Gamma _{1}\Gamma _{2}+\Gamma _{3)){[\Gamma _{2}-\Gamma _{1}^{2}]^{3/2))))$

where ${\displaystyle \Gamma _{i}=\Gamma (1+i/k)}$, which may also be written as

${\displaystyle \gamma _{1}={\frac {\Gamma \left(1+{\frac {3}{k))\right)\lambda ^{3}-3\mu \sigma ^{2}-\mu ^{3)){\sigma ^{3))))$

where the mean is denoted by μ and the standard deviation is denoted by σ.

The excess kurtosis is given by

${\displaystyle \gamma _{2}={\frac {-6\Gamma _{1}^{4}+12\Gamma _{1}^{2}\Gamma _{2}-3\Gamma _{2}^{2}-4\Gamma _{1}\Gamma _{3}+\Gamma _{4)){[\Gamma _{2}-\Gamma _{1}^{2}]^{2))))$

where ${\displaystyle \Gamma _{i}=\Gamma (1+i/k)}$. The kurtosis excess may also be written as:

${\displaystyle \gamma _{2}={\frac {\lambda ^{4}\Gamma (1+{\frac {4}{k)))-4\gamma _{1}\sigma ^{3}\mu -6\mu ^{2}\sigma ^{2}-\mu ^{4)){\sigma ^{4))}-3.}$

Moment generating function

A variety of expressions are available for the moment generating function of X itself. As a power series, since the raw moments are already known, one has

${\displaystyle \operatorname {E} \left[e^{tX}\right]=\sum _{n=0}^{\infty }{\frac {t^{n}\lambda ^{n)){n!))\Gamma \left(1+{\frac {n}{k))\right).}$

Alternatively, one can attempt to deal directly with the integral

${\displaystyle \operatorname {E} \left[e^{tX}\right]=\int _{0}^{\infty }e^{tx}{\frac {k}{\lambda ))\left({\frac {x}{\lambda ))\right)^{k-1}e^{-(x/\lambda )^{k))\,dx.}$

If the parameter k is assumed to be a rational number, expressed as k = p/q where p and q are integers, then this integral can be evaluated analytically.^[12] With t replaced by −t, one finds

${\displaystyle \operatorname {E} \left[e^{-tX}\right]={\frac {1}{\lambda ^{k}\,t^{k))}\,{\frac {p^{k}\,{\sqrt {q/p))}{({\sqrt {2\pi )))^{q+p-2))}\,G_{p,q}^{\,q,p}\!\left(\left.{\begin{matrix}{\frac {1-k}{p)),{\frac {2-k}{p)),\dots ,{\frac {p-k}{p))\\{\frac {0}{q)),{\frac {1}{q)),\dots ,{\frac {q-1}{q))\end{matrix))\;\right|\,{\frac {p^{p)){\left(q\,\lambda ^{k}\,t^{k}\right)^{q))}\right)}$

where G is the Meijer G-function.

The characteristic function has also been obtained by Muraleedharan et al. (2007). The characteristic function and moment generating function of 3-parameter Weibull distribution have also been derived by Muraleedharan & Soares (2014) harvtxt error: no target: CITEREFMuraleedharanSoares2014 (help) by a direct approach.

Reparametrization tricks

Fix some ${\displaystyle \alpha >0}$. Let ${\displaystyle (\pi _{1},...,\pi _{n})}$ be nonnegative, and not all zero, and let ${\displaystyle g_{1},...,g_{n))$ be independent samples of ${\displaystyle {\text{Weibull))(1,\alpha ^{-1})}$, then^[13]

• ${\displaystyle \arg \min _{i}(g_{i}\pi _{i}^{-\alpha })\sim {\text{Categorical))\left({\frac {\pi _{j)){\sum _{i}\pi _{i))}\right)_{j))$
• ${\displaystyle \min _{i}(g_{i}\pi _{i}^{-\alpha })\sim {\text{Weibull))\left(\left(\sum _{i}\pi _{i}\right)^{-\alpha },\alpha ^{-1}\right)}$.

Shannon entropy

The information entropy is given by

${\displaystyle H(\lambda ,k)=\gamma \left(1-{\frac {1}{k))\right)+\ln \left({\frac {\lambda }{k))\right)+1}$

where ${\displaystyle \gamma }$ is the Euler–Mascheroni constant. The Weibull distribution is the maximum entropy distribution for a non-negative real random variate with a fixed expected value of x^k equal to λ^k and a fixed expected value of ln(x^k) equal to ln(λ^k) − ${\displaystyle \gamma }$.

Parameter estimation

Maximum likelihood

The maximum likelihood estimator for the ${\displaystyle \lambda }$ parameter given ${\displaystyle k}$ is

${\displaystyle {\widehat {\lambda ))=({\frac {1}{n))\sum _{i=1}^{n}x_{i}^{k})^{\frac {1}{k))}$

The maximum likelihood estimator for ${\displaystyle k}$ is the solution for k of the following equation^[14]

${\displaystyle 0={\frac {\sum _{i=1}^{n}x_{i}^{k}\ln x_{i)){\sum _{i=1}^{n}x_{i}^{k))}-{\frac {1}{k))-{\frac {1}{n))\sum _{i=1}^{n}\ln x_{i))$

This equation defining ${\displaystyle {\widehat {k))}$ only implicitly, one must generally solve for ${\displaystyle k}$ by numerical means.

When ${\displaystyle x_{1}>x_{2}>\cdots >x_{N))$ are the ${\displaystyle N}$ largest observed samples from a dataset of more than ${\displaystyle N}$ samples, then the maximum likelihood estimator for the ${\displaystyle \lambda }$ parameter given ${\displaystyle k}$ is^[14]

${\displaystyle {\widehat {\lambda ))^{k}={\frac {1}{N))\sum _{i=1}^{N}(x_{i}^{k}-x_{N}^{k})}$

Also given that condition, the maximum likelihood estimator for ${\displaystyle k}$ is^{[citation needed]}

${\displaystyle 0={\frac {\sum _{i=1}^{N}(x_{i}^{k}\ln x_{i}-x_{N}^{k}\ln x_{N})}{\sum _{i=1}^{N}(x_{i}^{k}-x_{N}^{k})))-{\frac {1}{N))\sum _{i=1}^{N}\ln x_{i))$

Again, this being an implicit function, one must generally solve for ${\displaystyle k}$ by numerical means.

Kullback–Leibler divergence

The Kullback–Leibler divergence between two Weibulll distributions is given by^[15]

${\displaystyle D_{\text{KL))(\mathrm {Weib} _{1}\parallel \mathrm {Weib} _{2})=\log {\frac {k_{1)){\lambda _{1}^{k_{1))))-\log {\frac {k_{2)){\lambda _{2}^{k_{2))))+(k_{1}-k_{2})\left[\log \lambda _{1}-{\frac {\gamma }{k_{1))}\right]+\left({\frac {\lambda _{1)){\lambda _{2))}\right)^{k_{2))\Gamma \left({\frac {k_{2)){k_{1))}+1\right)-1}$

Weibull plot

Weibull plot

The fit of a Weibull distribution to data can be visually assessed using a Weibull plot.^[16] The Weibull plot is a plot of the empirical cumulative distribution function ${\displaystyle {\widehat {F))(x)}$ of data on special axes in a type of Q–Q plot. The axes are ${\displaystyle \ln(-\ln(1-{\widehat {F))(x)))}$ versus ${\displaystyle \ln(x)}$. The reason for this change of variables is the cumulative distribution function can be linearized:

${\displaystyle {\begin{aligned}F(x)&=1-e^{-(x/\lambda )^{k))\\[4pt]-\ln(1-F(x))&=(x/\lambda )^{k}\\[4pt]\underbrace {\ln(-\ln(1-F(x)))} _{\textrm {'y'))&=\underbrace {k\ln x} _{\textrm {'mx'))-\underbrace {k\ln \lambda } _{\textrm {'c'))\end{aligned))}$

which can be seen to be in the standard form of a straight line. Therefore, if the data came from a Weibull distribution then a straight line is expected on a Weibull plot.

There are various approaches to obtaining the empirical distribution function from data: one method is to obtain the vertical coordinate for each point using ${\displaystyle {\widehat {F))={\frac {i-0.3}{n+0.4))}$ where ${\displaystyle i}$ is the rank of the data point and ${\displaystyle n}$ is the number of data points.^[17]

Linear regression can also be used to numerically assess goodness of fit and estimate the parameters of the Weibull distribution. The gradient informs one directly about the shape parameter ${\displaystyle k}$ and the scale parameter ${\displaystyle \lambda }$ can also be inferred.

Applications

The Weibull distribution is used^{[citation needed]}

Fitted cumulative Weibull distribution to maximum one-day rainfalls using CumFreq, see also distribution fitting^[18]

Fitted curves for oil production time series data ^[19]

• In survival analysis
• In reliability engineering and failure analysis
• In electrical engineering to represent overvoltage occurring in an electrical system
• In industrial engineering to represent manufacturing and delivery times
• In extreme value theory
• In weather forecasting and the wind power industry to describe wind speed distributions, as the natural distribution often matches the Weibull shape^[20]
• In communications systems engineering
  • In radar systems to model the dispersion of the received signals level produced by some types of clutters
  • To model fading channels in wireless communications, as the Weibull fading model seems to exhibit good fit to experimental fading channel measurements
• In information retrieval to model dwell times on web pages.^[21]
• In general insurance to model the size of reinsurance claims, and the cumulative development of asbestosis losses
• In forecasting technological change (also known as the Sharif-Islam model)^[22]
• In hydrology the Weibull distribution is applied to extreme events such as annual maximum one-day rainfalls and river discharges.
• In decline curve analysis to model oil production rate curve of shale oil wells.^[19]
• In describing the size of particles generated by grinding, milling and crushing operations, the 2-Parameter Weibull distribution is used, and in these applications it is sometimes known as the Rosin–Rammler distribution.^[23] In this context it predicts fewer fine particles than the log-normal distribution and it is generally most accurate for narrow particle size distributions.^[24] The interpretation of the cumulative distribution function is that ${\displaystyle F(x;k,\lambda )}$ is the mass fraction of particles with diameter smaller than ${\displaystyle x}$, where ${\displaystyle \lambda }$ is the mean particle size and ${\displaystyle k}$ is a measure of the spread of particle sizes.
• In describing random point clouds (such as the positions of particles in an ideal gas): the probability to find the nearest-neighbor particle at a distance ${\displaystyle x}$ from a given particle is given by a Weibull distribution with ${\displaystyle k=3}$ and ${\displaystyle \rho =1/\lambda ^{3))$ equal to the density of the particles.^[25]
• In calculating the rate of radiation-induced single event effects onboard spacecraft, a four-parameter Weibull distribution is used to fit experimentally measured device cross section probability data to a particle linear energy transfer spectrum.^[26] The Weibull fit was originally used because of a belief that particle energy levels align to a statistical distribution, but this belief was later proven false and the Weibull fit continues to be used because of its many adjustable parameters, rather than a demonstrated physical basis.^[27]

Related distributions

• A Weibull distribution is a generalized gamma distribution with both shape parameters equal to k.
• The translated Weibull distribution (or 3-parameter Weibull) contains an additional parameter.^[11] It has the probability density function

  ${\displaystyle f(x;k,\lambda ,\theta )={k \over \lambda }\left({x-\theta \over \lambda }\right)^{k-1}e^{-\left({x-\theta \over \lambda }\right)^{k))\,}$

  for ${\displaystyle x\geq \theta }$ and ${\displaystyle f(x;k,\lambda ,\theta )=0}$ for ${\displaystyle x<\theta }$, where ${\displaystyle k>0}$ is the shape parameter, ${\displaystyle \lambda >0}$ is the scale parameter and ${\displaystyle \theta }$ is the location parameter of the distribution. ${\displaystyle \theta }$ value sets an initial failure-free time before the regular Weibull process begins. When ${\displaystyle \theta =0}$, this reduces to the 2-parameter distribution.
• The Weibull distribution can be characterized as the distribution of a random variable ${\displaystyle W}$ such that the random variable

  ${\displaystyle X=\left({\frac {W}{\lambda ))\right)^{k))$

  is the standard exponential distribution with intensity 1.^[11]
• This implies that the Weibull distribution can also be characterized in terms of a uniform distribution: if ${\displaystyle U}$ is uniformly distributed on ${\displaystyle (0,1)}$, then the random variable ${\displaystyle W=\lambda (-\ln(U))^{1/k}\,}$ is Weibull distributed with parameters ${\displaystyle k}$ and ${\displaystyle \lambda }$. Note that ${\displaystyle -\ln(U)}$ here is equivalent to ${\displaystyle X}$ just above. This leads to an easily implemented numerical scheme for simulating a Weibull distribution.
• The Weibull distribution interpolates between the exponential distribution with intensity ${\displaystyle 1/\lambda }$ when ${\displaystyle k=1}$ and a Rayleigh distribution of mode ${\displaystyle \sigma =\lambda /{\sqrt {2))}$ when ${\displaystyle k=2}$.
• The Weibull distribution (usually sufficient in reliability engineering) is a special case of the three parameter exponentiated Weibull distribution where the additional exponent equals 1. The exponentiated Weibull distribution accommodates unimodal, bathtub shaped^[28] and monotone failure rates.
• The Weibull distribution is a special case of the generalized extreme value distribution. It was in this connection that the distribution was first identified by Maurice Fréchet in 1927.^[29] The closely related Fréchet distribution, named for this work, has the probability density function

  ${\displaystyle f_{\rm {Frechet))(x;k,\lambda )={\frac {k}{\lambda ))\left({\frac {x}{\lambda ))\right)^{-1-k}e^{-(x/\lambda )^{-k))=f_{\rm {Weibull))(x;-k,\lambda ).}$

• The distribution of a random variable that is defined as the minimum of several random variables, each having a different Weibull distribution, is a poly-Weibull distribution.
• The Weibull distribution was first applied by Rosin & Rammler (1933) to describe particle size distributions. It is widely used in mineral processing to describe particle size distributions in comminution processes. In this context the cumulative distribution is given by

  ${\displaystyle f(x;P_{\rm {80)),m)={\begin{cases}1-e^{\ln \left(0.2\right)\left({\frac {x}{P_{\rm {80))))\right)^{m))&x\geq 0,\\0&x<0,\end{cases))}$

  where
  • ${\displaystyle x}$ is the particle size
  • ${\displaystyle P_{\rm {80))}$ is the 80th percentile of the particle size distribution
  • ${\displaystyle m}$ is a parameter describing the spread of the distribution
• Because of its availability in spreadsheets, it is also used where the underlying behavior is actually better modeled by an Erlang distribution.^[30]
• If ${\displaystyle X\sim \mathrm {Weibull} (\lambda ,{\frac {1}{2)))}$ then ${\displaystyle {\sqrt {X))\sim \mathrm {Exponential} ({\frac {1}{\sqrt {\lambda ))})}$ (Exponential distribution)
• For the same values of k, the Gamma distribution takes on similar shapes, but the Weibull distribution is more platykurtic.

• From the viewpoint of the Stable count distribution, ${\displaystyle k}$ can be regarded as Lévy's stability parameter. A Weibull distribution can be decomposed to an integral of kernel density where the kernel is either a Laplace distribution ${\displaystyle F(x;1,\lambda )}$ or a Rayleigh distribution ${\displaystyle F(x;2,\lambda )}$:

  ${\displaystyle F(x;k,\lambda )={\begin{cases}\displaystyle \int _{0}^{\infty }{\frac {1}{\nu ))\,F(x;1,\lambda \nu )\left(\Gamma \left({\frac {1}{k))+1\right){\mathfrak {N))_{k}(\nu )\right)\,d\nu ,&1\geq k>0;{\text{or ))\\\displaystyle \int _{0}^{\infty }{\frac {1}{s))\,F(x;2,{\sqrt {2))\lambda s)\left({\sqrt {\frac {2}{\pi ))}\,\Gamma \left({\frac {1}{k))+1\right)V_{k}(s)\right)\,ds,&2\geq k>0;\end{cases))}$

  where ${\displaystyle {\mathfrak {N))_{k}(\nu )}$ is the Stable count distribution and ${\displaystyle V_{k}(s)}$ is the Stable vol distribution.