
Decompression in the context of diving derives from the reduction in ambient pressure experienced by the diver during the ascent at the end of a dive or hyperbaric exposure and refers to both the reduction in pressure and the process of allowing dissolved inert gases to be eliminated from the tissues during this reduction in pressure.
When a diver descends in the water column the ambient pressure rises. Breathing gas is supplied at the same pressure as the surrounding water, and some of this gas dissolves into the diver's blood and other tissues. Inert gas continues to be taken up until the gas dissolved in the diver is in a state of equilibrium with the breathing gas in the diver's lungs, (see: "Saturation diving"), or the diver moves up in the water column and reduces the ambient pressure of the breathing gas until the inert gases dissolved in the tissues are at a higher concentration than the equilibrium state, and start diffusing out again. Dissolved inert gases such as nitrogen or helium can form bubbles in the blood and tissues of the diver if the partial pressures of the dissolved gases in the diver get too high when compared to the ambient pressure. These bubbles, and products of injury caused by the bubbles, can cause damage to tissues generally known as decompression sickness or the bends. The immediate goal of controlled decompression is to avoid development of symptoms of bubble formation in the tissues of the diver, and the long-term goal is to also avoid complications due to sub-clinical decompression injury.
The symptoms of decompression sickness are known to be caused by damage resulting from the formation and growth of bubbles of inert gas within the tissues and by blockage of arterial blood supply to tissues by gas bubbles and other emboli consequential to bubble formation and tissue damage. The precise mechanisms of bubble formation and the damage they cause has been the subject of medical research for a considerable time and several hypotheses have been advanced and tested. Tables and algorithms for predicting the outcome of decompression schedules for specified hyperbaric exposures have been proposed, tested, and used, and usually found to be of some use but not entirely reliable. Decompression remains a procedure with some risk, but this has been reduced and is generally considered to be acceptable for dives within the well-tested range of commercial, military and recreational diving.
The first recorded experimental work related to decompression was conducted by Robert Boyle, who subjected experimental animals to reduced ambient pressure by use of a primitive vacuum pump. In the earliest experiments the subjects died from asphyxiation, but in later experiments, signs of what was later to become known as decompression sickness were observed. Later, when technological advances allowed the use of pressurisation of mines and caissons to exclude water ingress, miners were observed to present symptoms of what would become known as caisson disease, the bends, and decompression sickness. Once it was recognized that the symptoms were caused by gas bubbles, and that recompression could relieve the symptoms, further work showed that it was possible to avoid symptoms by slow decompression, and subsequently various theoretical models have been derived to predict low-risk decompression profiles and treatment of decompression sickness.
Timeline
[edit]

- 1660 – Sir Robert Boyle conducted an experiment on a bird in an air pump. This predated actual intentional investigations into decompression, but the experiment was effectively a rapid decompression and caused the death of the bird by asphyxiation.[1]
- 1670 – Sir Robert Boyle performed an experiment with a viper in a vacuum. A bubble was observed in its eye and it displayed signs of extreme discomfort. This was the first recorded description of decompression sickness.[2]
- 1841 – Jacques Triger documented the first cases of decompression sickness in humans when two miners involved in pressurised caisson work developed symptoms.[2]
- 1847 – The effectiveness of recompression for the treatment of decompression sickness (DCS) in caisson workers was described by B. Pol and T.J. Watelle.[2][3]
- 1857 – Felix Hoppe-Seyler repeated Boyle's experiments and suggested that sudden death in compressed air workers was caused by bubble formation, and recommended recompression therapy.[4]
- 1861 - Bucquoy proposed the hypothesis that "les gaz du sang... repassent à l'état libre sous l'influence de la décompression ...et occasionnent des accidents comparables à ceux d'une injection d'air dans les veines" ("the blood gases ... return to the free state under the influence of decompression ... and cause accidents comparable to those of an injection of air in the veins").[5]
- 1868 – Alfred Le Roy de Méricourt described decompression sickness as an occupational illness of sponge divers.[3]
- 1873 – Dr. Andrew Smith first used the terms "caisson disease" and "compressed air illness", describing 110 cases of decompression sickness as the physician in charge during construction of the Brooklyn Bridge.[4][6] The nickname "the bends" was used after workers emerging from pressurized construction on the Brooklyn Bridge adopted a posture similar to fashionable ladies of the period "the Grecian Bend".[2]
- 1878 – Paul Bert determined that decompression sickness is caused by nitrogen gas bubbles released from tissues and blood during or after decompression, and showed the advantages of breathing oxygen after developing decompression sickness.[7]
- 1889–90 - Ernest William Moir builds the first medical airlock when he noticed that about 25% of the workforce digging the Hudson River Tunnel were dying from decompression sickness and realised that the solution was recompression.[8][9]
- 1897 – N. Zuntz proposed a perfusion-based tissue model.[10]
- 1906 – V. Schrotter suggested a uniform decompression of 20 minutes per atmosphere of pressure. J.S. Haldane was commissioned by the British Admiralty to study decompression sickness.[4]
- 1908 – John Scott Haldane prepared the first recognised decompression table for the British Admiralty.[11] This table was based on experiments performed on goats using an end point of symptomatic DCS.[2][11]
- 1912 – Chief Gunner George D. Stillson of the United States Navy created a program to test and refine Haldane's tables.[12] This program ultimately led to the first publication of the United States Navy Diving Manual and the establishment of a Navy Diving School in Newport, Rhode Island. Diver training programs were later cut at the end of World War I.
- 1912 – Leonard Erskine Hill proposed continuous uniform decompression[2][3]
- 1915 - US Navy published C&R tables.[13]
- 1916 - UN Navy established its Deep Sea Diving School in Newport, Rhode Island.[13]
- 1924 - US Navy published first US Navy Diving Manual.[13]
- 1927 – Naval School, Diving and Salvage was re-established at the Washington Navy Yard. At that time the United States moved their Navy Experimental Diving Unit (NEDU) to the same naval yard. In the following years, the Experimental Diving Unit developed the US Navy Air Decompression Tables which became the accepted world standard for diving with compressed air.[14]
- 1930's – J.A. Hawkins, C.W. Schilling and R.A. Hansen conducted extensive experimental dives to determine allowable supersaturation ratios for different tissue compartments for Haldanean model.[15]
- 1935 – Albert R. Behnke et al. experimented with oxygen for recompression therapy.[2]
- 1937 – US Navy 1937 tables developed by O.D. Yarborough were published.[15]
- 1941 – Altitude decompression sickness was treated with hyperbaric oxygen for the first time.[16]
- 1942 – Aggazzotti and Ligabue detect evidence that gas particles in the free state exist in living animal tissue.[17][18]
- 1956 – US Navy Decompression Tables developed by M. Des Granges (1956) were published.[19]
- 1960 – F.C. Golding et al. split the classification of DCS into Type 1 and 2.[20]
- 1965 – LeMessurier and Hills published their paper, A thermodynamic approach arising from a study on Torres Strait diving techniques, which suggested that decompression by conventional models results in bubble formation which is then eliminated by re-dissolving at the decompression stops which is slower than off-gassing while still in solution. This indicates the importance of minimizing bubble phase for efficient gas elimination.[21][22]
- 1965 – French Navy GERS (Groupe d'Etudes et Recherches Sous-marines) 1965 table was published.[5]
- 1965 – M.W. Goodman and Robert D. Workman introduced recompression (treatment) tables utilizing oxygen to accelerate elimination of inert gas[23][24]
- 1965 – US Navy publishes Nitrox and Heliox tables developed by Robert D. Workman.[25]
- 1971 – Albano proposed a method for decompression based on the assumption that tissue microbubble growth could be controlled by ensuring that a maximum supersaturation in tissues is not exceeded.[18][26]
- 1971 – In the US, the Williams-Steiger Occupational Safety and Health Act of 1970 triggered investigation of the safety of US Navy tables in reaction to an attempt to legislate their use for commercial diving.[18]
- 1972 – Royal Naval Physiological Laboratory (RNPL) published tables based on Hempleman's tissue slab diffusion model.[27]
- 1973 – Isobaric counterdiffusion was first described by D.J. Graves, J. Idicula, Christian Lambertson, and J.A. Quinn in subjects who breathed one inert gas mixture while being surrounded by another.[28][29]
- 1973 – French civilian Tables du Ministère du Travail 1974 (MT74) were published.[30]
- 1976 – M.P. Spencer showed that the sensitivity of decompression testing is increased by the use of ultrasonic methods which can detect mobile venous bubbles before symptoms of DCS emerge.[31]
- 1976 – Edward Beckman published findings of a comparison of US Navy air tables with RNPL, Buhlmann and other tables and indicating that the US Navy tables for diving below 100 fsw which were reputed to produce unacceptable rates of decompression sickness for civilian applications, were significantly less conservative than the other models in the comparison.[18]
- 1981 – Huggins model and tables using Spencer's formula for no-decompression limits were published.[32]
- 1981 – D.E. Yount described the Varied Permeability Model.[33]
- 1982 – Paul K Weathersby, Louis D Homer and Edward T Flynn introduced survival analysis into the study of decompression sickness.[34]
- 1983 – E.D. Thalmann published the E-L model for constant PO2 nitrox and heliox closed circuit rebreathers.[35]
- 1983/4 – Albert A. Bühlmann published Decompression–Decompression sickness.[36] Bühlmann recognized the problems associated with altitude diving and proposed a method which calculated maximum nitrogen loading in the tissues at a particular ambient pressure. Set of parameters : ZH-L 12.
- 1984 – DCIEM (Defence and Civil Institution of Environmental Medicine, Canada) released No-Decompression and Decompression Tables based on Kidd/Stubbs serial compartment model and extensive ultrasonic testing.[37]
- 1984 – Edward D. Thalmann published U.S. Navy Exponential-Linear algorithm and tables for constant PO2 Nitrox closed circuit rebreather (CCR) applications.[38]
- 1985 – Thalmann extended use of the E-L model for constant PO2 heliox closed circuit rebreathers.[39]
- 1985 – Bruce Bassett published recreational decompression tables based on U.S. Navy Tables.[40]
- 1986 – Bühlmann's set of parameters air : ZH-L 16 A (experimental), B (tables), C (computers) and heliox.[41]
- 1986 – Swiss Sport Diving Tables based on Bühlmann's set of parameters were published.[32]
- 1986 – D. E. Yount and D. C. Hoffman proposed a bubble model, which was to become the core of the Varying Permeability Model (VPM).[42][43]
- 1988 – Bühlmann's set of parameters air : ZH-L 6 (dive computer Aladin Pro).[44]
- 1988 – BSAC'88 tables were published.[45]
- 1990 – DCIEM sport diving tables released.[37]
- 1990 – French Navy – Marine Nationale 90 (MN90) decompression tables published.[5]
- 1992 – French civilian Tables du Ministère du Travail 1992 (MT92) published.[46]
- 1992 – Bühlmann's set of parameters air : ZH-L 8 ADT (dive computer Aladin Air X - presented in BOOT 1994).[44]
- 1999 – National Association of Underwater Instructors (NAUI) published Trimix and Nitrox tables based on Bruce Wienke's RGBM model.[47]
- 2000 - The core VPM algorithm was finalized.[43]
- 2001 – NAUI published recreational air tables based on the RGBM model.[48]
- 2003 – V-Planner with VPM-B model by Erik Baker was released as a revision to work from the DecoList (1999) participants: Eric Maiken, D.E. Yount and others.[43]
- 2007 –Wayne Gerth & David J. Doolette published VVal 18 and VVal 18M parameter sets for tables and programs based on the Thalmann E-L algorithm, and produced an internally compatible set of decompression tables for open circuit and CCR on air and Nitrox, including in water air/oxygen decompression and surface decompression on oxygen.[49]
- 2007 – Saul Goldman proposed an Interconnected Compartment Model (3 compartment series/parallel model) using a single risk bearing active tissue compartment and two non-risk bearing peripheral compartments which indirectly affect the risk of the central compartment. This model predicts initially fast gas washout which slows with time.[50]
- 2008 – US Navy Diving Manual Revision 6 published, which includes a version of the 2007 tables by Gerth & Doolette.[51]
Haldanean (perfusion limited, dissolved phase) models
[edit]Early decompression theory generally assumed that inert gas bubble formation in the tissues could be avoided during decompression, and the aim of the decompression tables and algorithms was to prevent bubble formation while minimising decompression time. Most dissolved phase models are perfusion limited, and differ mainly by the number of compartments, the range of half-times, and supersaturation tolerances assumed. These models are commonly referred to as Haldanean.[52]
Haldane's theory and tables
[edit]John Scott Haldane was commissioned by the Royal Navy to develop a safe decompression procedure. The current method was a slow linear decompression, and Haldane was concerned that this was ineffective due to additional nitrogen buildup in the slow early stages of the ascent.[53]
Haldane's hypothesis was that a diver could ascend immediately to a depth where the supersaturation reaches but does not exceed the critical supersaturation level, at which depth the pressure gradient for off-gassing is maximized and the decompression is most efficient. The diver would remain at this depth until saturation had reduced sufficiently for him to ascend another 10 feet, to the new depth of critical supersaturation, where the process would be repeated until it was safe for the diver to reach the surface. Haldane assumed a constant critical ratio of dissolved nitrogen pressure to ambient pressure which was invariant with depth.[53]
A large number of decompression experiments were done using goats, which were compressed for three hours to assumed saturation, rapidly decompressed to surface pressure, and examined for symptoms of decompression sickness. Goats which had been compressed to 2.25 bar absolute or less showed no signs of DCS after rapid decompression to the surface. Goats compressed to 6 bar and rapidly decompressed to 2.6 bar (pressure ratio 2.3 to 1) also showed no signs of DCS. Haldane and his co-workers concluded that a decompression from saturation with a pressure ratio of 2 to 1 was unlikely to produce symptoms.[54]
Haldane's model
[edit]The decompression model formulated from these findings made the following assumptions.[11]
- Living tissues become saturated at different rates in different parts of the body. Saturation time varies from a few minutes to several hours
- The rate of saturation follows a logarithmic curve and is approximately complete in 3 hours in goats, and 5 hours in humans.
- The desaturation process follows the same pressure/time function as saturation (symmetrical), provided no bubbles have formed
- The slow tissues are most important in avoiding bubble formation
- A pressure ratio of 2 to 1 during decompression will not produce decompression symptoms
- A supersaturation of dissolved Nitrogen that exceeds twice ambient atmospheric pressure is unsafe
- Efficient decompression from high pressures should start by rapidly halving the absolute pressure, followed by a slower ascent to ensure that the partial pressure in the tissues does not at any stage exceed about twice the ambient pressure.
- The different tissues were designated as tissue groups with different half-times, and saturation was assumed after four half-times (93.75%)
- Five tissue compartments were chosen, with half-times of 5, 10, 20, 40 and 75 minutes.[55]
- Depth intervals of 10 ft were chosen for decompression stops.[11]
Decompression tables
[edit]This model was used to compute a set of tables. The method comprises choosing a depth and time exposure, and calculation the nitrogen partial pressure in each of the tissue compartments at the end of that exposure.[11]
- The depth of the first stop is found from the tissue compartment with the highest partial pressure, and the depth of first decompression stop is the standard stop depth where this partial pressure is nearest without exceeding the critical pressure ratio.[11]
- The time at each stop is the time required to reduce partial pressure in all compartments to a level safe for the next stop, 10 ft shallower.[11]
- The controlling compartment for the first stop is usually the fastest tissue, but this generally changes during the ascent, and slower tissues usually control the shallower stop times. The longer the bottom time and closer to saturation of the slower tissues, the slower the tissue controlling the final stops will be.[11]
Chamber tests and open water dives with two divers were made in 1906. The divers were successfully decompressed from each exposure.[11] The tables were adopted by the Royal Navy in 1908. The Haldane tables of 1906 are considered to be the first true set of decompression tables, and the basic concept of parallel tissue compartments with half-times and critical supersaturation limits are still in use in several later decompression models, algorithms, tables and decompression computers.[56]
U.S. Navy decompression tables
[edit]US Navy decompression tables have gone through a lot of development over the years. They have mostly been based on parallel multi-compartment exponential models. The number of compartments has varied, and the allowable supersaturation in the various compartments during ascent has undergone major development based on experimental work and records of decompression sickness incidents.[57]
C&R tables (1915)
[edit]The first decompression tables produced for the U.S. Navy were developed by the Bureau of Construction and Repair in 1915 and were consequently known as the C&R tables. They were derived from a Haldanean model, with oxygen decompression to depths up to 300 ft on air, and were successfully used to depths of slightly over 300 ft[58]
Hawkins Schilling and Hansen (1930s)
[edit]Submarine escape training led US Navy personnel to believe that Haldane's allowable supersaturation ratios for fast tissues were unnecessarily conservative, as calculated values indicated that supersaturation in trainees exceeded Haldane's limits, but they did not develop DCS. A large number (2143) of experimental dives were conducted over 3 years to derive allowable supersaturation ratios for a Haldanian 5 compartment model with compartment half-times of 5, 10, 20, 40 and 70 minutes. Values for critical supersaturation derived from this experimental work were different for each tissue compartment. Values for slow tissues (75 and 40-minute) were close to Haldane's findings, but considerably higher values were found for the fast tissues. These values were so high that the researchers concluded that the 5- and 10-minute tissues were not relevant to the development of DCS. Based on these conclusions, a set of tables was computed which omitted the 5- and 10-minute tissues.[15]
Yarbrough (1937 tables)
[edit]Yarbrough's 1937 tables were based on a Haldanean 3 compartment model with compartment half-times of 20, 40 and 70 minutes. Ascent rate was chosen to be 25 ft per minute, which was a convenient rate to pull up a diver in standard dress.[15]
1956 tables
[edit]Van der Aue worked on procedures for surface decompression and oxygen use in the early 1950s and during his research found problems with the 1937 tables for long dive times. He also found that the fast tissues which had been dropped in the 1930s would control decompression in some cases, so he re-introduced the fast compartments to the model, and added an extra slower compartment to better model long-duration dives.[59]
Assumptions of the 1956 model:[59]
- Six parallel tissue compartments with exponential uptake and elimination of gas with compartment half-times of 5, 10, 20, 40, 80 and 120 minutes.[59]
- Symmetrical uptake and elimination half-times (same half-time for each compartment for uptake and elimination)[59]
- Supersaturation ratios decrease linearly with increased ambient pressure, (M-values) and are different for each compartment.[59][60]
- Each tissue compartment is assumed to fully saturate/desaturate in 6 half-times. This means desaturation of the slowest (120 min) compartment takes 12 hours – hence the 12-hour surface interval before a dive is not considered repetitive with these tables.[59]
Ascent rate was chosen at 60 fsw/min as a compromise between the practical requirements for military scuba and surface supplied diving operations.[61]
Repetitive diving was accommodated in the tables using the slowest compartment to control surface off-gassing.[62]
A minimum surface interval of 10 minutes was found necessary to ensure that the 120-minute compartment would have controlling effect for repetitive dives.[63]
U.S. Navy exceptional exposure tables
[edit]The U.S. Navy 1956 tables were soon found to be problematic for dives deeper than 100 fsw for longer than 2 to 4 hours.[64]
US Navy exceptional exposure tables use an 8 compartment Haldanean model developed by Workman, with half-times of 5, 10, 20, 40, 80, 120, 160 and 240 minutes, and are not compatible with the rest of the US Navy Air tables for repetitive diving, although for convenience they have been appended to the standard US Navy Air tables.[64] The tables warn that no repetitive diving is permitted following an exceptional exposure dive, and although the 240-minute tissue would only desaturate completely in 24 hours, there is no restriction to assuming an unsaturated diver after 12 hours.[65]
Reformatting of the U.S. Navy 1956 tables by recreational diving community
[edit]Some of the earliest modifications to the U.S. Navy tables involved changes to their layout by the recreational diving community. These include:[66][67]
- Nu-Way repetitive dive tables
- Dacor "No calculation dive tables"
- NAUI tables (original version)
Modified U.S. Navy 1956 tables
[edit]Decompression theory is not an exact science. Decompression models approximate a physiological process that is incompletely understood, and rather complex, by simple mathematical models, in the hope of producing a useful procedure with acceptably low risk of injury to the user. New information allows theories and models to be modified to provide more reliable results, and the availability of faster and more powerful computer processors at low cost has made more exhaustive numerical methods more practicable, and the computation of relatively far more complex models is now quite possible, even in real time.[68]
Several factors have encouraged researchers to modify existing tables and develop new models:
- Doppler bubble detection allows models to use bubble formation as an endpoint rather than symptomatic DCS.[69]
- The use of safety stops has been shown by Dr Andrew Pilmanis of the Catalina Marine Science Centre to greatly reduce bubble formation in divers.[69]
- Many decompression models use a slower ascent rate than the 60 fpm (18 m/min) of the 1956 US Navy tables (The 2008 US Navy tables have reduced ascent rate to 30 fpm (9 m/min)).[51][69]
- Multiple repetitive dives. The US Navy tables were designed for a single repetitive dive, and there were concerns about the safety of extending their use to multiple repetitive dives. As an attempt to address this issue, some tables were modified to reduce the allowable bottom time for repetitive dives.[69]
- Longer nitrogen retention. The addition of longer half-time compartments allows the accumulation of residual nitrogen over longer periods to be accounted for.[69]
Jeppesen tables
[edit]Jeppesen made the simplest modification to the U.S. Navy tables by drawing a new line to reduce no-stop limits on an otherwise unchanged table. Divers were recommended to remain within the modified no-stop limit. If one of the new time limits was not listed on the U.S. Navy table, the next shorter table entry was to be selected.[68]
Bassett tables
[edit]These tables were based on the 1956 US Navy tables and the no-decompression limits recommended by Bruce Bassett.[40]
Changes were also made to the table rules and decompression requirements:[40]
- Ascent rate of 10 m per minute.
- A safety stop of 3 to 5 minutes at 3 to 5 metres is recommended where possible for all dives deeper than 9 m.
- Total dive time is used to calculate repetitive group.
NAUI tables
[edit]The first NAUI tables were based on reformatted but otherwise unmodified US Navy 1956 tables and issued in the early 1980s.[67][70]
The next version was a NAUI modification of the US Navy 1956 tables using the following modifications,[40] and released a few years later.
- No decompression limits have been reduced. In most cases this results in the repetitive group shifting one letter down, but for 50fsw it shifted 2 letters, and for 40 fsw, by three letters.
- A precautionary decompression stop (safety stop) of 3 minutes at 15 fsw is recommended after all dives, but the time spent at the safety stop is not included in the time used to calculate repetitive group.
- A surface interval of at least one hour between repetitive dives is recommended.
- Repetitive dive depths are limited to 100 fsw
- A repetitive dive is defined as occurring within 24 hours of the previous dive (this allows for the slowest tissues to equilibriate with atmospheric partial pressures)
- All required decompression is done at a stop depth of 15 fsw
NAUI adapted the 1995 DCIEM Sports Table for use in all NAUI courses and these were used until they were replaced by RGBM based tables in 2002.[71] (The NAUI recreational air tables based on RGBM model are copyrighted 2001)[48]
NAUI RGBM Trimix and Nitrox tables copyrighted 1999 have also been released.[47]
Pandora tables
[edit]These tables were designed for use on the excavation of the wreck of the Pandora[40]
- Table values at 30 fsw (feet of seawater) and deeper were shortened by 1 to 4 minutes, putting divers into higher repetitive groups sooner.[40]
- Repetitive group selection tables for repetitive dives were modified. The first repetitive dive uses the same repetitive group selection as the U.S. Navy tables but subsequent dives use more conservative tables which place the diver in a higher repetitive group than the Navy tables would for the same profile. This tendency is continued for the third and fourth repetitive dives.[40]
- Safety stops at 3 msw (metres of seawater)(10 fsw) are required for repetitive dives; 3 minutes is required after the second dive, 6 minutes after the third and 9 minutes after the fourth dive.[40]
- Maximum ascent rate was specified as 10 msw/min. (35 fsw/min.).[40]
Huggins model and tables
[edit]In 1981 Karl Huggins modified the US Navy 6 compartment model using M values derived to follow the Spencer no-decompression limits. The tables are exclusively for no-decompression diving and are presented in the same format as the US Navy tables.[32]
A major difference from the US Navy tables is that the repetitive group designators represent nitrogen levels in all tissues, unlike the USN table which represent only the 120-minute compartment. The Huggins repetitive group indicates a percentage of the M0 for the most saturated tissue, and this is intended to make the tables more applicable to multilevel diving procedures.[72]
The Huggins tables have not been officially tested, but are more conservative than the 1956 US Navy tables. They have been calculated from limits which would theoretically produce venous bubbles 10 to 20% of the time.[72]
Recreational Dive Planner, distributed by PADI
[edit]The tables known as the Recreational Dive Planner (RDP) were developed and tested by Raymond Rogers and DSAT (Diving Science And Technology, an affiliate of PADI Inc.) exclusively for no-stop diving. The M values were derived from Spencer's no-stop limits and the repetitive group designators were based on a 60-minute tissue compartment. This combination resulted in more conservative first dives, but less conservative repetitive dives.[73]
The RDP tables were developed for no-stop diving, but recommend a safety stop at 15 fsw for 3 minutes. Emergency decompression for dives which inadvertently exceed the no-stop limit is specified.[73]
The RDP tables are available in two formats:
- A regular table
- An electronic app format
- "The Wheel", which was a circular slide-rule type calculator, and allows depths to be read to 5 fsw intervals, and times to the nearest minute, is no longer available. Its functions are within the electronic format.
The RDP was tested for single day multi-level dives and multi-day dives with multiple dives per day. There were no incidences of symptomatic DCS during testing.[73]
Bühlmann tables
[edit]Professor A.A. Bühlmann of the Laboratory of Hyperbaric medicine of the Medical Clinic of the University of Zurich developed the Swiss tables, more often referred to as Bühlmann tables, in the early 1960s. The model is Haldanian, with 16 tissue compartments with half-times from 2.65 minutes to 635 minutes, each with linearly varying supersaturation limits depending on the tissue and the ambient pressure, and is based on absolute pressures, which simplifies application to altitude diving.[36]
The full set of Swiss Tables consists of tables for four altitude ranges: 0 to 700 m, 701 to 1500 m, 1501 to 2500 m and 2501 to 3500 m. Ascent rate was chosen as 10 m per minute.[36]
No stop limits and decompression schedules tend to be more conservative than the US Navy air tables.[74]
The Swiss tables use the 80-minute tissue compartment for control of repetitive dive calculations, which tends to be less conservative than the US Navy tables for this application.[74]
Modified Bühlmann tables
[edit]Swiss sport diving tables
[edit]In 1986 the Bühlmann model was used to generate dive tables for recreational divers. One set was for altitudes from 0 to 700m above sea level (0 to 2300 ft.) and other for altitudes from 701 to 2,500 m (2,300 to 8,202 ft). The repetitive group designators are based on the 80-minute compartment.[32]
Bühlmann/Hahn tables (German)
[edit]The German tables were developed by Dr. Max Hahn using a derivative of the Bühlmann ZH-L16 model using half-times ranging from 2.65 to 635 minutes. Three sets were published for altitude ranges 0–200 m, 201–700 m, and 701–1,200 m. The repetitive group designators are based on the 80-minute compartment.[32]
Safety factors were added to the depths in the table to take into account depth gauge errors. The depths used for calculations were 2.4% greater than the depths listed in the two lower altitude tables, and 3% + 1 msw greater than the depths listed in the highest altitude table.[32]
French Navy – Marine Nationale 90 (MN90) decompression tables
[edit]The mathematical model used for the development of the MN 90 tables is Haldanian, and was also used for the GERS (Groupe d'Etudes et Recherches Sous-marines) 1965 table.[5]
Haldane's assumptions about the limiting factors for ascent are:
- gas exchange in decompression is symmetrical with compression
- the role of bubbles in the modification of blood-tissue exchange is neglected,
- normal decompression does not produce bubbles: DCS occurs when bubbles appear,
- bubbles appear in a compartment where the ratio of the dissolved gas pressure and ambient hydrostatic pressure reaches a critical value, characterizing the maximum tolerable pressure compartment.
Specific assumptions and conditions for use of the MN90 model and tables are as follows:[5]
- For Scuba dives using air as the breathing gas at sea level, with the diver initially saturated at atmospheric pressure
- 12 parallel tissue compartments with half-times from 5 to 120 minutes, each with its own critical ratio
- The ascent rate used is 15 to 17 metres per minute to the first stop, which is the same as used in the GERS 1965 tables. From the first stop to the surface this is reduced to 6 m/min
- The reference population with respect to physiology is based on 1095 medically fit divers from the French Navy in 1988:
- weight 74 kg plus or minus 8 kg,
- height 175.9 plus or minus 5.7 cm,
- age 32.3 plus or minus 6.1 years.
- Only the 120-minute tissue is used for calculation of residual nitrogen for repetitive dives. Letter groups are used to indicate the residual gas content of the 120-minute tissue. Letter groups are modified according to surface interval. A residual nitrogen time is found from the repetitive group and the repetitive dive depth which is to be added to the planned bottom time.
- Decompression stops are at 3 m intervals
- The tables have been validated by experimental dives and modified where necessary.
- The maximum permitted depth for use of air is 60 m. The data for the decompression depths of 62 m and 65 m are included in the table in case of accidentally exceeding the depth limit of 60 m.
- Only one repetitive dive is allowed as there is no validation data for multiple repetitive dives
- Altitude corrections are available
- The tables can be used for Nitrox by calculating equivalent air depth
- Oxygen may be used to accelerate decompression in-water at depths not exceeding 6 m
- An unusual feature of these tables is a table for reduction of residual nitrogen by breathing pure oxygen on the surface between dives.
Non-Haldanean dissolved phase models
[edit]Royal Naval Physiological Laboratory model
[edit]In the early 1950s, Hempleman developed a diffusion limited model for gas transfer from the capillaries into the tissues (Haldanian model is a perfusion model). The basis for this model is radial diffusion from a capillary into the surrounding tissue, but by assuming closely packed capillaries in a plane the model was developed into a "tissue slab" equivalent to one-dimensional linear bulk diffusion in two directions into the tissues from a central surface.[45]
The 1972 RNPL tables were based on a modified Hempleman tissue slab model and are more conservative than the US Navy tables.[45]
A version of the RNPL tables was used by the British Sub-Aqua Club (BSAC) until the production of the BSAC'88 tables in 1988.[45]
DCIEM model and tables
[edit]In the mid-1960s, the Canadian Defence and Civil Institute of Environmental Medicine developed the Kidd/Stubbs serial decompression model. This differs from Haldanian models which are parallel models and assume that all compartments are exposed to ambient partial pressures and no gas interchange occurs between compartments. A serial model assumes that the diffusion takes place through a series of compartments, and only one is exposed to the ambient partial pressures and is in effect a compartmentalised version of the Hempelman bulk diffusion slab model.[37]
The Kidd/Stubbs model has four serial compartments,[75] each with a half time of approximately 21 minutes. Allowable surfacing supersaturation ratios for the initial two compartments are taken as 1.92 and 1.73, while the gas concentration in the last two compartments is not considered in the computation.
DCIEM has continuously evaluated and modified the model over the years. A revised set of tables was released in 1984, based on thousands of Doppler evaluated dives.[37] The DCIEM 1983 decompression model is a decompression calculation model rather than a physiological model.[75] Modifications were made to the model to get it to fit observed data, as the original model had several observed shortcomings, while retaining the basic model structure so that it could be applied to existing hardware with minimal modifications.
Mixed phase models (dissolved and bubble phases)
[edit]Thermodynamic model
[edit]LeMessurier and Hills published a paper in 1965 on A thermodynamic approach arising from a study on Torres Strait diving techniques which suggests that decompression by conventional models results in bubble formation which is then eliminated by re-dissolving at the decompression stops, which is slower than elimination while still in solution, thus indicating the importance of minimising bubble phase for efficient gas elimination.[21][22]
Tables du Ministère du Travail
[edit]Tables du Ministère du Travail 1974 (MT74)
[edit]The first French official (civilian) air decompression tables were published in 1974 by the Ministère du Travail[30][76]
Tables du Ministère du Travail 1992 (MT92)
[edit]In 1982, the French government funded a research project for the evaluation of the MT74 tables using computer analysis of the dive report database, which indicated that the MT74 tables had limitations for severe exposures.[77] The government then supported a second project to develop and validate new tables.[78] A complete set of air tables, with options of pure oxygen breathing at 6 m (surface supplied), at 12 m (wet bell), surface decompression, split level diving, repetitive diving, etc. was developed in 1983. This early model already implemented the concept of continuous compartment half-times. For the safe ascent criteria, the Arterial Bubble model was not derived mathematically, but an approximation was defined empirically by fitting mathematical expressions to selected exposures from the Comex database. At the time, the best fit was obtained by the expression now called AB Model-1, which was used to compute a set of decompression tables that was evaluated offshore on selected Comex worksites. In 1986, after some minor adjustments, the tables were included in the Comex diving manuals and used as standard procedures. In 1992, the tables were included in the new French diving regulations as the Tables du Ministère du Travail 1992, or MT92 tables.[46]
The arterial bubble decompression model
[edit]The arterial bubble assumption is that the filtering capacity of the lung has a threshold radius of the size of a red blood cell and that sufficiently small decompression bubbles can pass to the arterial side, especially during the initial phase of ascent. Later in the ascent, bubbles grow to a larger size and remain trapped in the lung. This may explain why conventional Doppler measurements have not detected any bubbles in the arterial circulation.[30]
The arterial bubble assumption can introduce variability in the decompression outcome through the lung function. The first variable is individual susceptibility. The filtering capacity of the lung may be assumed to vary between individuals, and for a given individual, from day to day, and may account for the variability between divers on the same profile, and between the same diver on different occasions which have been observed in DCS susceptibility.[79] Basically, a good physiology for diving implies an effective bubble filter. This is a justification for divers who seek top physical fitness for severe decompression exposures.
The second variable is related to dive conditions and speculates an influence of CO2 on the lung filter. Raised levels of CO2 could decrease the lungs' filtration capacity and allow bubbles to pass to the arterial side of the circulation.[clarification needed] Thus, diving situations associated with CO2 retention and hypercapnia would be associated with a higher risk of Type II DCS. This could explain why the following situations, which are all related to high levels of CO2, have been identified as contributing factors to DCS:[30]
- anxiety and stress,
- exhaustion or hyperventilation due to intense activity,
- cold,
- high work of breathing.
The arterial bubble assumption is also consistent with the accidental production of arterial bubbles. One scenario considers a shunt at the heart or lung level that passes bubbles from the venous to the arterial side. A patent foramen ovale (PFO) is thought to only open in certain conditions.[80][81] A PFO conveniently explains neurological accidents after recreational air diving without any procedure violation, but it does not explain vestibular hits in deep diving. Vestibular symptoms can appear very early in the decompression, long before the massive bubble production required to overload the system.
A second scenario considers pressure increases during decompression that reduce bubble diameters. This can allow bubbles trapped in the lung during a normal decompression to suddenly pass through the capillaries and become responsible for Type II DCS symptoms. This could explain the difference in outcomes of in-water decompression versus surface decompression.[82] Data collected in the North Sea have shown that if the overall incidence rate of the two diving methods is about the same, that surface decompression tends to produce ten times more type II DCS than in-water decompression. It is assumed that when the diver ascends to the surface, bubbles are produced that are trapped by the lung capillaries, and on recompression of the diver in the deck chamber, these bubbles are reduced in diameter and pass to the arterial side, later causing neurological symptoms. The same scenario was proposed for type II DCS recorded after sawtooth diving profiles or multiple repetitive dives.
The arterial bubble assumption also provides an explanation for the criticality of the initial ascent phase. Bubbles associated with symptoms are not necessarily generated on site. There is a growth process at the beginning of the ascent that may last for several cycles until the bubbles have reached a critical size when they are either filtered in the lung or stopped at the tissue level. It is postulated that the production of a shower of small arterial bubbles during the first minutes of the initial ascent is a precursor for DCS symptoms.
An attempt was made to turn this scenario into a decompression model.
The arterial bubble model assumptions[30][79]
- A diver breathes a compressed gas mixture that contains inert gas which dissolves in the various tissues during the pressure exposure. When the ascent is initiated, the inert gas is off-loaded as soon as a suitable gradient is created.
- Bubbles are normally produced in the vascular bed and transported by the venous system to heart, then to the lungs.
- The lungs work as a filter and trap the bubbles in the capillaries which have a smaller diameter. Gas transfer into the alveoli eliminates the bubbles.
- The critical issue is the filtering capacity of the lung system. Small bubbles may pass through the lungs into the systemic circulation.
- At the level of the aortic arch, the distribution of blood is likely to carry bubbles to neurological tissue such as the brain or the spinal cord.
- The brain is a fast tissue and might be in supersaturated state in the early phase of decompression. It acts as a gas reservoir and feeds any local bubble which will grow. The bubble may just proceed through the capillaries to the venous side for another cycle, but may be trapped and will then grow in place, causing local restriction of the blood supply and finally ischemia. This may develop into central neurological symptoms.
- Similarly, arterial bubbles may reach the spinal cord and grow on site from local gas and produce spinal neurological symptoms.
- Much later in the decompression, bubbles may reach a significant size and exert a local deformation, particularly in stiffer tissues such as tendons and ligaments, that excites nerve terminations and produces pain.
Derivation of the Arterial Bubble Model
A model based on the Arterial Bubble assumption (Arterial Bubble model version 2, or AB Model 2) was developed for the calculation of decompression tables. This gas phase model uses an equation which can be compared to a classic "M-value" associated with a corrective factor that reduces the permitted gradient for small values of the compartment time constant.
The consequence is the introduction of deeper stops than a classic dissolved phase decompression model.
The explanation of the arterial bubble assumption considers two situations:[83]
- At the beginning of decompression, the arrival of an arterial bubble in a neurological tissue during desaturation is posited as the critical event. Gas exchange occurs between the bubble, the blood, and surrounding tissue. If the bubble radius does not exceed a critical value it will not grow in situ and will eventually leave the site. Bubbles larger than the critical size will block the circulation at that point, causing ischaemia in the affected tissues. The criterion of critical bubble radius is used to develop a strategy for safe rate of ascent to avoid type II neurological symptoms by controlling the balance of gas exchange.
- In later stages of decompression, a bubble that has taken up a large quantity of dissolved gas from the adjacent tissue in a joint is considered the critical event for a type I decompression injury. A bubble reaching a critical volume is assumed to have a mechanical effect on the nerve endings in the vicinity, causing pain in a tendon. The criterion of critical bubble volume is used to control the strategy for safe ascent at this stage of decompression by limiting growth of bubble volume.
The critical volume concept was developed by Hennessy and Hempleman who developed a simple mathematical condition linking the dissolved gas concentration and the safe ambient pressure during the ascent:
- Ptissue ≤ a×Pambient + b
Where Ptissue represents the dissolved gas tension, Pambient, the ambient pressure and a and b are two coefficients. This is a simple linear relationship between dissolved gas and ambient pressure which has the same mathematical form as an M value, where the values for the coefficients are determined experimentally. This suggests that all the Haldanean models using M-values (including the US Navy tables previous to those based on the E-L model, the Bühlmann tables and all the French Navy tables), may be considered expressions of the critical volume criterion, though their authors may have argued for other interpretations.[83]
U.S. Navy E-L algorithm and the 2008 tables
[edit]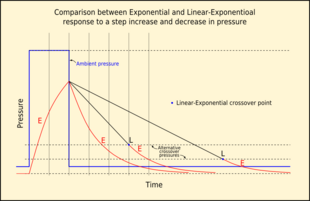
The use of simple symmetrical exponential gas kinetics models has shown up the need for a model that would give slower tissue washout.[84] In the early 1980s the US Navy Experimental Diving Unit developed an algorithm using a decompression model with exponential gas absorption as in the usual Haldanian model, but a slower linear release during ascent. The effect of adding linear kinetics to the exponential model is to lengthen the duration of risk accumulation for a given compartment time constant[84]
The model was originally developed for programming decompression computers for constant oxygen partial pressure closed circuit rebreathers.[85][86] Initial experimental diving using an exponential-exponential algorithm resulted in an unacceptable incidence of DCS, so a change was made to a model using the linear release model, with a reduction in DCS incidence. The same principles were applied to developing an algorithm and tables for a constant oxygen partial pressure model for heliox diving[87]
The linear component is active when the tissue pressure exceeds ambient pressure by a given amount specific to the tissue compartment. When the tissue pressure drops below this cross-over criterion the tissue is modelled by exponential kinetics. During gas uptake, tissue pressure never exceeds ambient, so it is always modelled by exponential kinetics. This results in a model with the desired asymmetrical characteristics of slower washout than uptake.[88] The linear/exponential transition is smooth. Choice of cross-over pressure determines the slope of the linear region as equal to the slope of the exponential region at the cross-over point.
During the development of these algorithms and tables, it was recognized that a successful algorithm could be used to replace the existing collection of incompatible tables for various air and Nitrox diving modes currently in the U.S. Navy Diving Manual with a set of mutually compatible decompression tables based on a single model, which was proposed by Gerth and Doolette in 2007.[89] This has been done in Revision 6 of the US Navy Diving Manual published in 2008, though some changes were made.
An independent implementation of the EL-Real Time Algorithm was developed by Cochran Consulting, Inc. for the diver-carried Navy Dive Computer under the guidance of E. D. Thalmann.[38]
Physiological interpretation
[edit]Computer testing of a theoretical bubble growth model reported by Ball, Himm, Homer and Thalmann produced results which led to the interpretation of the three compartments used in the probabilistic LE model, with fast (1.5 min), intermediate (51 min) and slow (488 min) time constants, of which only the intermediate compartment uses the linear kinetics modification during decompression, as possibly not representing distinct anatomically identifiable tissues, but three different kinetic processes which relate to different elements of DCS risk.[90]
They conclude that bubble evolution may not be sufficient to explain all aspects of DCS risk, and the relationship between gas phase dynamics and tissue injury requires further investigation.[91]
BSAC '88 Tables
[edit]The BSAC '88 Tables are published in the form of a booklet of four table sets giving no calculation repetitive diving solutions from sea level to 3000 metres altitude.[92]
These tables were developed by Tom Hennessy to replace the RNPL/BSAC tables when the Club wanted a set of tables which could approach the versatility of a dive computer.[93]
Very little information on the theoretical model and algorithm for the BSAC 1988 tables appears to be available. What is known, is that the tables were developed specifically for recreational diving for the British Sub-Aqua Club by Dr Tom Hennessy and were released in 1988.[92]
Also in 1988, a chapter titled Modelling Human Exposure to Altered Pressure Environments, by T.R. Hennessy was published in Environmental Ergonomics,[94] discussing the shortcomings of several decompression models and the associated experimental validation procedures. In this work Hennessy proposes an alternative combined perfusion/diffusion model. The number of compartments discussed ranges from 4 in model "A", (perfusion limited aqueous tissue, perfusion limited lipid tissue, diffusion limited aqueous tissue and diffusion limited lipid tissue) to 2 in model "B" (where the assumption is made that if there is intravascular undissolved gas (bubbles), the perfusion limited compartments would become diffusion limited).
Hennessy concludes that if the undissolved and dissolved gas content of a tissue cannot be independently measured either directly or indirectly then the safe maximum limits relative to the ambient pressure cannot be accurately determined through decompression trials and it will not be possible to systematically develop a comprehensive biophysical model for gas exchange. He proposes a best fit double compartment model for dissolved gas and a single compartment model for undissolved gas as these are the simplest models consistent with available data.[93]
The parameters used in the design of these tables include:[93]
- Bubbles are assumed to form after every decompression.
- These bubbles affect gas uptake and release on repetitive dives, resulting in a faster saturation on repetitive dives due to a combination of redissolved nitrogen from the bubbles, residual dissolved nitrogen, plus the nitrogen uptake due to the repeated exposure.
- Bubbles do not redissolve immediately on recompression, and rates of gas uptake will alter from initial dive to repetitive dives, so repetitive dives must be handled differently in the mathematical model to predict safe decompression.
- Rates of gas elimination are considered to be asymmetric to uptake, and the model becomes more conservative as the number of dives, depth and duration increases.
- The BSAC'88 Tables use a series of seven tables, labelled A to G, to take into account the variation in ingassing and outgassing rates assumed for sequential dives.
- Depth increments of 3 m are used.
- In a significant departure from conventional practice, the tables are not based on a bottom time defined as time of leaving the surface to time leaving the bottom, but on time to reach a depth of 6 m during the ascent.
- Ascent rate to 6 m is restricted to a maximum of 15 m per minute.
- Ascent from 6 m to the surface must take 1 minute.
- Decompression stops are done at 9 m and 6 m, and at the surface, as surface interval is considered a decompression period.
- No stops are scheduled at 3 m, as it is considered too difficult to maintain a consistent depth in waves.
The initial dive uses table A, and the diver is allocated a Surfacing Code based on depth and time of the dive. After a surface interval of at least 15 minutes the diver can select a new Current Tissue Code which models the residual nitrogen load, and uses this code to select the repetitive dive table.[93]
The BSAC'88 tables are presented in a format which does not require any calculation by the user.[92]
Varying Permeability Model
[edit]This decompression model was developed by D.E. Yount and others at the University of Hawaii to model laboratory observations of bubble formation and growth in both inanimate and in vivo systems exposed to pressure variations. It presumes that microscopic bubble nuclei always exist in aqueous media, including living tissues. These bubble nuclei are spherical gas phases that are small enough to remain in suspension yet strong enough to resist collapse, their stability being provided by an elastic surface layer consisting of surface-active molecules with variable gas permeability.[95] These skins resist the effect of surface tension, as surface tension tends to collapse a small bubble by raising internal pressure above ambient so that the partial pressure gradient favours diffusion out of the bubble in inverse proportion to the radius of the surface.[95]
Any nuclei larger than a specific "critical" size, will grow during decompression.[96] The VPM aims to limit the cumulative volume of these growing bubbles during and after decompression to a tolerable level by limiting the pressure difference between the gas in the bubbles and the ambient pressure. In effect, this is equivalent to limiting the supersaturation, but instead of using an arbitrary linear fit to experimental data, the physics of bubble growth is used to model the acceptable supersaturation for any given pressure exposure history.[95]
Growth in size and number of gas bubbles is computed based on factors representing pressure balances in the bubbles, physical properties of the "skins" and the surrounding environment. If the total volume of gas in the bubbles is predicted to be less than a "critical volume", then the diver is assumed to be within the safe limits of the model.[95]
The bubble model is superposed on a multiple parallel tissue compartment model. Ingassing is assumed to follow the classic Haldanean model.[95]
Bubble population distribution
[edit]Bubble size vs number has an exponential distribution[97]
Bubble nucleation
[edit]Gas bubbles with a radius greater than 1 micron should float to the surface of a standing liquid, whereas smaller ones should dissolve rapidly due to surface tension. The Tiny Bubble Group has been able to resolve this apparent paradox by developing and experimentally verifying a new model for stable gas nuclei.[98]
According to the varying-permeability model, gas bubble nuclei are simply stable microbubbles. The stability of these microbubbles is due to elastic skins or membranes consisting of surface-active molecules. These skins are normally permeable to gas, and collapse is prevented by their compression strength. These skins can become stiff and effectively impermeable to gas when they are subjected to large compressions, typically exceeding 8 atm, at which stage the pressure inside increases during further compression as predicted by Boyle's law.[98]
Essentially, there are three parameters in the VP model: the compression strength of the skin; the initial radius; and the onset pressure for impermeability.[98]
Ordering hypothesis
[edit]The ordering hypothesis states that nuclei are neither created nor destroyed by the pressure schedule, and initial ordering according to size is preserved.[99]
It follows from the ordering hypothesis that each bubble count is determined by the properties and behavior of that one "critical" nucleus which is right at the bubble formation threshold. All nuclei that are larger than the critical nucleus will form bubbles, and all nuclei that are smaller will not. Furthermore, a family of pressure schedules which yields the same bubble count N is characterized by the same critical nucleus and hence by the same critical radius, the same crumbling compression, and the same onset of impermeability.[99]
Development of decompression model
[edit]The original assumption was that bubble number is directly proportional to decompression stress. This approach worked well for long exposures, but not when the exposure time varied considerably.[95]
A better model was obtained by allowing more bubbles to form on the shorter dives than on the longer dives. The constant bubble number assumption was replaced by a "dynamic-critical-volume hypothesis". As in earlier applications of the critical-volume criterion,[100] it was assumed that whenever the total volume of gas phase accumulated exceeds a critical value, signs or symptoms of DCS will appear. In the special case of long exposures the two models are equivalent.[101]
The "dynamic" aspect of this hypothesis is that gas is continuously entering and leaving the gas phase.[42]
The accumulated volume is calculated as a function of time by integrating over the product of the bubble number and the degree of supersaturation, and subtracting the free gas that is being dissipated continuously by the lung.[102]
Gas uptake and elimination are assumed to be exponential, as in conventional Haldanean models.[42]
As a first approximation only the inert gasses are taken into account. For oxygen partial pressures above 2.4 bar, the quantity of oxygen dissolved in the arterial blood exceeds the amount that the body can use, and the hemoglobin is saturated with oxygen in both the veins and the arteries. If more oxygen is added, the partial pressure of oxygen in the venous blood rises.[103]
Comparison of VPM profiles with other models
[edit]Comparisons of VPM profiles with USN decompression schedules for extreme exposure dives consistently produce similar total ascent times, but significantly deeper first decompression stops.[101]
Reduced Gradient Bubble Model
[edit]The RGBM developed by Dr Bruce Wienke at Los Alamos National Laboratory is a hybrid model which modifies a Haldanian model with factors to take some account of bubble mechanics to model gas phase production during decompression. The bubble factor modifies the M-values of the Haldanian model, making it more conservative.[104]
Features of the modifying factor ξ include:[104]
- ξ starts on the first dive of a repetitive series with the maximum value of one, so it will make the model more conservative or unchanged.
- ξ decreases for repetitive dives.
- ξ decreases as exposure time increases.
- ξ increases with increased surface interval.
- ξ modifies fast compartments more than slow compartments.
- ξ decreases with the depth of a dive segment
- ξ has more effect on repetitive dives which are deeper than previous dives in the series.
The effect is to reduce no-stop dive time or increase decompression requirements for repetitive dive in the following categories:
- Following a short surface interval.
- Following a long dive.
- Following a deep dive.
- Which are deeper than previous dives.
The model has been used to some extent in some Suunto dive computers,[105] and in the HydroSpace Explorer computer, where it is a user selected option[106] for computation formula, with a choice of additional conservatism factors.
The complete RGBM treats coupled perfusion-diffusion transport as a two-stage process, with perfusion providing a boundary condition for gas penetration of the tissues by diffusion. Either process can dominate the exchange depending on time and rate coefficients.[107]
Simplified implementations which require less computational power are available for use in personal decompression computers. These are dominated by perfusion. The inherent biological unsaturation of tissues is considered in the calculations.[107]
The model assumes that bubble nuclei are always present in a specific size distribution, and that a certain number are induced to grow by compression and decompression. An iterative computation is used to model ascent to limit the combined volume of the gas phase. Gas mixtures of helium, nitrogen, and oxygen contain bubble distributions of different sizes, but the same phase volume limit is used.[108]
The model postulates bubble nuclei with aqueous and/or lipid skin structure, in a number and size distribution quantified by an equation-of-state. Like the VPM, RGBM assumes the size distribution is exponentially decreasing in size. Unlike the varying permeability model, bubble seeds are assumed permeable to gas transfer across skin boundaries under all pressures.[108]
The size of nuclei which will grow during decompression is inversely proportional to the supersaturation gradient.[108]
At higher pressures, skin tension of the bubble nuclei reduces gas diffusion to a slower rate. The model assumes that bubble skins are stabilized by surfactants over calculable times scales, which results in variable persistence of the bubble nuclei in the tissues.[108]
Modifications to models and algorithms for diluent gases other than nitrogen
[edit]Decompression models and algorithms developed for binary mixtures of nitrogen and oxygen can not be used for gases containing significant amounts of other diluent gases without modification to take into account the different solubilities and diffusion constants of the alternative or added diluents. It is also highly desirable to test any such modifications, to make sure the schedules produced by them are acceptably safe.[109][110]
Alternative diluent gases
[edit]- Helium is by far the most important of the alternative diluents used to date.[109][110]
- Hydrogen[111]
- Neon
- Combinations of these gases, particularly the trinary mixtures of helium, nitrogen and oxygen known generically as Trimix.[110]
Decompression models which have been adapted to include alternative and multiple diluents
[edit]Commercial diving tables
[edit]To a large extent commercial offshore diving uses heliox tables that have been developed by the major commercial diving enterprises such as Comex, Oceaneering International (OI) Alpha tables, American Oilfield Diving (AOD) Company gas tables, though modifications of the US Navy Partial pressure tables are also used.[113] In 2006 the unmodified US Navy tables (Revision 5)[clarification needed] were considered to result in an unacceptably high rate of decompression sickness for commercial applications.[113]
"Cx70" heliox tables were developed and used by Comex between 1970 and 1982. The tables were available in two versions. One was designed for surface-supplied diving and limited to 75 m. The diver breathed heliox as the bottom mix and 100% oxygen at the 6 m stop. The other was designed for closed bell bounce diving and allowed for exposures up to 120 minutes, and depths to 120 m. The diver breathed heliox in the water and in the bell, air after transfer into the deck decompression chamber, and finally oxygen on built in breathing system (BIBS) from 12 m to the surface. These tables produced a relatively high incidence of decompression sickness.[83]
The French Tables du Ministère du Travail 1974 (MT74) and Tables du Ministère du Travail 1992 (MT92) were developed specifically for commercial diving.
Norwegian Diving and Treatment Tables, ISBN 82-992411-0-3, referenced in NORSOK Standard U100 2.24 for crewed underwater operations, are available in Norwegian, Danish and English text and are approved for commercial diving.[114]
See also
[edit]- Decompression practice – Techniques and procedures for safe decompression of divers
- Decompression sickness – Disorder caused by dissolved gases forming bubbles in tissues
- Decompression (diving) – Pressure reduction and its effects during ascent from depth
- Decompression theory – Theoretical modelling of decompression physiology
- Equivalent air depth – Method of comparing decompression requirements for air and a given nitrox mix
- Equivalent narcotic depth – Method for comparing the narcotic effects of a mixed diving gas with air
- Hyperbaric treatment schedules – Planned hyperbaric exposure using a specified breathing gas as medical treatment
- List of researchers in diving physiology and medicine
- Oxygen window in diving decompression – Effect of oxygen metabolism on the total dissolved gas concentration in venous blood
- Physiology of decompression – The physiological basis for decompression theory and practice
- Decompression models:
- Bühlmann decompression algorithm – Mathematical model of tissue inert gas uptake and release with pressure change
- Haldane's decompression model – Decompression model developed by John Scott Haldane
- Reduced gradient bubble model – Decompression algorithm
- Thalmann algorithm – Mathematical model for diver decompression
- Thermodynamic model of decompression – Early model in which decompression is controlled by volume of gas bubbles forming in tissues
- Varying Permeability Model – Decompression model and algorithm based on bubble physics
References
[edit]- ^ Hamblyn, Richard (2011). The Art of Science: A Natural History of Ideas. Pan Macmillan. ISBN 9781447204152.
- ^ a b c d e f g Acott, C. (1999). "A brief history of diving and decompression illness". South Pacific Underwater Medicine Society Journal. 29 (2). ISSN 0813-1988. OCLC 16986801.
- ^ a b c Hill, L (1912). Caisson sickness, and the physiology of work in compressed air. London E. Arnold. Retrieved 31 October 2011.
- ^ a b c Huggins 1992, chpt. 1 page 8
- ^ a b c d e Trucco, Jean-Noël; Biard, Jef; Redureau, Jean-Yves; Fauvel, Yvon (3 May 1999). "Table Marine National 90 (MN90): Version du 03/05/1999" (PDF). Comité interrégional Bretagne & Pays de la Loire; Commission Technique Régionale. (in French). F.F.E.S.S.M. Retrieved 23 January 2017.
- ^ Butler, W.P. (2004). "Caisson disease during the construction of the Eads and Brooklyn Bridges: A review". Undersea and Hyperbaric Medicine. 31 (4): 445–59. PMID 15686275.
- ^ Bert, P. (1878). "Barometric Pressure: researches in experimental physiology". Translated by: Hitchcock MA and Hitchcock FA. College Book Company; 1943.
- ^ John L. Phillips, The Bends: Compressed Air in the History of Science, Diving, and Engineering, Yale University Press (1998) - Google Books p 103
- ^ Moon, Richard (March 2000). "The Natural Progression of Decompression Illness and Development of Recompression Procedures". SPUMS Journal. 30 (1): 39.
- ^ N., Zuntz (1897). "Zur Pathogenese und Therapie der durch rasche Luftdruck-änderungen erzeugten Krankheiten". Fortschr, D. Med. (in German). 15: 532–639.
- ^ a b c d e f g h i Boycott, AE; Damant, GCC; Haldane, John Scott (1908). "The Prevention of compressed air illness". Journal of Hygiene. 8 (3): 342–443. doi:10.1017/S0022172400003399. PMC 2167126. PMID 20474365.
- ^ Stillson, G.D. (1915). Report in Deep Diving Tests. US Bureau of Construction and Repair, Navy Department. Technical Report (Report).
- ^ a b c Powell 2008, "Historical perspective"; page 15
- ^ a b c d Huggins 1992, chpt. 3 page 2
- ^ Davis Jefferson C, Sheffield Paul J, Schuknecht L, Heimbach RD, Dunn JM, Douglas G, Anderson GK (August 1977). "Altitude decompression sickness: hyperbaric therapy results in 145 cases". Aviation, Space, and Environmental Medicine. 48 (8): 722–30. PMID 889546.
- ^ Aggazzotti, A.; Ligabue, L. (1942). "Azione dell 'aria compressa sugli animali XX. L'Elasticita di volume del sangue e dei tessuti". Boll. Soc. Ital, Biol. Sper. 17 (479). cited in Beckman 1976
- ^ a b c d Beckman, Edward L. (October 1976). Recommendations for Impmved Air Decompression Schedules for Commercial Diving (PDF). Sea Grant Technical Report UNIHI-SEAGRANT-TR-76-02 (Report). NOAA Office of Sea Grant. Retrieved 3 January 2022.
- ^ Des Granges, M. (1956). Standard air decompression tabLe. Research Report 5-57 (Report). Washington, D.C.: U.S. Navy Experimental Diving Unit.
- ^ Golding, F Campbell; Griffiths, P; Hempleman, H.V.; Paton, W.D.M.; Walder, D.N. (July 1960). "Decompression sickness during construction of the Dartford Tunnel". British Journal of Industrial Medicine. 17 (3): 167–80. doi:10.1136/oem.17.3.167. PMC 1038052. PMID 13850667.
- ^ a b LeMessurier, D. Hugh; Hills, Brian Andrew (1965). "Decompression Sickness. A thermodynamic approach arising from a study on Torres Strait diving techniques". Hvalradets Skrifter (48): 54–84.
- ^ a b Hills, B.A. (1978). "A fundamental approach to the prevention of decompression sickness". South Pacific Underwater Medicine Society Journal. 8 (2).
- ^ How, J.; West, D.; Edmonds, C. (June 1976). "Decompression sickness and diving". Singapore Medical Journal. 17 (22): 92–97. PMID 982095.
- ^ Goodman, M.W.; Workman, R.D. (1965). Minimal-recompression, oxygen-breathing approach to treatment of decompression sickness in divers and aviators. United States Navy Experimental Diving Unit Technical Report (Report). Vol. NEDU-RR-5-65.
- ^ Workman, R.D. (1965). Calculation of decompression schedules for nitrogen-oxygen and helium-oxygen dives. Research Report 6-65 (Report). Washington, D.C: U.S. Navy Experimental Diving Unit. cited by Beckman 1976
- ^ Albano, G.; Columba, M. (1971). "Gas nucleation concept applied to decompression". In Lambertsen, C.J. (ed.). Underwater Physiology. New York: Academic Press. pp. 193–204. cited in Beckman 1976
- ^ Huggins 1992, chpt. 4 page 3
- ^ Graves, D.J.; Idicula, J.; Lambertsen, Christian J.; Quinn, J.A. (March 1973). "Bubble formation resulting from counterdiffusion supersaturation: a possible explanation for isobaric inert gas 'urticaria' and vertigo". Physics in Medicine and Biology. 18 (2): 256–264. Bibcode:1973PMB....18..256G. CiteSeerX 10.1.1.555.429. doi:10.1088/0031-9155/18/2/009. PMID 4805115. S2CID 250737144.
- ^ Graves, DJ; Idicula, J; Lambertsen, Christian J; Quinn, JA (February 1973). "Bubble formation in physical and biological systems: a manifestation of counterdiffusion in composite media". Science. 179 (4073): 582–584. Bibcode:1973Sci...179..582G. doi:10.1126/science.179.4073.582. PMID 4686464. S2CID 46428717.
- ^ a b c d e Imbert, JP; Paris, D.; Hugon, J. (2004). "The Arterial Bubble Model for Decompression Tables Calculations" (PDF). EUBS 2004. France: Divetech. Archived from the original (PDF) on 4 May 2018. Retrieved 4 March 2016.
- ^ Spencer, M.P. (February 1976). "Decompression limits for compressed air determined by ultrasonically detected blood bubbles". Journal of Applied Physiology. 40 (2): 229–35. doi:10.1152/jappl.1976.40.2.229. PMID 1249001.
- ^ a b c d e f Huggins 1992, chpt. 4 page 11
- ^ Yount, D.E. (1981). "Application of bubble formation model to decompression sickness in fingerling salmon". Underwater Biomedical Research. 8 (4). Undersea and Hyperbaric Medical Society, Inc.: 199–208. PMID 7324253.
- ^ Weathersby, Paul K.; Homer, Louis D.; Flynn, Edward T. (September 1984). "On the likelihood of decompression sickness". Journal of Applied Physiology. 57 (3): 815–25. doi:10.1152/jappl.1984.57.3.815. PMID 6490468.
- ^ Thalmann, E.D. (1983). Computer Algorithms Used in Computing the Mk 15/16 Constant 0.7 ATA Oxygen Partial Pressure Decompression Tables. NEDU Report No. 1-83 (Report). Panama City, Florida: Navy Experimental Diving Unit.
- ^ a b c Bühlmann Albert A. (1984). Decompression–Decompression Sickness. Berlin New York: Springer-Verlag. ISBN 978-0-387-13308-9.
- ^ a b c d Huggins 1992, chpt. 4 page 6
- ^ a b Gerth & Doolette 2007, p. 2.
- ^ Thalmann 1985.
- ^ a b c d e f g h i Huggins 1992, chpt. 4 page 10
- ^ Bühlmann, A.A.; Völlm, E.B.; Nussberger, P. (2002). Tauchmedizin (in German). Springer-Verlag. doi:10.1007/978-3-642-55939-6. ISBN 978-3-642-55939-6.
- ^ a b c Yount, D.E.; Hoffman, D.C. (1986). "On the use of a bubble formation model to calculate diving tables". Aviation, Space, and Environmental Medicine. 57 (2): 149–156. ISSN 0095-6562. PMID 3954703.
- ^ a b c "The VPM-B model". V-Planner Deco planning for Technical divers (website). HSS Software Corp. 2015. Retrieved 4 March 2016.
- ^ a b Völlm, Ernst. "Bühlmann algorithm for dive computers" (PDF). Retrieved 29 July 2023.
- ^ a b c d Huggins 1992, chpt. 4 page 4
- ^ a b Travaux en Milieu Hyperbare. Mesures particulières de prévention. Fascicule no 1636. Imprimerie du Journal Officiel, 26 rue Desaix, 75732 Paris cedex 15. ISBN 2-11-073322-5.
- ^ a b Wienke, Bruce R.; O'Leary, Timothy R. (2001). "Full Up Phase Model Decompression Tables". Advanced diver magazine. Retrieved 4 March 2016.
- ^ a b "Decompression Diving". Divetable.de. Retrieved 17 July 2012.
- ^ Gerth & Doolette 2007.
- ^ Goldman, Saul (19 April 2007). "A new class of biophysical models for predicting the probability of decompression sickness in scuba diving". Journal of Applied Physiology. 103 (2): 484–493. doi:10.1152/japplphysiol.00315.2006. PMID 17446410.
- ^ a b US Navy Diving Manual Revision 6
- ^ Huggins 1992, Introduction page 2
- ^ a b Huggins 1992, chpt. 2 page 1
- ^ Huggins 1992, chpt. 2 pages 1–2
- ^ Huggins 1992, chpt. 2 pages 2–3
- ^ Huggins 1992, chpt. 2 pages 3–6
- ^ Huggins 1992, chpt. 3
- ^ Huggins 1992, chpt. 3 page 1
- ^ a b c d e f Huggins 1992, chpt. 3 page 3
- ^ Huggins 1992, chpt. 3 page 4
- ^ Huggins 1992, chpt. 3 page 9
- ^ Huggins 1992, chpt. 3 page 12
- ^ Huggins 1992, chpt. 3 page 13
- ^ a b Huggins 1992, chpt. 4 pages 1–2
- ^ US Navy. US Navy Diving Manual, 5th revision. United States: US Naval Sea Systems Command.
- ^ Huggins 1992, chpt. 4 page 2
- ^ a b Somers, Lee H. (1990). "Chapter 4-2: Introduction to dive tables" (PDF). University of Michigan diving manual. University of Michigan. p. 19. Archived from the original (PDF) on 7 March 2016. Retrieved 7 March 2016.
- ^ a b Huggins 1992, chpt. 4 page 9
- ^ a b c d e Huggins 1992, chpt. 4 page 8
- ^ Somers, Lee H. (1990). "Chapter 4, Appendix B: Introduction to the NAUI dive tables" (PDF). University of Michigan diving manual. Ann Arbor, Michigan: University of Michigan. p. 37. Archived from the original (PDF) on 7 March 2016. Retrieved 7 March 2016.
- ^ Powell 2008, "Other decompression models"; page 213
- ^ a b Huggins 1992, chpt. 4 page 12
- ^ a b c Huggins 1992, chpt. 4 pages 12–13
- ^ a b Huggins 1992, chpt. 4 pages 2–3
- ^ a b Nishi, Ronald; Lauchner, G. (1984). Development of the DCIEM 1983 Decompression Model for Compressed Air Diving. Defence and Civil Institute of Environmental Medicine Technical Report (Report). Vol. DCIEM-84–R-44.
- ^ Mesures particulières de protection applicables aux scaphandriers. Fascicule Spécial no 74-48 bis. Bulletin Officiel du Ministère du travail. Imprimerie du Journal Officiel, 26 rue Desaix, 75732 Paris cedex 15.
- ^ Imbert, J.P.; Bontoux, M. (12 September 1986). Safety analysis of French 1974 air decompression tables. Proceedings of the Undersea Medical Society Workshop on Decompression in surface-based diving. Tokyo, Japan.
- ^ Imbert, J.P.; Bontoux, M. (13–14 February 1987). A method for introducing new decompression procedures. Proceedings of the Undersea Medical Society Workshop on validation of decompression schedules. Bethesda, Maryland.
- ^ a b Imbert, J. P. (August 2008). "28: Arterial Bubble Model". In Mount, Tom; Dituri, Joseph (eds.). Exploration and Mixed Gas Diving Encyclopedia (1st ed.). Miami Shores, Florida: International Association of Nitrox Divers. pp. 315–320. ISBN 978-0-915539-10-9.
- ^ Balestra, C.; Germonpre, P.; Marroni, A. (1998). "Intrathoracic pressure changes after Valsalva strain and other maneuvers: implication for divers with patent foramen ovale". Undersea Hyperb. Med. 25 (3): 171–4. PMID 9789337.
- ^ Germonpre, P.; et al. (1988). "Patent foramen ovale and decompression sickness in sport divers". J. Appl. Physiol. 84 (5): 1622–6. doi:10.1152/jappl.1998.84.5.1622. PMID 9572808.
- ^ Imbert, J.P. (20 September – 3 October 1991). Decompression tables versus decompression procedures: an analysis of decompression sickness using diving data-bases. Proceedings of the XVIIth annual meeting of Diving and Hyperbaric Medicine. Heraklion, Crete, Greece.
- ^ a b c Imbert, Jean Pierre (February 2006). Lang; Smith (eds.). "Commercial Diving: 90m Operational Aspects" (PDF). Advanced Scientific Diving Workshop. Retrieved 30 June 2012.
- ^ a b Parker et al. 1992, p. 1
- ^ Thalmann 1984, abstract
- ^ Huggins 1992, chpt. 4 page 13
- ^ Thalmann 1985, p. 6
- ^ Parker et al. 1992, p. 3
- ^ Gerth & Doolette 2007, p. 1.
- ^ Ball 1995, p. 272.
- ^ Ball 1995, p. 273.
- ^ a b c "BSAC 88 Decompression Tables – British Sub-Aqua Club". Bsac.com. Retrieved 17 July 2012.
- ^ a b c d Lippmann 1990, pp. 325–328
- ^ Hennessy, T.R. (1988). "Modelling human exposure to altered pressure environments.". In Mekjavik, I.B.; Banister, E.W.; Morrison, J.B. (eds.). Environmental Ergonomics. London: Taylor & Francis. pp. 316 to 331.
- ^ a b c d e f Yount 1991.
- ^ Wienke, Bruce (March 1992). "Modeling phase volume constraints under repetitive decompression". Mathematical and Computer Modelling. 16 (3): 109–120. doi:10.1016/0895-7177(92)90052-M.
- ^ Yount 1991, p. 136.
- ^ a b c Yount 1991, p. 131.
- ^ a b Yount 1991, p. 132.
- ^ Hennessy, T. R.; Hempleman, H. V. (1977). "An examination of the critical released gas volume concept in decompression sickness". Proceedings of the Royal Society of London. Series B. 197 (1128): 299–313. Bibcode:1977RSPSB.197..299H. doi:10.1098/rspb.1977.0072. PMID 19749. S2CID 6692808.
- ^ a b Yount 1991, p. 138.
- ^ Yount 1991, p. 137.
- ^ Yount, D. E. and D. A. Lally. 1980. On the use of oxygen to facilitate decompression. Aviation, Space, and Environmental Medicine, 51: 544–550.
- ^ a b Huggins 1992, chpt. 4 page 14
- ^ "Suunto Reduced Gradient Bubble Model" (PDF). suunto_brochure.qxd 24 July 2003 11:53 Sivu 3. Suunto. 2003. Retrieved 4 March 2016.
- ^ a b c "HS Explorer Dive Computer Owner's Manual". HSE website. St. Augustine, FL: HydroSpace Engineering, Inc. 2003. Archived from the original on 4 March 2016. Retrieved 4 March 2016.
- ^ a b Wienke 2002, p. 10
- ^ a b c d Wienke 2002, p. 11
- ^ a b Gernhardt, M.L. (2006). Biomedical and Operational Considerations for Surface-Supplied Mixed-Gas Diving to 300 FSW. In: Lang, MA and Smith, NE (eds.). Proceedings of Advanced Scientific Diving Workshop (Report). Washington, DC.: Smithsonian Institution. p. 44.
- ^ a b c Doolette DJ, Gault KA, Gerth WA (2015). "Decompression from He-N2-O2 (trimix) bounce dives is not more efficient than from He-O2 (heliox) bounce dives". US Navy Experimental Diving Unit Technical Report 15-4.
- ^ Brauer, R.W. (1985). Hydrogen as a Diving Gas. 33rd Undersea and Hyperbaric Medical Society Workshop (Report). Bethesda: Undersea and Hyperbaric Medical Society.
- ^ "V-Planner VPM & VPM-B & VPMB & VPM-B/E dive decompression software". Hhssoftware.com. Retrieved 17 July 2012.
- ^ a b Beyerstein, Gary (2006). Commercial Diving: Surface-Mixed Gas, Sur-D-O2, Bell Bounce, Saturation (Report). New Orleans, La.
- ^ NORSOK STANDARD U-100, Edition 3. Manned underwater operations. (Report). Lysaker: Standards Norway. April 2009. ISBN 978-8299241106. Retrieved 4 March 2016.
Sources
[edit]- Ball, R.; Himm, J.; Homer, L.D.; Thalmann, E.D (1995). "Does the time course of bubble evolution explain decompression sickness risk?". Undersea and Hyperbaric Medicine. 22 (3): 263–280. ISSN 1066-2936. PMID 7580767.
- Gerth, Wayne A.; Doolette, David J. (2007). "VVal-18 and VVal-18M Thalmann Algorithm – Air Decompression Tables and Procedures". Navy Experimental Diving Unit, TA 01-07, NEDU TR 07-09.
- Huggins, Karl E. (1992). "Dynamics of decompression workshop". Course Taught at the University of Michigan.
- Lippmann, John (1990). Deeper into Diving (1st ed.). Melbourne, Australia: J L Publications. ISBN 978-0-9590306-3-1.
- Parker, E.C.; Survanshi, S.S.; Weathersby, P.K.; Thalmann, E.D. (1992). "Statistically Based Decompression Tables VIII: Linear Exponential Kinetics". Naval Medical Research Institute Report. 92–73.
- Powell, Mark (2008). Deco for Divers. Southend-on-Sea: Aquapress. ISBN 978-1-905492-07-7.
- Thalmann, E.D. (1984). Phase II testing of decompression algorithms for use in the U.S. Navy underwater decompression computer. Navy Exp. Diving Unit Res. Report (Report). Vol. 1–84.
- Thalmann, E.D. (1985). Development of a Decompression Algorithm for Constant Oxygen Partial Pressure in Helium Diving. Navy Exp. Diving Unit Res. Report (Report). Vol. 1–85.
- US Navy (2008). US Navy Diving Manual, 6th revision. United States: US Naval Sea Systems Command. Retrieved 15 June 2008.
- Wienke, Bruce R; O'Leary, Timothy R (13 February 2002). "Reduced gradient bubble model: Diving algorithm, basis and comparisons" (PDF). Tampa, Florida: NAUI Technical Diving Operations. Retrieved 25 January 2012.
- Yount, D.E. (1991). Hans-Jurgen, K; Harper Jr, D.E. (eds.). Gelatin, bubbles, and the bends. Proceedings of the American Academy of Underwater Sciences Eleventh Annual Scientific Diving Symposium, 25–30 September 1991 (Report). University of Hawaii, Honolulu, Hawaii): International Pacifica Scientific Diving...
Other reading
[edit]- Brubakk, A.O.; Neuman, T.S. (2003). Bennett and Elliott's physiology and medicine of diving (5th Revised ed.). United States: Saunders. ISBN 978-0-7020-2571-6.
- Hamilton, Robert W.; Thalmann, Edward D. (2003). "10.2: Decompression Practice". In Brubakk, Alf O.; Neuman, Tom S. (eds.). Bennett and Elliott's physiology and medicine of diving (5th Revised ed.). United States: Saunders. pp. 455–500. ISBN 978-0-7020-2571-6. OCLC 51607923.
- Elliott, David (4 December 1998). "Decompression theory in 30 minutes". SPUMS Journal. 28 (4): 206–214.