| ||||
|---|---|---|---|---|
| Cardinal | eight | |||
| Ordinal | 8th (eighth) | |||
| Numeral system | octal | |||
| Factorization | 23 | |||
| Divisors | 1, 2, 4, 8 | |||
| Greek numeral | Η´ | |||
| Roman numeral | VIII, viii | |||
| Greek prefix | octa-/oct- | |||
| Latin prefix | octo-/oct- | |||
| Binary | 10002 | |||
| Ternary | 223 | |||
| Senary | 126 | |||
| Octal | 108 | |||
| Duodecimal | 812 | |||
| Hexadecimal | 816 | |||
| Greek | η (or Η) | |||
| Arabic, Kurdish, Persian, Sindhi, Urdu | ٨ | |||
| Amharic | ፰ | |||
| Bengali | ৮ | |||
| Chinese numeral | 八,捌 | |||
| Devanāgarī | ८ | |||
| Kannada | ೮ | |||
| Malayalam | ൮ | |||
| Telugu | ౮ | |||
| Tamil | ௮ | |||
| Hebrew | ח | |||
| Khmer | ៨ | |||
| Thai | ๘ | |||
| Armenian | Ը ը | |||
| Babylonian numeral | 𒐜 | |||
| Egyptian hieroglyph | 𓐁 | |||
| Morse code | _ _ _.. | |||
8 (eight) is the natural number following 7 and preceding 9.
Etymology
[edit]English eight, from Old English eahta, æhta, Proto-Germanic *ahto is a direct continuation of Proto-Indo-European *oḱtṓ(w)-, and as such cognate with Greek ὀκτώ and Latin octo-, both of which stems are reflected by the English prefix oct(o)-, as in the ordinal adjective octaval or octavary, the distributive adjective is octonary. The adjective octuple (Latin octu-plus) may also be used as a noun, meaning "a set of eight items"; the diminutive octuplet is mostly used to refer to eight siblings delivered in one birth.
The Semitic numeral is based on a root *θmn-, whence Akkadian smn-, Arabic ṯmn-, Hebrew šmn- etc. The Chinese numeral, written 八 (Mandarin: bā; Cantonese: baat), is from Old Chinese *priāt-, ultimately from Sino-Tibetan b-r-gyat or b-g-ryat which also yielded Tibetan brgyat.
It has been argued that, as the cardinal number 7 is the highest number of items that can universally be cognitively processed as a single set, the etymology of the numeral eight might be the first to be considered composite, either as "twice four" or as "two short of ten", or similar. The Turkic words for "eight" are from a Proto-Turkic stem *sekiz, which has been suggested as originating as a negation of eki "two", as in "without two fingers" (i.e., "two short of ten; two fingers are not being held up");[1] this same principle is found in Finnic *kakte-ksa, which conveys a meaning of "two before (ten)". The Proto-Indo-European reconstruction *oḱtṓ(w)- itself has been argued as representing an old dual, which would correspond to an original meaning of "twice four". Proponents of this "quaternary hypothesis" adduce the numeral 9, which might be built on the stem new-, meaning "new" (indicating the beginning of a "new set of numerals" after having counted to eight).[2]
Evolution of the Arabic digit
[edit]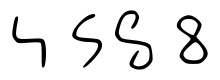
The modern digit 8, like all modern Arabic numerals other than zero, originates with the Brahmi numerals. The Brahmi digit for eight by the 1st century was written in one stroke as a curve └┐ looking like an uppercase H with the bottom half of the left line and the upper half of the right line removed. However, the digit for eight used in India in the early centuries of the Common Era developed considerable graphic variation, and in some cases took the shape of a single wedge, which was adopted into the Perso-Arabic tradition as ٨ (and also gave rise to the later Devanagari form ८); the alternative curved glyph also existed as a variant in Perso-Arabic tradition, where it came to look similar to our digit 5.[year needed]
The digits as used in Al-Andalus by the 10th century were a distinctive western variant of the glyphs used in the Arabic-speaking world, known as ghubār numerals (ghubār translating to "sand table"). In these digits, the line of the 5-like glyph used in Indian manuscripts for eight came to be formed in ghubār as a closed loop, which was the 8-shape that became adopted into European use in the 10th century.[3]
Just as in most modern typefaces, in typefaces with text figures the character for the digit 8 usually has an ascender, as, for example, in ![]() .
.
The infinity symbol ∞, described as a "sideways figure eight", is unrelated to the digit 8 in origin; it is first used (in the mathematical meaning "infinity") in the 17th century, and it may be derived from the Roman numeral for "one thousand" CIƆ, or alternatively from the final Greek letter, ω.
Mathematics
[edit]Eight is the third composite number, lying between the fourth prime number (7) and the fourth composite number (9). 8 is the first non-unitary cube prime of the form p3. With proper divisors 1, 2, and 4, it is the third power of two (23). 8 is the first number which is neither prime nor semiprime and the only nonzero perfect power that is one less than another perfect power, by Mihăilescu's Theorem.
- 8 is the first proper Leyland number of the form xy + yx, where in its case x and y both equal 2.[4]
- 8 is the sum between the first pair of twin-primes (3, 5), and the only twin-prime sum that is not a multiple of 3 or 12.
- 8 is the sixth Fibonacci number and the first even, non-prime Fibonacci number. It is also the only positive Fibonacci number aside from 1 that is a perfect cube.[5]
- 8 is the third refactorable number, as it has exactly four positive divisors, and 4 is one of them.
- 8 is the only composite number with a prime aliquot sum of 7 (1 + 2 + 4)[6] that is part of the aliquot sequence (8, 7, 1, 0).
- 8 is the first number to be the aliquot sum of two numbers: the discrete semiprime 10 = 5 × 2, and squared prime 49 = 72.
- 8 is surrounded by (7, 9) which multiply to equal the forty-fourth composite number 63,[7] where the eighth triangular number and twenty-fourth composite is 36.[8]
- 8 is the number of known primary pseudoperfect numbers,[9] the smallest four (2, 6, 42, 1806) are one less than the first four numbers in Sylvester's sequence.
Sphenic numbers always have exactly eight divisors.[10]
Octagon
[edit]A polygon with eight sides is an octagon.[11] The sides and span of a regular octagon, or truncated square, are in 1 : 1 + √2 silver ratio, and its circumscribing square has a side and diagonal length ratio of 1 : √2; with both the silver ratio and the square root of two intimately interconnected through Pell numbers, where in particular the quotient of successive Pell numbers generates rational approximations for coordinates of a regular octagon.[12][13] With a central angle of 45 degrees and an internal angle of 135 degrees, a regular octagon can fill a plane-vertex with a regular triangle and a regular icositetragon, as well as tessellate two-dimensional space alongside squares in the truncated square tiling. This tiling is one of eight Archimedean tilings that are semi-regular, or made of more than one type of regular polygon, and the only tiling that can admit a regular octagon.[14] The Ammann–Beenker tiling is a nonperiodic tesselation of prototiles that feature prominent octagonal silver eightfold symmetry, that is the two-dimensional orthographic projection of the four-dimensional 8-8 duoprism.[15] In number theory, figurate numbers representing octagons are called octagonal numbers.[16]
Cube and octahedron
[edit]A cube is a regular polyhedron with eight vertices that also forms the cubic honeycomb, the only regular honeycomb in three-dimensional space.[17] Through various truncation operations, the cubic honeycomb generates eight other convex uniform honeycombs under the cubic group .[18] The octahedron, with eight equilateral triangles as faces, is the dual polyhedron to the cube and one of eight convex deltahedra.[19][20] The stella octangula, or eight-pointed star, is the only stellation with octahedral symmetry. It has eight triangular faces alongside eight vertices that forms a cubic faceting, composed of two self-dual tetrahedra that makes it the simplest of five regular compounds. The cuboctahedron, on the other hand, is a rectified cube or rectified octahedron, and one of only two convex quasiregular polyhedra. It contains eight equilateral triangular faces, whose first stellation is the cube-octahedron compound.[21][22] There are also eight uniform polyhedron compounds made purely of octahedra, including the regular compound of five octahedra, and an infinite amount of polyhedron compounds made only of octahedra as triangular antiprisms (UC22 and UC23, with p = 3 and q = 1).
- Truncated figures
The truncated tetrahedron is the simplest Archimedean solid, made of four triangles and four hexagons, the hexagonal prism, which classifies as an irregular octahedron and parallelohedron, is able to tessellate space as a three-dimensional analogue of the hexagon, and the gyrobifastigium, with four square faces and four triangular faces, is the only Johnson solid that is able to tessellate space. The truncated octahedron, also a parallelohedron, is the permutohedron of order four, with eight hexagonal faces alongside six squares is likewise the only Archimedean solid that can generate a honeycomb on its own.
Polychora
[edit]A tesseract or 8-cell is the four-dimensional analogue of the cube. It is one of six regular polychora, with a total of eight cubical cells, hence its name. Its dual figure is the analogue of the octahedron, with twice the amount of cells and simply termed the 16-cell, that is the orthonormal basis of vectors in four dimensions. Whereas a tesseractic honeycomb is self-dual, a 16-cell honeycomb is dual to a 24-cell honeycomb that is made of 24-cells. The 24-cell is also regular, and made purely of octahedra whose vertex arrangement represents the ring of Hurwitz integral quaternions. Both the tesseract and the 16-cell can fit inside a 24-cell, and in a 24-cell honeycomb, eight 24-cells meet at a vertex. Also, the Petrie polygon of the tesseract and the 16-cell is a regular octagon.
The octonions
[edit]The octonions are a hypercomplex normed division algebra that are an extension of the complex numbers. They are realized in eight dimensions, where they have an isotopy group over the real numbers that is spin group Spin(8), the unique such group that exhibits a phenomenon of triality. As a double cover of special orthogonal group SO(8), Spin(8) contains the special orthogonal Lie algebra D4 as its Dynkin diagram, whose order-three outer automorphism is isomorphic to the symmetric group S3, giving rise to its triality. Over finite fields, the eight-dimensional Steinberg group 3D4(q3) is simple, and one of sixteen such groups in the classification of finite simple groups. As is Lie algebra E8, whose complex form in 248 dimensions is the largest of five exceptional Lie algebras that include E7 and E6, which are held inside E8. The smallest such algebra is G2, that is the automorphism group of the octonions. In mathematical physics, special unitary group SO(3) has an eight-dimensional adjoint representation whose colors are ascribed gauge symmetries that represent the vectors of the eight gluons in the Standard Model.
The number 8 is involved with a number of interesting mathematical phenomena related to the notion of Bott periodicity. If is the direct limit of the inclusions of real orthogonal groups , the following holds:
- .
Clifford algebras also display a periodicity of 8.[23] For example, the algebra Cl(p + 8,q) is isomorphic to the algebra of 16 by 16 matrices with entries in Cl(p,q). We also see a period of 8 in the K-theory of spheres and in the representation theory of the rotation groups, the latter giving rise to the 8 by 8 spinorial chessboard. All of these properties (that also tie with Lorentzian geometry, and Jordan algebras) are closely related to the properties of the octonions, which occupy the highest possible dimension for a normed division algebra.
E8
[edit]The lattice Γ8 is the smallest positive even unimodular lattice. As a lattice, it holds the optimal structure for the densest packing of 240 spheres in eight dimensions, whose lattice points also represent the root system of Lie group E8. This honeycomb arrangement is shared by a unique complex tessellation of Witting polytopes, also with 240 vertices. Each complex Witting polytope is made of Hessian polyhedral cells that have Möbius–Kantor polygons as faces, each with eight vertices and eight complex equilateral triangles as edges, whose Petrie polygons form regular octagons. In general, positive even unimodular lattices only exist in dimensions proportional to eight. In the 16th dimension, there are two such lattices : Γ8 ⊕ Γ8 and Γ16, while in the 24th dimension there are precisely twenty-four such lattices that are called the Niemeier lattices, the most important being the Leech lattice, which can be constructed using the octonions as well as with three copies of the ring of icosians that are isomorphic to the lattice.[24][25] The order of the smallest non-abelian group all of whose subgroups are normal is 8.
Vertex-transitive semiregular polytopes whose facets are finite exist up through the 8th dimension. In the third dimension, they include the Archimedean solids and the infinite family of uniform prisms and antiprisms, while in the fourth dimension, only the rectified 5-cell, the rectified 600-cell, and the snub 24-cell are semiregular polytopes. For dimensions five through eight, the demipenteract and the k21 polytopes 221, 321, and 421 are the only semiregular (Gosset) polytopes. Collectively, the k21 family of polytopes contains eight figures that are rooted in the triangular prism, which is the simplest semiregular polytope that is made of three cubes and two equilateral triangles. It also includes one of only three semiregular Euclidean honeycombs: the affine 521 honeycomb that represents the arrangement of vertices of the eight-dimensional lattice, and made of 421 facets. The culminating figure is the ninth-dimensional 621 honeycomb, which is the only affine semiregular paracompact hyperbolic honeycomb with infinite facets and vertex figures in the k21 family. There are no other finite semiregular polytopes or honeycombs in dimensions n > 8.
Finite simple groups
[edit]In the classification of sporadic groups, the third generation consists of eight groups, four of which are centralizers of (itself the largest group of this generation), with another three transpositions of Fischer group .[26] 8 is the difference between 53 and 61, which are the two smallest prime numbers that do not divide the order of any sporadic group. The largest supersingular prime that divides the order of is 71, which is the eighth self-convolution of Fibonacci numbers (where 744, which is essential to Moonshine theory, is the twelfth).[27][28] While only two sporadic groups have eight prime factors in their order (Lyons group and Fischer group ), Mathieu group holds a semi-presentation whose order is equal to .[29]
List of basic calculations
[edit]| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 × x | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 | 104 | 112 | 120 |
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8 ÷ x | 8 | 4 | 2.6 | 2 | 1.6 | 1.3 | 1.142857 | 1 | 0.8 | 0.8 | 0.72 | 0.6 | 0.615384 | 0.571428 | 0.53 | |
| x ÷ 8 | 0.125 | 0.25 | 0.375 | 0.5 | 0.625 | 0.75 | 0.875 | 1 | 1.125 | 1.25 | 1.375 | 1.5 | 1.625 | 1.75 | 1.875 |
| Exponentiation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 8x | 8 | 64 | 512 | 4096 | 32768 | 262144 | 2097152 | 16777216 | 134217728 | 1073741824 | 8589934592 | 68719476736 | 549755813888 | |
| x8 | 1 | 256 | 6561 | 65536 | 390625 | 1679616 | 5764801 | 16777216 | 43046721 | 100000000 | 214358881 | 429981696 | 815730721 |
In other bases
[edit]A number is divisible by 8 if its last three digits, when written in decimal, are also divisible by 8, or its last three digits are 0 when written in binary.
8 is the base of the octal number system, which is mostly used with computers.[30] In octal, one digit represents three bits. In modern computers, a byte is a grouping of eight bits, also called an octet.
In science
[edit]Physics
[edit]- In nuclear physics, the second magic number.[31]
- In particle physics, the eightfold way is used to classify sub-atomic particles.[32]
- In statistical mechanics, the eight-vertex model has 8 possible configurations of arrows at each vertex.[33]
Astronomy
[edit]- Messier object M8, a magnitude 5.0 nebula in the constellation of Sagittarius.[34]
- The New General Catalogue object NGC 8, a double star in the constellation Pegasus.
- Since the demotion of Pluto to a dwarf planet on 24 August 2006, in our Solar System, eight of the bodies orbiting the Sun are considered to be planets.
Chemistry
[edit]- The atomic number of oxygen.[35]
- The most stable allotrope of a sulfur molecule is made of eight sulfur atoms arranged in a rhombic form.[36]
- The maximum number of electrons that can occupy a valence shell (except for transitional elements), see the octet rule.
- The red pigment lycopene consists of eight isoprene units.[37]
Geology
[edit]- A disphenoid crystal is bounded by eight scalene triangles arranged in pairs. A ditetragonal prism in the tetragonal crystal system has eight similar faces whose alternate interfacial angles only are equal.
Biology
[edit]- All spiders, and more generally all arachnids, have eight legs.[38] Orb-weaver spiders of the cosmopolitan family Areneidae have eight similar eyes.[39]
- The octopus and its cephalopod relatives in genus Argonauta have eight arms (tentacles).
- Compound coelenterates of the subclass or order Alcyonaria have polyps with eight-branched tentacles and eight septa.[40]
- Sea anemones of genus Edwardsia have eight mesenteries.[41]
- Animals of phylum Ctenophora swim by means of eight meridional bands of transverse ciliated plates, each plate representing a row of large modified cilia.[42]
- The eight-spotted forester (genus Alypia, family Zygaenidae) is a diurnal moth having black wings with brilliant white spots.
- The ascus in fungi of the class Ascomycetes, following nuclear fusion, bears within it typically eight ascospores.[43]
- Herbs of genus Coreopsis (tickseed) have showy flower heads with involucral bracts in two distinct series of eight each.
- In human adult dentition there are eight teeth in each quadrant.[44] The eighth tooth is the so-called wisdom tooth.
- There are eight cervical nerves on each side in man and most mammals.[45]
Psychology
[edit]- There are eight Jungian cognitive functions, according to the MBTI models by John Beebe and Linda Berens.[46]
- Timothy Leary identified a hierarchy of eight levels of consciousness.
In technology
[edit]
- A byte is eight bits.[47]
- Many (mostly historic) computer architectures are eight-bit, among them the Nintendo Entertainment System.
- Standard-8 and Super-8 are 8 mm film formats.[48]
- Video8, Hi8 and Digital8 are related 8 mm video formats.[49]
- On most phones, the 8 key is associated with the letters T, U, and V, but on the BlackBerry Pearl it is the key for B and N.
- An eight may refer to an eight-cylinder engine or automobile.[50] A V8 engine is an internal combustion engine with eight cylinders configured in two banks (rows) of four forming a "V" when seen from the end.
- A figure-eight knot (so named for its configuration) is a kind of stopper knot.[51]
- The number eight written in parentheses is the code for the musical note in Windows Live Messenger.
- In a seven-segment display, when an 8 is illuminated, all the display bulbs are on.
In measurement
[edit]- The SI prefix for 10008 is yotta (Y), and for its reciprocal, yocto (y).
- In liquid measurement (United States customary units), there are eight fluid ounces in a cup, eight pints in a gallon and eight tablespoonfuls in a gill.[52]
- There are eight furlongs in a mile.[53]
- The clove, an old English unit of weight, was equal to eight pounds when measuring cheese.[54]
- An eight may be an article of clothing of the eighth size.
- Force eight is the first wind strength attributed to a gale on the Beaufort scale when announced on a Shipping Forecast.[55]
In culture
[edit]Currency
[edit]- Sailors and civilians alike from the 1500s onward referred to evenly divided parts of the Spanish dollar as "pieces of eight", or "bits".
Architecture
[edit]- Various types of buildings are usually eight-sided (octagonal), such as single-roomed gazebos[56] and multi-roomed pagodas (descended from stupas; see religion section below).
- Eight caulicoles rise out of the leafage in a Corinthian capital, ending in leaves that support the volutes.
In religion, folk belief and divination
[edit]Hinduism
[edit]- As sourced from the Mahabharata, there are 8 vasus who are given elemental names:[57]
- Anala or Agni (fire)
- Dhara or Prithvi (earth)
- Anila or Vayudeva (wind)
- Apa (water)
- Prabhasa or Dyauh (sky)
- Pratyusha
- Soma
- Dhruva
- The goddess of wealth and prosperity, Lakshmi, has eight forms known as Ashta Lakshmi and worshipped as:
"Maha-lakshmi, Dhana-lakshmi, Dhanya-lakshmi, Gaja-lakshmi,
Santana-lakshmi, Veera-lakshmi, Vijaya-lakshmi and Vidhya-lakshmi"[58] - There are eight nidhi, or seats of wealth, according to Hinduism.
- There are eight guardians of the directions known as Astha-dikpalas.[59]
- There are eight Hindu monasteries established by the saint Madhvacharya in Udupi, India popularly known as the Ashta Mathas of Udupi.[60]
Buddhism
[edit]
- The Dharmacakra, a Buddhist symbol, has eight spokes.[61] The Buddha's principal teaching—the Four Noble Truths—ramifies as the Noble Eightfold Path and the Buddha emphasizes the importance of the eight attainments or jhanas.
- In Mahayana Buddhism, the branches of the Eightfold Path are embodied by the Eight Great Bodhisattvas: (Manjusri, Vajrapani, Avalokiteśvara, Maitreya, Ksitigarbha, Nivaranavishkambhi, Akasagarbha, and Samantabhadra).[62] These are later (controversially) associated with the Eight Consciousnesses according to the Yogacara school of thought: consciousness in the five senses, thought-consciousness, self-consciousness, and unconsciousness-"consciousness" or "store-house consciousness" (alaya-vijñana). The "irreversible" state of enlightenment, at which point a Bodhisattva goes on "autopilot", is the Eight Ground or bhūmi. In general, "eight" seems to be an auspicious number for Buddhists, e.g., the "eight auspicious symbols" (the jewel-encrusted parasol; the goldfish (always shown as a pair, e.g., the glyph of Pisces); the self-replenishing amphora; the white kamala lotus-flower; the white conch; the eternal (Celtic-style, infinitely looping) knot; the banner of imperial victory; the eight-spoked wheel that guides the ship of state, or that symbolizes the Buddha's teaching). Similarly, Buddha's birthday falls on the 8th day of the 4th month of the Chinese calendar.
Judaism
[edit]- The religious rite of brit milah (commonly known as circumcision) is held on a baby boy's eighth day of life.[63]
- Hanukkah is an eight-day Jewish holiday that starts on the 25th day of Kislev.[64]
- Shemini Atzeret (Hebrew: "Eighth Day of Assembly") is a one-day Jewish holiday immediately following the seven-day holiday of Sukkot.[65]
Christianity
[edit]- The spiritual Eighth Day, because the number 7 refers to the days of the week (which repeat themselves).
- The number of Beatitudes.[66]
- 1 Peter 3:20 states that there were eight people on Noah's Ark.[67]
- The Antichrist is the eighth king in the Book of Revelation.[68]
Islam
[edit]
- In Islam, eight is the number of angels carrying the throne of Allah in heaven.[69]
- The number of gates of heaven.[70]
- The octagram Rub el Hizb is often used in Islamic symbology.
Taoism
[edit]Other
[edit]- In Wicca, there are eight Sabbats, festivals, seasons, or spokes in the Wheel of the Year.[73]
- In Ancient Egyptian mythology, the Ogdoad represents the eight primordial deities of creation.[74]
- In Scientology there are eight dynamics of existence.[75]: 39
- There is also the Ogdoad in Gnosticism.[76]
As a lucky number
[edit]- The number eight is considered to be a lucky number in Chinese and other Asian cultures.[77] Eight (八; accounting 捌; pinyin bā) is considered a lucky number in Chinese culture because it sounds like the word meaning to generate wealth (發(T) 发(S); Pinyin: fā). Property with the number 8 may be valued greatly by Chinese. For example, a Hong Kong number plate with the number 8 was sold for $640,000.[78] The opening ceremony of the Summer Olympics in Beijing started at 8 seconds and 8 minutes past 8 pm (local time) on 8 August 2008.[79]
- In Pythagorean numerology the number 8 represents victory, prosperity and overcoming.
- Eight (八, hachi, ya) is also considered a lucky number in Japan, but the reason is different from that in Chinese culture.[80] Eight gives an idea of growing prosperous, because the letter (八) broadens gradually.
- The Japanese thought of eight (や, ya) as a holy number in the ancient times. The reason is less well-understood, but it is thought that it is related to the fact they used eight to express large numbers vaguely such as manyfold (やえはたえ, Yae Hatae) (literally, eightfold and twentyfold), many clouds (やくも, Yakumo) (literally, eight clouds), millions and millions of Gods (やおよろずのかみ, Yaoyorozu no Kami) (literally, eight millions of Gods), etc. It is also guessed that the ancient Japanese gave importance to pairs, so some researchers guess twice as four (よ, yo), which is also guessed to be a holy number in those times because it indicates the world (north, south, east, and west) might be considered a very holy number.
- In numerology, 8 is the number of building, and in some theories, also the number of destruction.
In astrology
[edit]- In astrology, Scorpio is the 8th astrological sign of the Zodiac.[81]
- In the Middle Ages, 8 was the number of "unmoving" stars in the sky, and symbolized the perfection of incoming planetary energy.
In music and dance
[edit]- A note played for one-eighth the duration of a whole note is called an eighth note, or quaver.[82]
- An octave, the interval between two musical notes with the same letter name (where one has double the frequency of the other), is so called because there are eight notes between the two on a standard major or minor diatonic scale, including the notes themselves and without chromatic deviation.[83] The ecclesiastical modes are ascending diatonic musical scales of eight notes or tones comprising an octave.
- There are eight notes in the octatonic scale.
- There are eight musicians in a double quartet or an octet.[84] Both terms may also refer to a musical composition for eight voices or instruments.[85]
- Caledonians is a square dance for eight, resembling the quadrille.
- Albums with the number eight in their title include 8 by the Swedish band Arvingarna, 8 by the American rock band Incubus,[86] The Meaning of 8 by Minnesota indie rock band Cloud Cult and 8ight by Anglo-American singer-songwriter Beatie Wolfe.[87]
- Dream Theater's eighth album Octavarium contains many different references to the number 8, including the number of songs and various aspects of the music and cover artwork.
- "Eight maids a-milking" is the gift on the eighth day of Christmas in the carol "The Twelve Days of Christmas".[88]
- The 8-track cartridge is a musical recording format.
- "#8" is the stage name of Slipknot vocalist Corey Taylor.
- "Too Many Eights" is a song by Athens, Georgia's Supercluster.[89]
- Eight Seconds, a Canadian musical group popular in the 1980s with their most notable song "Kiss You (When It's Dangerous)".[90]
- "Eight Days a Week" is a #1 single for the music group the Beatles.[91]
- Figure 8 is the fifth studio album by singer-songwriter Elliott Smith, released in the year 2000,[92] an album released by Julia Darling in 1999,[93] and an album released by Outasight in 2011.[94]
- Ming Hao from the k-pop group Seventeen goes by the name "The8".[95]
- "8 (circle)" is the eighth song on the album 22, A Million by the American band Bon Iver.[96]
- "8" is the eighth song on the album When We All Fall Asleep, Where Do We Go? by Billie Eilish.[97]
In film and television
[edit]- 8 Guys is a 2003 short film written and directed by Dane Cook.
- 8 Man (or Eightman): 1963 Japanese manga and anime superhero.
- 8 Mile is a 2002 film directed by Curtis Hanson.[98]
- 8 mm is a 1999 film directed by Joel Schumacher.[99]
- 8 Women (Original French title: 8 femmes) is a 2001 film directed by François Ozon.[100]
- Eight Below is a 2006 film directed by Frank Marshall.[101]
- Eight Legged Freaks is a 2002 film directed by Ellory Elkayem.[102]
- Eight Men Out is a 1988 film directed by John Sayles.[103]
- Jennifer Eight, also known as Jennifer 8, is a 1992 film written and directed by Bruce Robinson.[104]
- Eight Is Enough is an American television comedy-drama series.
- In Stargate SG-1 and Stargate Atlantis, dialing an 8-chevron address will open a wormhole to another galaxy.
- The Hateful Eight is a 2015 American western mystery film written and directed by Quentin Tarantino.[105]
- Kate Plus 8 is an American reality television show.[106]
- Ocean's 8 is an American heist comedy film directed by Gary Ross.[107]
In sports and other games
[edit]
- Eight-ball pool is played with a cue ball and 15 numbered balls, the black ball numbered 8 being the middle and most important one, as the winner is the player or side that legally pockets it after first pocketing its numerical group of 7 object balls (for other meanings see Eight ball (disambiguation)).
- In chess, each side has eight pawns and the board is made of 64 squares arranged in an eight by eight lattice. The eight queens puzzle is a challenge to arrange eight queens on the board so that none can capture any of the others.
- In the game of eights or Crazy Eights, each successive player must play a card either of the same suit or of the same rank as that played by the preceding player, or may play an eight and call for any suit. The object is to get rid of all one's cards first.
- In association football, the number 8 has historically been the number of the Central Midfielder.
- In Australian rules football, the top eight teams at the end of the Australian Football League regular season qualify for the finals series (i.e. playoffs).
- In baseball:
- The center fielder is designated as number 8 for scorekeeping purposes.
- The Men's College World Series, the final phase of the NCAA Division I tournament, features eight teams.
- In rugby union, the only position without a proper name is the Number 8, a forward position.
- In rugby league:
- Most competitions (though not the Super League, which uses static squad numbering) use a position-based player numbering system in which one of the two starting props wears the number 8.
- The Australia-based National Rugby League has its own 8-team finals series, similar but not identical in structure to that of the Australian Football League.
- In rowing, an "eight" refers to a sweep-oar racing boat with a crew of eight rowers plus a coxswain.[108]
- In the 2008 Games of the XXIX Olympiad held in Beijing, the official opening was on 08/08/08 at 8:08:08 p.m. CST.
- In rock climbing, climbers frequently use the figure-eight knot to tie into their harnesses.
- The Women's College World Series, the final phase of the NCAA Division I softball tournament, like its men's counterpart in baseball, features eight teams.
- In curling an 8-point 'Eight Ender' is a perfect end. Each team delivers 8 Stones per end.
In foods
[edit]- Nestlé sells a brand of chocolates filled with peppermint-flavoured cream called After Eight, referring to the time 8 p.m.[109]
- There are eight vegetables in V8 juice.[110]
In literature
[edit]- Eights may refer to octosyllabic, usually iambic, lines of verse.
- The drott-kvaett, an Old Icelandic verse, consisted of a stanza of eight regular lines.[111]
- In Terry Pratchett's Discworld series, eight is a magical number[112] and is considered taboo. Eight is not safe to be said by wizards on the Discworld and is the number of Bel-Shamharoth. Also, there are eight days in a Disc week and eight colours in a Disc spectrum, the eighth one being octarine.
- Lewis Carroll's poem The Hunting of the Snark has 8 "fits" (cantos), which is noted in the full name "The Hunting of the Snark – An Agony, in Eight Fits".[113]
- Eight apparitions appear to Macbeth in Act 4 scene 1 of Shakespeare's Macbeth as representations of the eight descendants of Banquo.
In slang
[edit]- An "eighth" is a common measurement of marijuana, meaning an eighth of an ounce. It is also a common unit of sale for psilocybin mushrooms.[114]
- Avril Lavigne's song "Sk8er Boi" uses this convention in the title.
- The Housing Choice Voucher Program, operated by the United States Department of Housing and Urban Development, is commonly referred to as the Section 8 program, as this was the original section of the Act which instituted the program.[115]
- In Colombia and Venezuela, "volverse un ocho" (meaning to tie oneself in a figure 8) refers to getting in trouble or contradicting oneself.
- In China, "8" is used in chat speak as a term for parting. This is due to the closeness in pronunciation of "8" (bā) and the English word "bye".
Other uses
[edit]- A figure 8 is the common name of a geometric shape, often used in the context of sports, such as skating.[116] Figure-eight turns of a rope or cable around a cleat, pin, or bitt are used to belay something.[117]
See also
[edit]References
[edit]- ^ Etymological Dictionary of Turkic Languages: Common Turkic and Interturkic stems starting with letters «L», «M», «N», «P», «S», Vostochnaja Literatura RAS, 2003, 241f. (altaica.ru Archived 31 October 2007 at the Wayback Machine)
- ^ the hypothesis is discussed critically (and rejected as "without sufficient support") by Werner Winter, 'Some thought about Indo-European numerals' in: Jadranka Gvozdanović (ed.), Indo-European Numerals, Walter de Gruyter, 1992, 14f.
- ^ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 395, Fig. 24.68.
- ^ Sloane, N. J. A. (ed.). "Sequence A076980 (Leyland numbers)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation.
- ^ Bryan Bunch, The Kingdom of Infinite Number. New York: W. H. Freeman & Company (2000): 88
- ^ Sloane, N. J. A. (ed.). "Sequence A001065 (Sum of proper divisors (or aliquot parts) of n: sum of divisors of n that are less than n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 8 August 2023.
- ^ Sloane, N. J. A. (ed.). "Sequence A002808 (The composite numbersnumbers n of the form x*y for x > 1 and y > 1.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 24 September 2023.
- ^ Sloane, N. J. A. (ed.). "Sequence A000217 (Triangular numbers: a(n) is the binomial(n+1,2) equal to n*(n+1)/2 and 0 + 1 + 2 + ... + n)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 24 September 2023.
- ^ Sloane, N. J. A. (ed.). "Sequence A054377 (Primary pseudoperfect numbers: numbers n > 1 such that 1/n + sum 1/p is 1, where the sum is over the primes p | n.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 11 January 2024.
- ^ Weisstein, Eric W. "Sphenic Number". mathworld.wolfram.com. Retrieved 7 August 2020.
...then every sphenic number n=pqr has precisely eight positive divisors
- ^ Weisstein, Eric W. "Octagon". mathworld.wolfram.com. Retrieved 7 August 2020.
- ^ Bicknell, Marjorie (1975). "A primer on the Pell sequence and related sequences". Fibonacci Quarterly. 13 (4): 345–349. MR 0387173.
- ^ Knuth, Donald E. (1994). "Leaper graphs". The Mathematical Gazette. 78 (483): 283. arXiv:math.CO/9411240. Bibcode:1994math.....11240K. doi:10.2307/3620202. JSTOR 3620202. S2CID 16856513.
- ^ Weisstein, Eric W. "Regular Octagon". mathworld.wolfram.com. Retrieved 25 June 2022.
- ^ Katz, A (1995). "Matching rules and quasiperiodicity: the octagonal tilings". In Axel, F.; Gratias, D. (eds.). Beyond quasicrystals. Springer. pp. 141–189. doi:10.1007/978-3-662-03130-8_6. ISBN 978-3-540-59251-8.
- ^ Deza, Elena; Deza, Michel (2012). Figurate Numbers. World Scientific. pp. 39, 40, 92, 151. ISBN 9789814355483..
- ^ Weisstein, Eric W. "Cube". mathworld.wolfram.com. Retrieved 7 August 2020.
- ^ Branko Grünbaum (1994). "Uniform tilings of 3-space". Geombinatorics. 4 (2): 49–56.
- ^ Freudenthal, H; van der Waerden, B. L. (1947), "Over een bewering van Euclides ("On an Assertion of Euclid")", Simon Stevin (in Dutch), 25: 115–128
- ^ Roger Kaufman. "The Convex Deltahedra And the Allowance of Coplanar Faces". The Kaufman Website. Retrieved 25 June 2022.
- ^ Weisstein, Eric W. "Cuboctahedron". mathworld.wolfram.com. Retrieved 25 June 2022.
- ^ Coxeter, H.S.M. (1973) [1948]. Regular Polytopes (3rd ed.). New York: Dover. pp. 18–19.
- ^ Lounesto, Pertti (3 May 2001). Clifford Algebras and Spinors. Cambridge University Press. p. 216. ISBN 978-0-521-00551-7.
...Clifford algebras, contains or continues with two kinds of periodicities of 8...
- ^ Wilson, Robert A. (2009). "Octonions and the Leech lattice". Journal of Algebra. 322 (6): 2186–2190. doi:10.1016/j.jalgebra.2009.03.021. MR 2542837.
- ^ Conway, John H.; Sloane, N. J. A. (1988). "Algebraic Constructions for Lattices". Sphere Packings, Lattices and Groups. New York, NY: Springer. doi:10.1007/978-1-4757-2016-7. eISSN 2196-9701. ISBN 978-1-4757-2016-7.
- ^ Griess, Jr., Robert L. (1998). Twelve Sporadic Groups. Springer Monographs in Mathematics. Berlin: Springer-Verlag. pp. 146−150. ISBN 9783540627784. MR 1707296. OCLC 38910263. Zbl 0908.20007.
- ^ Moree, Pieter (2004). "Convoluted Convolved Fibonacci Numbers" (PDF). Journal of Integer Sequences. 7 (2). Waterloo, Ont., CA: University of Waterloo David R. Cheriton School of Computer Science: 13 (Article 04.2.2). arXiv:math.CO/0311205. Bibcode:2004JIntS...7...22M. MR 2084694. S2CID 14126332. Zbl 1069.11004.
- ^ Sloane, N. J. A. (ed.). "Sequence A001629 (Self-convolution of Fibonacci numbers.)". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 16 July 2023.
- ^ Wilson, R.A.; Parker, R.A.; et al. (1999). "ATLAS: Mathieu group M23". ATLAS of Finite Group Representations.
- ^ Weisstein, Eric W. "Octal". mathworld.wolfram.com. Retrieved 7 August 2020.
- ^ Ilangovan, K. (10 June 2019). Nuclear Physics. MJP Publisher. p. 30.
- ^ Gell-Mann, M. (15 March 1961). THE EIGHTFOLD WAY: A THEORY OF STRONG INTERACTION SYMMETRY (Technical report). OSTI 4008239.
- ^ Baxter, R. J. (5 April 1971). "Eight-Vertex Model in Lattice Statistics". Physical Review Letters. 26 (14): 832–833. Bibcode:1971PhRvL..26..832B. doi:10.1103/PhysRevLett.26.832.
- ^ "Messier Object 8". www.messier.seds.org. Retrieved 7 August 2020.
- ^ Thomas, Mary Ann (15 August 2004). Oxygen. The Rosen Publishing Group, Inc. p. 12. ISBN 978-1-4042-0159-0.
Knowing that oxygen has an atomic number of 8,
- ^ Choppin, Gregory R.; Johnsen, Russell H. (1972). Introductory chemistry. Addison-Wesley Pub. Co. p. 366. ISBN 978-0-201-01022-0.
under normal conditions the most stable allotropic form (Fig. 23-8a). Sulfur molecules within the crystal consist of puckered rings of eight sulfur atoms linked by single...
- ^ Puri, Basant; Hall, Anne (16 December 1998). Phytochemical Dictionary: A Handbook of Bioactive Compounds from Plants, Second Edition. CRC Press. p. 810. ISBN 978-0-203-48375-6.
The chemical structure of lycopene consists of a long chain of eight isoprene units joined head to tail
- ^ Parker, Barbara Keevil (28 December 2006). Ticks. Lerner Publications. p. 7. ISBN 978-0-8225-6464-5.
Arachnids have eight legs
- ^ Jackman, J. A. (1997). A Field Guide to Spiders & Scorpions of Texas. Gulf Publishing Company. p. 70. ISBN 978-0-87719-264-0.
Araneids have eight eyes
- ^ Fisher, James; Huxley, Julian (1961). The Doubleday Pictorial Library of Nature: Earth, Plants, Animals. Doubleday. p. 311.
Polyps with eight branched tentacles and eight septa
- ^ Bourne, Gilbert Charles (1911). . In Chisholm, Hugh (ed.). Encyclopædia Britannica. Vol. 02 (11th ed.). Cambridge University Press. pp. 97–105, see page 100.
Zoantharia.....It is not known whether all the eight mesenteries of Edwardsia are developed simultaneously or not, but in the youngest form which has been studied all the eight mesenteries were present
- ^ The Century Dictionary and Cyclopedia: A work of Universal Reference in all Departments of Knowledge with a New Atlas of the World. 1906. p. 1384.
...are radially symmetrical, and swim by means of eight meridional ciliated bands, ...
- ^ Parrish, Fred K. (1975). Keys to Water Quality Indicative Organisms of the Southeastern United States. Environmental Protection Agency, Office of Research and Development, Environmental Monitoring and Support Laboratory, Biological Methods Branch, Aquatics Biology Section. p. 11.
... the ascospores, are borne in sac like structures termed asci. The ascus usually contains eight as cospores,...
- ^ Dofka, Charline M. (1996). Competency Skills for the Dental Assistant. Cengage Learning. p. 83. ISBN 978-0-8273-6685-5.
...In each quadrant of the permanent set of teeth (dentition), there are eight teeth
- ^ Quain, Jones (1909). Quain's Elements of Anatomy. Longmans, Green, & Company. p. 52.
These eight pairs are usually reckoned as eight cervical nerves ...
- ^ Beebe, John (17 June 2016). Energies and Patterns in Psychological Type: The reservoir of consciousness. Routledge. p. 124. ISBN 978-1-317-41366-0.
Linda Berens used the term 'cognitive processes' (1999) to refer to the eight types of consciousness that Jung discovered.
- ^ "Definition of byte | Dictionary.com". www.dictionary.com. Retrieved 8 August 2020.
- ^ Kindem, Gorham; PhD, Robert B. Musburger (21 August 2012). Introduction to Media Production: The Path to Digital Media Production. CRC Press. p. 320. ISBN 978-1-136-05322-1.
There used to be two 8 mm formats: standard 8 mm and Super-8 mm.
- ^ The Library of Congress Veterans History Project: Field Kit : Conducting and Preserving Interviews. Veterans History Project, American Folklife Center, Library of Congress. 2008. p. 15.
Betacam SX 8 mm Hi8, Digital8, Video8 DVD-Video";
- ^ "Definition of eight | Dictionary.com". www.dictionary.com. Retrieved 8 August 2020.
- ^ Griffiths, Garth (1971). Boating in Canada: Practical Piloting and Seamanship. University of Toronto Press. p. 32. ISBN 978-0-8020-1817-5.
First is a stopper knot, the figure of eight, ...
- ^ The Milwaukee Cook Book. Press of Houtkamp Printing. 1907.
- ^ "Definition of furlong | Dictionary.com". www.dictionary.com. Retrieved 8 August 2020.
- ^ "Definition of clove | Dictionary.com". www.dictionary.com. Retrieved 8 August 2020.
- ^ Fairhall, David; Peyton, Mike (17 May 2013). Pass Your Yachtmaster. A&C Black. ISBN 978-1-4081-5627-8.
Gale warnings will be given if mean wind speeds of force 8 (34–40 knots)
- ^ Sayers, William (2003). "Eastern Prospects: Kiosks, Belvederes, Gazebos". Neophilologus. 87 (2): 299–305. doi:10.1023/A:1022691123957. S2CID 159542713.
- ^ "Who are the eight vasus?". Hinduism Stack Exchange. Retrieved 19 December 2023.
- ^ Hatcher, Brian A. (5 October 2015). Hinduism in the Modern World. Routledge. ISBN 978-1-135-04630-9.
a group manifestation of eight forms
- ^ Jeyaraj, Daniel (23 September 2004). Genealogy of the South Indian Deities: An English Translation of Bartholomäus Ziegenbalg's Original German Manuscript with a Textual Analysis and Glossary. Routledge. p. 168. ISBN 978-1-134-28703-1.
He is one of the eight guardians of the world
- ^ Ramachandran, Nirmala (2000). Hindu Heritage. Stamford Lake Publication. p. 72. ISBN 978-955-8733-09-7.
The temple has eight monasteries, founded by Madhvacharya
- ^ Issitt, Micah; Main, Carlyn (16 September 2014). Hidden Religion: The Greatest Mysteries and Symbols of the World's Religious Beliefs: The Greatest Mysteries and Symbols of the World's Religious Beliefs. ABC-CLIO. p. 186. ISBN 978-1-61069-478-0.
The dharmachakra is typically depicted with eight spokes,
- ^ Hay, Jeff (6 March 2009). World Religions. Greenhaven Publishing LLC. p. 61. ISBN 978-0-7377-4627-3.
The focus of ordinary believers' religious life is on following a relevant version of the Eightfold Path ...
- ^ Rosten, Leo (14 April 2010). The New Joys of Yiddish: Completely Updated. Potter/Ten Speed/Harmony/Rodale. p. 48. ISBN 978-0-307-56604-1.
Brit Milah is observed on a boy's eighth day of life
- ^ Ross, Kathy (1 August 2012). Crafts for Hanukkah. Millbrook Press. p. 7. ISBN 978-0-7613-6836-6.
Hanukkah is an eight-day Jewish holiday
- ^ Axelrod, Cantor Matt (24 December 2013). Your Guide to the Jewish Holidays: From Shofar to Seder. Rowman & Littlefield. p. 58. ISBN 978-0-7657-0990-5.
Shemini Atzeret—literally, "the eighth day of assembly"
- ^ "CATHOLIC ENCYCLOPEDIA: The Eight Beatitudes". www.newadvent.org. Retrieved 9 August 2020.
- ^ Akintola, Olufolahan Olatoye (2011). Nations of the World…How They Evolved!: Families and Nations That Came Out of Ham. Hilldew View International Limited. p. 8. ISBN 978-0-9569702-2-0.
These eight souls in Noah's ark were the survivors...
- ^ Livingstone (2001). Life Application New Testament Commentary. Tyndale House Publishers, Inc. ISBN 978-0-8423-7066-0.
- ^ Mahmutćehajić, Rusmir (2011). Maintaining the Sacred Center: The Bosnian City of Stolac. World Wisdom, Inc. p. 201. ISBN 978-1-935493-91-4.
... at the last, eight Angels will carry the Throne...
- ^ "Names of the Gates of Heaven". islamweb.net. Retrieved 19 December 2023.
- ^ Little, Stephen; Eichman, Shawn; Shipper, Kristofer; Ebrey, Patricia Buckley (1 January 2000). Taoism and the Arts of China. University of California Press. p. 139. ISBN 978-0-520-22785-9.
Evidence for the early use of the Eight Trigrams in a religious Taoist...
- ^ Ho, Peter Kwok Man; Kwok, Man-Ho; O'Brien, Joanne (1990). The Eight Immortals of Taoism: Legends and Fables of Popular Taoism. Meridian. p. 7. ISBN 978-0-452-01070-3.
...famous Eight Immortals of China...
- ^ Zimmermann, Denise; Gleason, Katherine; Liguana, Miria (2006). The Complete Idiot's Guide to Wicca and Witchcraft. Penguin. p. 172. ISBN 978-1-59257-533-6.
There are eight Sabbats
- ^ Remler, Pat (2010). Egyptian Mythology, A to Z. Infobase Publishing. p. 79. ISBN 978-1-4381-3180-1.
...of the gods of the Ogdoad, or the eight deities of the Egyptian creation...
- ^ Wallis, Roy (1977). The Road to Total Freedom: A Sociological Analysis of Scientology. Columbia University Press. ISBN 0231042000. OL 4596322M.
- ^ David, Fideler (1993). Jesus Christ, Sun of God: Ancient Cosmology and Early Christian Symbolism. Quest Books. p. 128. ISBN 978-0-8356-0696-7.
- ^ Ang, Swee Hoon (1997). "Chinese consumers' perception of alpha-numeric brand names". Journal of Consumer Marketing. 14 (3): 220–233. doi:10.1108/07363769710166800. Archived from the original on 5 December 2011.
- ^ Steven C. Bourassa; Vincent S. Peng (1999). "Hedonic Prices and House Numbers: The Influence of Feng Shui" (PDF). International Real Estate Review. 2 (1): 79–93. Archived from the original (PDF) on 13 April 2015. Retrieved 11 May 2011.
- ^ "Olympics opening ceremony: China makes its point with greatestshow". the Guardian. 8 August 2008. Retrieved 29 November 2022.
- ^ Jefkins, Frank (6 December 2012). Modern Marketing Communications. Springer Science & Business Media. p. 36. ISBN 978-94-011-6868-7.
...eight being a lucky number in Japanese.
- ^ "Definition of SCORPIO". www.merriam-webster.com. Retrieved 10 August 2020.
- ^ "Definition of eighth note | Dictionary.com". www.dictionary.com. Retrieved 9 August 2020.
- ^ "Definition of OCTAVE". www.merriam-webster.com. Retrieved 9 August 2020.
a tone or note that is eight steps above or below another note or tone
- ^ "Definition of octet | Dictionary.com". www.dictionary.com. Retrieved 9 August 2020.
a company of eight singers or musicians.
- ^ "Definition of octet | Dictionary.com". www.dictionary.com. Retrieved 9 August 2020.
a musical composition for eight voices or instruments.
- ^ "Incubus Premiere New Song "Glitterbomb", Detail New Album "8"". Theprp.com. 17 March 2017. Retrieved 9 August 2020.
- ^ Beatie Wolfe-8ight, retrieved 9 August 2020
- ^ Tribble, Mimi (2004). 300 Ways to Make the Best Christmas Ever!: Decorations, Carols, Crafts & Recipes for Every Kind of Christmas Tradition. Sterling Publishing Company, Inc. ISBN 978-1-4027-1685-0.
- ^ Too Many Eights – Supercluster | Song Info | AllMusic, retrieved 10 August 2020
- ^ "Eight Seconds | Biography & History". AllMusic. Retrieved 10 August 2020.
- ^ Eight Days a Week – The Beatles | Song Info | AllMusic, retrieved 10 August 2020
- ^ Figure 8 – Elliott Smith | Songs, Reviews, Credits | AllMusic, retrieved 10 August 2020
- ^ Figure 8 – Julia Darling | Songs, Reviews, Credits | AllMusic, retrieved 10 August 2020
- ^ Figure 8 – Outasight | Songs, Reviews, Credits | AllMusic, retrieved 10 August 2020
- ^ "The8 | Credits". AllMusic. Retrieved 10 August 2020.
- ^ 22, A Million – Bon Iver | Songs, Reviews, Credits | AllMusic, retrieved 10 August 2020
- ^ When We All Fall Asleep, Where Do We Go? - Billie Eilish | Songs, Reviews, Credits | AllMusic, retrieved 10 August 2020
- ^ 8 Mile (2002) – Curtis Hanson | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ 8MM (1999) – Joel Schumacher | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ 8 Women (2001) – François Ozon | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Eight Below (2006) – Bruce Hendricks, Frank Marshall | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Eight Legged Freaks (2002) – Ellory Elkayem | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Eight Men Out (1988) – John Sayles | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Jennifer Eight (1992) – Bruce Robinson | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ The Hateful Eight (2015) – Quentin Tarantino | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Jon & Kate Plus 8 (2007) - | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 10 August 2020
- ^ Ocean's 8 (2018) – Sandra Bullock | Synopsis, Characteristics, Moods, Themes and Related | AllMovie, retrieved 13 January 2023
- ^ "Definition of EIGHT". www.merriam-webster.com. Retrieved 10 August 2020.
- ^ "Buy After Eight® Online | Nestlé Family ME". www.nestle-family.com. Retrieved 10 August 2020.
- ^ "V8® Vegetable Juice Ingredients". V8® Fruit and Vegetable Juices. Retrieved 19 December 2023.
- ^ "Definition of DROTT-KVAETT". www.merriam-webster.com. Retrieved 10 August 2020.
- ^ Collins, Robert; Latham, Robert (1988). Science Fiction & Fantasy Book Review Annual. Meckler. p. 289. ISBN 978-0-88736-249-1.
- ^ "The Hunting of the Snark". www.gutenberg.org. Retrieved 10 August 2020.
- ^ Franciosi, Anthony (25 October 2019). "Weed Measurements: The Marijuana Metric System". Honest Marijuana. Retrieved 19 December 2023.
- ^ "CT Housing Choice Voucher Program". www.cthcvp.org. Retrieved 11 August 2020.
Welcome to the Housing Choice Voucher Program (also known as Section 8)
- ^ Boys' Life. Boy Scouts of America, Inc. 1931. p. 20.
lunge forward upon this skate in a left outside forward circle, in just the reverse of your right outside forward circle, until you complete a figure 8.
- ^ Day, Cyrus Lawrence (1986). The Art of Knotting & Splicing. Naval Institute Press. p. 231. ISBN 978-0-87021-062-4.
To make a line temporarily fast by winding it, figure – eight fashion, round a cleat, a belaying pin, or a pair of bitts.
External links
[edit]- The Octonions, John C. Baez
|










